Алгоритм это набор инструкций описывающих порядок действий

Что такое алгоритм?! Часть первая

Терзаем вместе основной кирпичик программиста — Алгоритм.

Проблема

Текущее состояние в области программирования — это обучение ремеслу по большей части личной практикой или разборами примеров стороннего кода, с которым по каким-то причинам приходится сталкиваться.

В результате программированию учишься по наитию. Лишь немного в этом труде помогают сборники алгоритмов, прикладных техник и шаблонов проектирования. Общая совокупность предлагаемых ими рецептов выстраивается длинным списком, и его длина грозит каждому из прочитанных приемов быть позабытым (как была забыта 53-яя личная группа в «телеге» до введения разбиения по каталогам). Но даже тот прием, который остался в памяти, чаще всего просто является описанием прикладной задачи, в которой было успешно его использование.

Почему конкретный прием был успешен в задаче-образце? Будет ли он успешен в твоём проекте? Какие признаки проекта дают понять, что использование приёма уместно?

В личном опыте существования в профессии не раз отмечено, что каждый Junior борется с одинаковыми ветряными мельницами и постигает методы создания программ основываясь только на своих ошибках. Но ведь такие ошибки совершили уже очень многие. Почему до сих пор не создана система правил программирования, которая поможет обойти новоиспеченному кораблю-программисту подводные прибрежные камни? Ну, например, объяснение вреда использования метода «Copy-Paste» для развития кода. Если такие правила получится объяснить малым набором причин, их сформировавшим, то это объяснение обеспечит их запоминание и последующее использование в практике, тем самым поможет уклониться от бесчисленных грабель, разложенных тут и там.

Для компактного и полезного набора объяснений нужно:

• систематизировать методы работы с кодом;
• разобрать по группам приёмы работы с алгоритмами, которые являются главной целью написания любого кода;
• выделить простые признаки применения шаблонов проектирования;
• разработать универсальные правила и наборы эффективных способов построения сложных алгоритмов.

Если обобщить, то нужны алгоритмы для написания и развития алгоритмов.

Задуманная серия статей не претендует на полное решение указанной проблемы. Предпринимается небесспорная попытка сделать первый шаг на пути к этому решению. Этот шаг состоит в выделении структуры и свойств главного кирпичика программиста — Алгоритма.

Задача

Сформулируем основную задачу, которую хочется решить. Для этого сначала запишем операции над алгоритмами, которые программист выполняет в ходе написания своего проекта:

• методы синтеза макро-алгоритма из под-алгоритмов (последовательной, параллельной и смешанной группировкой);
• методы структурной трансформации макро-алгоритмов (оптимизационной, специализирующей, стыковочной…);
• методы сохранения и переноса алгоритмов;
• методы синтеза универсального алгоритма из сходных алгоритмов разных областей исполнения;
• методы специализации универсального алгоритма в новой области исполнения;
• методы формирования и развития комплексной системы совместно работающих алгоритмов;
• методы взаимодействия одновременно исполняющихся алгоритмов;
• и другие методы, полный список которых привести сложно, да и нет необходимости.

Рассмотрим существующие на текущий момент варианты значения слова «алгоритм» в поисках подсказок, о том как можно работать с алгоритмами.

Так, например, формулировка «конечная совокупность точно заданных правил решения произвольного класса задач» говорит что есть возможность как-то «точно задать правила» из них собрать «совокупность» и этой совокупностью «решить» некоторый «класс задач».

Сразу возникает масса вопросов к этому определению:

• Что такое правило?
• Как, кому и для кого это правило можно задать?
• Что есть объединение совокупностью?
• Каким образом правила соотносятся с задачей?
• Что формирует класс задачи?
• Определяется ли способ формирования совокупности правилами и задачами?
• …

Другая формулировка «набор инструкций, описывающих порядок действий исполнителя для решения некоторой задачи» говорит что есть «исполнитель», который может выполнять некоторые «действия», и при некотором «порядке» выполнения этих «действий» «решается задача». Вопросов не стало меньше:

• Какова структура набора?
• Какие есть варианты действий и исполнителей?
• Существуют ли минимально возможное действие, минимальный набор необходимых действий?
• Каким образом действия встроены в исполнителя?
• Какие есть способы создания копии исполнителя (например, если исполнитель — человек)?
• Как действия зависят друг от друга в упорядоченном выполнении?
• Что есть задача кроме того, что она выполняется последовательностью действий?
• Как задача соотносится с исполнителем и с действиями?
• Возможно ли использовать решение задачи в качестве действия?
• Какие возможны варианты указания порядка действий?
• Если воспроизведение патефоном записи звуков леса является алгоритмом, то какова структура этой задачи?
• Если репликация ДНК является алгоритмом, то каков её исполнитель?
• Если исполнителем является Машина Тьюринга, то как с её использованием решить механическую задачу, например, воспроизведение звука?

Перечислено много вопросов, но они мало помогают в поиске методов работы с алгоритмом. Поэтому поставим себе меньшую задачу, но тоже очень нам важную. Давайте попробуем сформулировать, что делает алгоритм способом решения наших задач, и какие процессы являются для него «действиями». Даже решение этой «маленькой» задачи оказывается очень объемным для одной статьи, поэтому будем его разбивать на части. И поэтому первую статью серии целиком посвятим только «Действию» и его признакам, которые опущены в указанных выше определениях алгоритма, но являются очень важными для ответов на все заданные вопросы.

Определение алгоритма

Рассмотрим определение алгоритма, говорящее, что он — приводящая к решению задачи последовательность действий. Как программисту мне приходится писать много кода. Этот код состоит из частей. Такими частями являются и функции, и классы, и модули. Когда я пишу текст функции — я занимаюсь написанием алгоритма.

Раньше алгоритм создавали в виде блок схем и полуавтоматически компилировали в машинные коды. Сейчас я избавлен от необходимости быть художником и компилятором для написания программы. Текст моей функции — это запись алгоритма в текстовом виде — его текстовая блок-схема. Здесь можно вспомнить Scratch, где используется визуальное создание блок-схемы алгоритма без написания текста. Способ записи алгоритма сейчас не так важен.

Важно, что в написании алгоритма функции я могу использовать вызовы других функции, которые я или другой программист уже написал до этого момента. Вспоминая фразу «последовательность действий, приводящая к решению задачи», можно отметить, что функции, написанные ранее, являются моими «действиями». То есть «действия» могут быть функциями. Если обобщать, то «действия» могут быть алгоритмами.

Если «действие = алгоритм», то определение можно попробовать переписать рекурсивно «алгоритм — это приводящая к решению задачи последовательность использования существующих алгоритмов». Рекурсивные определение не самое простое, что можно записать в словаре обычного человека. Но для программиста и математика эта форма знакома. Мы умеем с ней работать, и это даёт нам преимущество в рассмотрении разных задач, разбиваемых на подобные себе подзадачи. Так давайте воспользуемся этим преимуществом.

Чтобы разрешить рекурсию нам необходимо найти:

• терминальное условие выхода из рекурсии — минимальное неделимое «действие» (атомарный алгоритм), которое можно использовать в разработке алгоритма;
• способ перехода от текущего уровня рекурсии (набора «действий») к следующему уровню (алгоритму).

Действие

Для начала рассмотрим «действие» и попробуем найти причину, обеспечивающую возможность использования существующего «действия» для создания нового алгоритма.

Этой причиной является возможность повторного использования «действия» с получением тождественного результата. Только тогда разработанный с использованием этого «действия» алгоритм решения некоторой задачи будет одинаково решать эту задачу снова и снова. Мы нащупали важные законы нашего мира, в котором:

• существуют «действия», главным свойством которых является одинаковость результатов их исполнения в разные моменты времени и в разных местах,
• существует возможность создать такую схему использования нескольких «действий», которая сформирует из них новое «действие», которое мы назвали алгоритмом.

Какие признаки «действия» кроме повторимости делают возможным его использование в создании алгоритма? Что является терминальным неделимым «действием»? Чтобы ответить на этот вопрос стоит рассмотреть разные примеры «действий» из нашего опыта. Программисты встречали их много раз. Это и сложение, и умножение, и установка цвета пикселя на экране. Но мы знакомы с ними и вне программирования. Вся наука основывается на повторяемых явлениях.

Закон гравитации, описывающий повторяющееся явление падения яблока, тоже может стать действием. Ведь любое яблоко будет падать на землю? Значит этот процесс можно использовать в качестве «действия»! Например решая задачу прогнать Ньютона от яблони, на которую Вы случайно забрались ранее.

Рассмотрим, что происходит при выполнении «действия». Например, во время падения яблока с ветки яблони на землю. В этом процессе происходит несколько изменений. Если вспомнить школьную физику и рассмотреть ситуацию в системе отсчета, привязанной к Земле, то сила гравитации вызывает изменение скорости яблока, разгоняя его. При этом в процессе отмечается еще одно важное изменение — уменьшается расстояние между яблоком и Землей.

В рамках примера процесса «Земля-Яблоко» можно отметить у «действия» следующие признаки:

• наличие процесса изменения (расстояния и параметров движения объектов);
• наличие объектов, взаимодействие которых вызывает такие изменения;
• наличие локальности процесса, то есть существование значения расстояния между объектами, с превышением которого их взаимодействие перестает вызывать процесс изменения, что делает невозможным использование «действия» (Земля и гипотетическое яблоко, находящееся вне солнечной системы).

Рассмотрим с этими признаками разные области и процессы, выделяя в них примеры «действий» и контролируя особенности указанных признаков в описании структуры «действия».

Физические процессы

Для физических систем, процессы которых мы наблюдаем в нашем мире, характерные объекты и изменения опираются на фундаментальные взаимодействия и потому их достаточно просто выделить по аналогии с гравитационным взаимодействием Земли и яблока. Например, для системы из протона и электрона или системы двух протонов.

Отдельно от этих простых взаимодействий двух объектов стоят многокомпонентные процессы, например, ядерные реакции (по структуре «действия» близки к химическим процессам, рассматриваемым далее). Сложны и процессы описываемые суммарным взаимодействием большого числа элементов, например, «идеальный газ». Пока отложим их рассмотрение и сосредоточимся на самых простых примерах.

Химические процессы

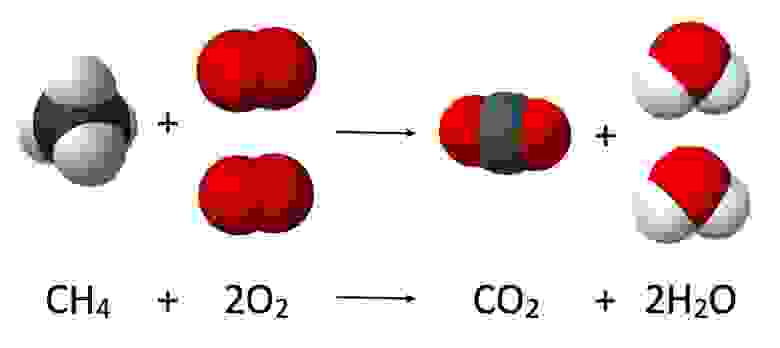
Перейдем к следующей большой области — химическим процессам. Химические реакции (например, ) по признаку своей повторимости так же являются «действиями». Объектами в них являются атомы и молекулы. Для описания происходящих изменений необходимо немного преобразовать «физические» изменения. Так изменения параметров движения в совокупности дают нам изменение температуры в ходе химической реакции. А среди изменений расстояний между молекулами мы, игнорируя броуновское движение, можем выделить фиксацию расстояния в виде повторимого формирования и разрушения связей между частями взаимодействующих молекул. Локальность для химической реакции тоже существует — это отсутствие реакции при нахождении гидроксида натрия и соляной кислоты в разных пробирках и наличие реакции при соприкосновении веществ. Конечно, в «химической» области «действий» есть особенности не сводящиеся к молекулам, например, фотохимические реакции, где к объектам необходимо добавить фотоны. Самые простые процессы выбраны для рассмотрения намеренно.

Математические процессы

Следующей областью выберем «действия» из известных нам абстрактных алгоритмов. Самые яркие их представители — математические процессы. В этой области есть действительно «сложные случаи», но для этой статьи достаточно хорошо знакомых примеров. Рассмотрим в качестве «действия» достаточно элементарную операцию — сложение. А примером этого «действия» выберем сложение математиком двух целых чисел.

В ситуации с математиком можно выделить много объектов, но с точки зрения «действия» («сложение математиком двух целых чисел»), объекта всего три: это объект «математик», объект «первое число» и объект «второе число». В отличие от всех рассмотренных ранее объектов числа являются обозначениями, то есть виртуальными объектами. И их преобразование в алгоритме более сложно устроено нежели изменение расстояния и параметров движения объектов, как это было для «химических» действий. Подробности такого преобразования — это тема отдельной увлекательной статьи. А в рамках текущей рассмотрим древнего математика, который складывает числа, используя кучки камешков (рим. ‘calculi’), и более «современного» математика, использующего абак. Абстракции таких способов вычисления суммы не так далеко отошли от физических и химических процессов, поэтому структура процессов их «действий» полностью описывается изменениями расстояний и связей.

Интересно, что на примере древнего математика становится понятен смысл слова «сложить», которое отсылает нас к действию «класть» и к фразе «положить вместе».

Сложение и древний математик

Для математика, оперирующего камешками, сумма это «действие» со следующими характеристиками.

Исходные объекты:

• это сам «математик» (он взаимодействует со слагаемыми);
• лежащая отдельно кучка №1, содержащая и связывающая вместе камешки (подобно химическим связям), и обозначающая первое слагаемое;
• лежащая отдельно кучка камешков №2, обозначающая второе слагаемое.

Процессы:

• «математик» подходит к кучкам (физически изменяет расстояние между кучками и собой) и начинает с ними взаимодействие;
• «математик» объединяет две кучки (физически изменяет расстояние между двумя кучками или переносит все камешки одной кучки в другую, возможно, используя «действие» «Перенос по-одному» камешку)

Результирующие объекты:

• сформированная кучка камешков, обозначающая результат (сумму);
• «математик», отошедший от кучки результата и переставший на неё воздействовать.

Сложение и математик-абакист

У математика с абаком ситуация сложнее. Кучки разделены по значению на разрядные борозды.

Можно рассмотреть самый простой абак с двумя разрядами-бороздами. Пусть он будет десятичный. Тогда один камешек на борозде десятков соответствует десяти камешкам на борозде единиц. И 10 — это максимальное количество камешков на борозде единиц. По сравнению с действием первого математика меняется представление слагаемых. И в арсенале математика уже необходимы нескольких готовых «действий».

Действия:

• «Перенос по-одному» из борозды в борозду одинакового уровня (действие, позаимствованное у первого математика);
• «Перенос в десятки», которое необходимо выполнять, если борозда единиц полностью заполняется, тогда из неё убираются все камешки кроме одного, который переносится в борозду десятков.

Исходные объекты:

• это сам «математик» (он взаимодействует со слагаемыми);
• группа камешков №1, лежащих и удерживаемых двумя бороздами (единиц и десятков), и обозначающих первое слагаемое;
• группа камешков №2, лежащих и удерживаемых двумя бороздами (единиц и десятков), и обозначающих второе слагаемое;

Процессы:

• «математик» подходит к группам борозд (физически изменяет расстояние между ними и собой) и начинает с ними взаимодействие;
• «математик» объединяет камешки из двух борозд единиц (физически изменяет расстояние между камешками, разрушает связи со старой бороздой и создает связи с новой) с использованием действий «Перенос по-одному» и «Перенос в десятки»;
• «математик» объединяет камешки из двух борозд десятков с использованием действия «Перенос по-одному»

Результирующие объекты:

• сформированная группа камешков в двух бороздах (единиц и десятков), обозначающая результат (сумму);
• «математик», отошедший от группы камешков результата и переставший на них воздействовать.

Локальность в этих математических «действиях» описывается отсутствием взаимодействия двух слагаемых, находящихся далеко от математика, и запуском процессов сложения когда все три объекта сложения «близко». Повторяемое изменение в математическом «действии» выражается в изменении связей между камнями и удерживающими их локациями (кучками, бороздами).

Сложение и машина Тьюринга

Можно пойти чуть дальше и заменить математика в таких «действиях» на «управляющее устройство» машины Тьюринга. Тогда «ячейки ленты» машины Тьюринга будут содержать слагаемые.

При этом остаётся и признак локальности как возможность взаимодействия управляющего устройства только с текущей ячейкой ленты, и признак изменения параметров объектов, который можно описать как изменение состояния ячеек.

Подробное описание исходных и результирующих состояний объектов, а так же «действий» производящих эти изменения для сложения, исполняемого машиной Тьюринга, оставим за рамками этой статьи. Но упомянем, что перейдя к машине мы снижаем требования к исполнителю «действия», что является главным способом для создания формальных методов работы с алгоритмом. Можно поставить себе целью упрощение каждой составляющей алгоритма до состояния, когда её выполнение можно будет поручить компьютеру. Тогда в определении алгоритма не останется тёмных мест, и многочисленные вопросы, перечисленные в начале, найдут свои ответы. Пока формализован только исполнитель. Скажем спасибо за это Тьюрингу и вспомним про «действие», формализация которого уже на пороге.

Выводы

Соберём всё, что мы отметили рассматривая разные примеры «действия»:

• «действие» можно использовать для создания алгоритма;
• «действие» может быть элементарным;
• «действие» может быть реализовано алгоритмом;
• в «действии» обязательно участвует некоторый объект или группа объектов;
• для группы объектов «действие» происходит только тогда, когда эти объекты «достаточно близко»;
• в действии изменяются связи и параметры объектов (включая параметры их движения);
• «действие» всегда и обязательно должно быть повторимо.

Признак Повторимости помогает нам в создании наших алгоритмов. С его использованием мы из всех процессов выделяем те, что являются «действием» и на их основе создаём новые алгоритмы. Более того этот признак достаточно прост и на основе его формализации можно снизить требования к системе обнаруживающей и создающей «действия» и поручить это нашему компьютеру.

Следующая статья серии (Часть 2) будет посвящена рассмотрению способов, с использованием которых «действия» могут быть сгруппированы в алгоритм. Этих способов достаточно много и есть предпосылки, что их описание не получится уместить в одну статью. Напишем — увидим.

Спасибо Вам за внимание.

Отзывы

Буду очень благодарен за отзывы и предложения, так как они помогают мне скорректировать направление развития работы в области.

Отдельное волнение у меня есть по стилю и форматированию, используемым в статье (кавычки, абзацы, курсив). Напишите, пожалуйста, если у Вас есть замечания к ним. Можно личным сообщением.

Ссылки

• Главная страница и теория работы (GitLab GPL): Проект «Общая теория алгоритмов»
• Вводная статья работы «Разрабатываем теорию алгоритмов как проект с открытым исходным кодом». Пожалуйста, не судите строго эту наивную публикацию «сверх-идеи» устаревшей версии 2019 года.
• Статьи серии «Что такое алгоритм?!»
  • №1 «Действие» (текущая)
  • №2 «Жизнь»
  • №3 «Синтез алгоритма запоминанием»
  • №3.1 «Эволюция памяти»
  • №3.14 «Обучение»
  • №5 «Эволюция поведения»
  • №4 «Математика»
  • №4.0 «Физика»
  • №3.25 «Язык»
  • №5.0 «Философия»
  • №5.00 «Искусственный интеллект»
• Статьи в хабе «Программирование»:
  • Детская сказка программисту на ночь
  • Эволюция программного проекта и ООП
  • Как не понимать принципы развития архитектуры SOLID
• Все рисунки к статье (кроме заглавного) сформированы сообществом Wikipedia. Лицензия (Creative Commons Attribution-Share Alike 4.0 International)

Материал из MachineLearning.

Перейти к: навигация, поиск

Алгори́тм — это точный набор инструкций, описывающих порядок действий некоторого исполнителя для достижения результата, решения некоторой задачи за конечное время.

Общие определения

Единого «истинного» определения понятия «алгоритм» нет.
Наиболее известные варианты определения опираются на интуитивное понятие «задачи»:

• Алгоритм — это конечный набор правил, который определяет последовательность операций для решения конкретного множества задач и обладает пятью важными чертами: конечность, определённость, ввод, вывод, эффективность (Д. Э. Кнут).
• Алгоритм — это всякая система вычислений, выполняемых по строго определённым правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи (А. Н. Колмогоров).
• Алгоритм — это последовательность действий, либо приводящяя к решению задачи, либо поясняющая, почему это решение получить нельзя.

Формальные признаки алгоритмов

• Детерминированность: в каждый момент времени следующий шаг работы однозначно определяется состоянием исполнителя. Алгоритм выдаёт один и тот же результат (ответ) для одних и тех же исходных данных.
• Понятность: алгоритм должен включать только команды из заранее оговоренной системы команд исполнителя.
• Завершаемость (конечность): при корректно заданных исходных данных алгоритм должен завершать работу и выдавать результат за конечное число шагов.
• Массовость: алгоритм должен быть применим к разным наборам исходных данных.

Алгоритмы анализа данных

В анализе данных под алгоритмом понимается функция,
преобразующая входные данные в выходные данные,
эффективно вычислимая на компьютере за конечное время,
точнее, за приемлемо малое для данной задачи время.

В машинном обучении понятие алгоритм может употреблять в трёх смыслах.

Литература

1. Рудаков, К. В. Алгебраическая теория универсальных и локальных ограничений для алгоритмов распознавания: Дис. док. физ.-мат. наук: 05-13-17. — Вычислительный центр АН СССР, 1992. — 274 с.  (подробнее)

Ссылки

• Алгоритм — Википедия (русский).
• Algorithm — Wikipedia (english).

Человеку в жизни
приходится решать множество разнообразных
задач. Простые задачи имеют простое
решение, а для решения сложных задач
используются различные приемы, способы,
системы и т.п. Понятие «алгоритм»
связано, как правило, с решением сложных
задач, требующих привлечения вычислительной
техники. Вместе с тем, это понятие можно
использовать и при описании простых
операций и решений.

Примеры простых
решений, в которых используются
алгоритмические подходы:

• рецепты
  кулинарной книги;

• порядок
  автоматической стирки;

• кипячение
  воды в чайнике.

Понятие «алгоритм»
связано, как правило, с решением сложных
задач, требующих привлечения вычислительной
техники.

Алгоритм
– набор инструкций, описывающих порядок
действий исполнителя для достижения
результата решения задачи за конечное
время⁸.

Алгоритм
– это конечный набор правил, позволяющих
чисто механически решать любую конкретную
задачу из некоторого класса однотипных
задач⁹.

Различают процессы
создания и реализации алгоритмов.

Создание
алгоритма
– творческий
процесс, выполняемый специалистом в
области разработки алгоритмов.

Реализация
– процесс
выполнения предписанных команд формальным
исполнителем, к которым, в первую очередь,
относятся различные автоматические
устройства, в том числе, вычислительная
техника.

Формальный
исполнитель не вникает в смысл того,
что он делает, но получает при этом
необходимый результат. Строгое выполнение
последовательности операций с отвлечением
исполнителя от содержания поставленной
задачи выражается в особенности, которая
называется формальностью
алгоритма.

Алгоритм –
искусственная конструкция,
которая строится по определенным
правилам и характеризуется конкретными
свойствами.

1. Дискретность.
   Одно из свойств алгоритма, которое
   выражается в разбиении описываемого
   процесса на последовательность отдельных
   шагов или команд. Совокупность отдельных
   шагов образует дискретную
   структуру алгоритма.

2. Понятность.
   Для создания алгоритма могут быть
   использованы только те команды, которые
   исполнитель понимает и может выполнить.
   Другими словами, алгоритм должен
   состоять из команд, которые имеются в
   системе
   команд исполнителя.

3. Определённость
   или
   детерминированность.
   При разработке
   алгоритма не могут быть использованы
   команды, смысл которых воспринимается
   исполнителем неоднозначно. Иначе
   говоря, алгоритм не должен оставлять
   места для произвола исполнителя.

4. Результативность.
   Процесс, описываемый алгоритмом, должен
   прекратиться за конечное число шагов
   с получением определённого результата.

5. Массовость.
   Чаще всего алгоритмы обеспечивают
   решение не одной конкретной задачи, а
   некоторого класса задач данного типа.
   Это свойство позволяет выделять область
   применимости алгоритма.

Из перечисленных
свойств вытекают
правила построения алгоритма, которые
выражаются в следующем.

1. Алгоритм приступает
   к работе с набором данных, которые
   называются входными,
   в результате
   работы выдает данные, которые называются
   выходными.
   Таким
   образом,
   алгоритм
   преобразует
   входные данные в выходные.

Это правило
позволяет сразу отделить алгоритмы от
«методов» и «способов». Пока
мы не имеем формализованных входных
данных, мы не можем построить алгоритм.

1. Для работы
   алгоритма требуется дискретная память,
   в ячейках
   которой размещаются входные данные, а
   также промежуточные и выходные данные,
   которые являются результатом работы
   алгоритма.

2. Алгоритм
   строится из отдельных шагов, действий,
   операций или команд, при
   этом множество шагов алгоритма всегда
   конечно.

3. После каждого
   шага необходимо
   указывать, какой шаг в алгоритме
   выполняется следующим, либо
   давать команду на остановку.

4. Алгоритм должен
   завершать работу после конечного числа
   шагов.
   При этом
   необходимо указывать,
   что считать результатом работы
   алгоритма.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Алгоритм — это четкая последовательность действий, выполнение которой дает какой-то заранее известный результат. Проще говоря, это набор инструкций для конкретной задачи. Известнее всего этот термин в информатике и компьютерных науках, где под ним понимают инструкции для решения задачи эффективным способом.

Сейчас под этим словом понимают любые последовательности действий, которые можно четко описать и разделить на простые шаги и которые приводят к достижению какой-то цели. Например, пойти на кухню, налить воду и положить в нее пакетик чая — это алгоритм для выполнения задачи «Заварить чай».

Алгоритмы в информатике — инструкции для компьютеров, набор шагов, который описывается программным кодом. Существуют конкретные алгоритмы для тех или иных действий, причем некоторые из них довольно сложные. Одна из целей использования алгоритмов — делать код эффективнее и оптимизировать его.

Кто пользуется алгоритмами

В общем смысле — абсолютно все живые и некоторые неживые существа, потому что любую последовательность действий, ведущую к цели, можно считать алгоритмом. Поиск еды животным — алгоритм, движения робота тоже описываются алгоритмом.

В узком смысле, в котором понятие используется в компьютерных науках, алгоритмами пользуются разработчики, некоторые инженеры и аналитики, а также специалисты по машинному обучению, тестировщики и многие другие. Это одно из ключевых понятий в IT.

Для чего нужны алгоритмы

Алгоритмы в информатике нужны для эффективного решения различных задач, в том числе тех, выполнение которых «в лоб» имеет высокую сложность или вовсе невозможно. На практике существуют алгоритмы практически для чего угодно: сортировки, прохождения по структурам данных, поиска элементов, фильтрации информации, математических операций и так далее.

Например, отсортировать массив можно в ходе полного перебора — это самое очевидное решение. А можно воспользоваться алгоритмом быстрой сортировки: он сложнее и не так очевиден, зато намного быстрее работает и не так сильно нагружает мощности компьютера. Строго говоря, полный перебор — это тоже алгоритм, но очень простой.

Существуют алгоритмически неразрешимые задачи, для решения которых нет и не может существовать алгоритма. Но большинство задач в IT разрешимы алгоритмически, и алгоритмы активно используются в работе с ними.

Алгоритмы применяются во всех направлениях IT и во многих других отраслях. Инструкции для автоматизированного станка или линии производства — алгоритмы, рецепт блюда — тоже.

Свойства алгоритмов

Дискретность. Алгоритм — не единая неделимая структура, он состоит из отдельных маленьких шагов, или действий. Эти действия идут в определенном порядке, одно начинается после завершения другого.

Результативность. Выполнение алгоритма должно привести к какому-либо результату и не оставлять неопределенности. Результат может в том числе оказаться неудачным — например, алгоритм может сообщить, что решения нет, — но он должен быть.

Детерминированность. На каждом шаге не должно возникать разночтений и разногласий, инструкции должны быть четко определены.

Массовость. Алгоритм обычно можно экстраполировать на похожие задачи с другими исходными данными — достаточно поменять изначальные условия. Например, стандартный алгоритм по решению квадратного уравнения останется неизменным вне зависимости от того, какие числа будут использоваться в этом уравнении.

Понятность. Алгоритм должен включать только действия, известные и понятные исполнителю.

Конечность. Алгоритмы конечны, они должны завершаться и выдавать результат, в некоторых определениях — за заранее известное число шагов.

Какими бывают алгоритмы

Несмотря на слово «последовательность», алгоритм не всегда описывает действия в жестко заданном порядке. Особенно это актуально сейчас, с распространением асинхронности в программировании. В алгоритмах есть место для условий, циклов и других нелинейных конструкций.

Линейные. Это самый простой тип алгоритма: действия идут друг за другом, каждое начинается после того, как закончится предыдущее. Они не переставляются местами, не повторяются, выполняются при любых условиях.

Ветвящиеся. В этом типе алгоритма появляется ветвление: какие-то действия выполняются, только если верны некоторые условия. Например, если число меньше нуля, то его нужно удалить из структуры данных. Можно добавлять и вторую ветку: что делать, если условие неверно — например, число больше нуля или равно ему. Условий может быть несколько, они могут комбинироваться друг с другом.

Циклические. Такие алгоритмы выполняются в цикле. Когда какой-то блок действий заканчивается, эти действия начинаются снова и повторяются некоторое количество раз. Цикл может включать в себя одно действие или последовательность, а количество повторений может быть фиксированным или зависеть от условия: например, повторять этот блок кода, пока в структуре данных не останется пустых ячеек. В некоторых случаях цикл может быть бесконечным.

Рекурсивные. Рекурсия — это явление, когда какой-то алгоритм вызывает сам себя, но с другими входными данными. Это не цикл: данные другие, но «экземпляров» работающих программ несколько, а не одна. Известный пример рекурсивного алгоритма — расчет чисел Фибоначчи.

Рекурсия позволяет изящно решать некоторые задачи, но с ней надо быть осторожнее: такие алгоритмы могут сильно нагружать ресурсы системы и работать медленнее других.

Вероятностные. Такие алгоритмы упоминаются реже, но это довольно интересный тип: работа алгоритма зависит не только от входных данных, но и от случайных величин. К ним, например, относятся известные алгоритмы Лас-Вегас и Монте-Карло.

Основные и вспомогательные. Это еще один вид классификации. Основной алгоритм решает непосредственную задачу, вспомогательный решает подзадачу и может использоваться внутри основного — для этого там просто указываются его название и входные данные. Пример вспомогательного алгоритма — любая программная функция.

Графическое изображение алгоритмов

Алгоритмы могут записывать текстом, кодом, псевдокодом или графически — в виде блок-схем. Это специальные схемы, состоящие из геометрических фигур, которые описывают те или иные действия. Например, начальная и конечная точка на схеме — соответственно, начало и конец алгоритма, параллелограмм — ввод или вывод данных, ромб — условие. Простые действия обозначаются прямоугольниками, а соединяются фигуры с помощью стрелок — они показывают последовательности и циклы.

В схемах подписаны конкретные действия, условия, количество повторений циклов и другие детали. Это позволяет нагляднее воспринимать алгоритмы.

Сложность алгоритма

Понятие «сложность» — одно из ключевых в изучении алгоритмов. Оно означает не то, насколько трудно понять тот или иной метод, а ресурсы, затраченные на вычисление. Если сложность высокая, алгоритм будет выполняться медленнее и, возможно, тратить больше аппаратных ресурсов; такого желательно избегать.

Сложность обычно описывают большой буквой O. После нее в скобках указывается значение, от которого зависит время выполнения. Это обозначение из математики, которое описывает поведение разных функций.

Какой бывает сложность. Полностью разбирать математическую O-нотацию, как ее называют, мы не будем — просто перечислим основные обозначения сложности в теории алгоритмов.

•  O(1) означает, что алгоритм выполняется за фиксированное константное время. Это самые эффективные алгоритмы.
•  O(n) — это сложность линейных алгоритмов. n здесь и дальше обозначает размер входных данных: чем больше n, тем дольше выполняется алгоритм.
•  O(n²) тоже означает, что чем больше n, тем выше сложность. Но зависимость тут не линейная, а квадратичная, то есть скорость возрастает намного быстрее. Это неэффективные алгоритмы, например с вложенными циклами.
•  O(log n) — более эффективный алгоритм. Скорость его выполнения рассчитывается логарифмически, то есть зависит от логарифма n.
•  O(√n) — алгоритм, скорость которого зависит от квадратного корня из n. Он менее эффективен, чем логарифмический, но эффективнее линейного.

Существуют также O(n³), O(nn) и другие малоэффективные алгоритмы с высокими степенями. Их сложность растет очень быстро, и их лучше не использовать.

Графическое описание сложности. Лучше разобраться в сложности в O-нотации поможет график. Он показывает, как изменяется время выполнения алгоритма в зависимости от размера входных данных. Чем более пологую линию дает график, тем эффективнее алгоритм.

O-нотацию используют, чтобы оценить, эффективно ли использовать ту или иную последовательность действий. Если данные большие или их много, стараются искать более эффективные алгоритмы, чтобы ускорить работу программы.

Использование алгоритмов в IT

Мы приведем несколько примеров использования разных алгоритмов в отраслях программирования. На самом деле их намного больше — мы взяли только часть, чтобы помочь вам понять практическую значимость алгоритмов.

Разработка ПО и сайтов. Алгоритмы используются для парсинга, то есть «разбора» структур с данными, таких как JSON. Парсинг — одна из базовых задач, например в вебе. Также алгоритмы нужны при отрисовке динамических структур, выводе оповещений, настройке поведения приложения и многом другом.

Работа с данными. Очень активно алгоритмы применяются при работе с базами данных, файлами, где хранится информация, структурами вроде массивов или списков. Данных может быть очень много, и выбор правильного алгоритма позволяет ускорить работу с ними. Алгоритмы решают задачи сортировки, изменения и удаления нужных элементов, добавления новых данных. С их помощью наполняют и проходят по таким структурам, как деревья и графы. 

Отдельное значение алгоритмы имеют в Big Data и анализе данных: там они позволяют обработать огромное количество информации, в том числе сырой, и не потратить на это слишком много ресурсов.

Поисковые задачи. Алгоритмы поиска — отдельная сложная отрасль. Их выделяют в отдельную группу, в которой сейчас десятки разных алгоритмов. Поиск важен в науке о данных, в методах искусственного интеллекта, в аналитике и многом другом. Самый очевидный пример — поисковые системы вроде Google или Яндекса. Кстати, подробности об используемых алгоритмах поисковики обычно держат в секрете.

Машинное обучение. В машинном обучении и искусственном интеллекте подход к алгоритмам немного другой. Если обычная программа действует по заданному порядку действий, то «умная машина» — нейросеть или обученная модель — формирует алгоритм для себя сама в ходе обучения. Разработчик же описывает модель и обучает ее: задает ей начальные данные и показывает примеры того, как должен выглядеть конечный результат. В ходе обучения модель сама продумывает для себя алгоритм достижения этого результата.

Такие ИИ-алгоритмы могут быть еще мощнее обычных и используются для решения задач, которые разработчик не в силах разбить на простые действия сознательно. Например, для распознавания предметов нужно задействовать огромное количество процессов в нервной системе: человек просто физически не способен описать их все, чтобы повторить программно.

В ходе создания и обучения модели разработчик тоже может задействовать алгоритмы. Например, алгоритм распространения ошибки позволяет обучать нейросети.