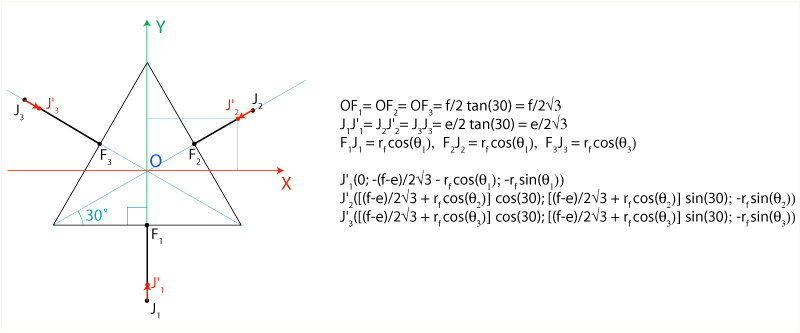Кинематика дельта-робота
Время на прочтение
8 мин
Количество просмотров 46K
В далёком 2009 году я загорелся идеей постройки собственного промышленного робота, который мог бы делать что-то полезное (а именно — сортировать мелкие детали на конвейере). Сразу скажу, что робота я построил (результат вы видите на заглавном фото), а заодно, в качестве побочного продукта, написал небольшую статью о кинематике дельта-роботов на форуме TrossenRobotics — американского продавца наборов из деталей для роботов. Они как раз проводили в то время какой-то конкурс для авторов. Конкурс я, разумеется, не выиграл, но статья на английском осталась. Несколько раз я порывался перевести её на родной язык, однако завершить начатое удалось только сейчас.
Если вы хотите построить свою модель дельта-робота, или просто разобраться, как можно вывести кинематические формулы для этого типа роботов (не выходя при этом за рамки школьной программы по алгебре и геометрии) — добро пожаловать под кат. Для тех, кто не очень любит теорию, в конце статьи приведены примеры готового кода на языке C.
Что такое дельта-робот
Дельта-робота (wiki) придумал в начале 1980-х швейцарский учёный Реймонд Клавель, ниже приведена иллюстрация из оригинального патента US4976582 на «Устройство для перемещения и позиционирования элемента в пространстве»:
Робот состоит из двух платформ: неподвижно закреплённого верхнего основания (1) и небольшой подвижной платформы (8), соединённых тремя рычагами. Каждый рычаг состоит из двух частей: верхнее плечо (4) жёстко соединено с двигателем (3), расположенным на верхнем основании, а нижнее представляет собой параллелограмм (5), в углах которого установлены т.н. универсальные шарниры (6, 7) (wiki), которые позволяют углам изменяться. Каждый параллелограмм соединён с верхним рычагом шарниром (16) таким образом, чтобы его верхняя сторона всегда оставалась перпендикулярной своему рычагу и параллельной плоскости верхнего основания. Благодаря этому подвижная платформа робота, прикреплённая к нижним сторонам параллелограммов также будет всегда параллельной верхнему основанию. Управлять положением платформы мы сможем, изменяя угол поворота верхних рычагов относительно основания робота при помощи двигателей.
В центре нижней платформы (8) крепится т.н. рабочий орган (в английском языке употребляют термин end effector) робота (9). Это может быть манипулятор, захватывающее устройство или, например, экструдер в случае 3D принтера. Дополнительно может использоваться ещё один двигатель (11), который обеспечивает вращение рабочего органа через штангу (14).
Главным преимуществом дельта-роботов является скорость: тяжёлые двигатели размещены на неподвижном основании, движутся только рычаги и нижняя платформа, которые стараются изготавливать из лёгких композитных материалов, уменьшая тем самым их инерцию. Вот, к примеру, статья на Geektimes с парой очень эффектных видеороликов.
Формулировка задачи
Чтобы построить своего собственного дельта-робота, необходимо научиться решать две задачи. В первой ситуации нам известна позиция, в которую мы хотим переместить манипулятор нашего робота (например, мы хотим схватить печенье, которое находится на конвейере в точке с координатами (x, y, z). Для этого нам требуется определить величины углов, на которые мы должны повернуть двигатели, связанные с рычагами робота, чтобы установить его в правильное положение для захвата. Процедура определения этих углов называется обратной (в некоторых русскоязычных источниках употребляется слово «инверсной») кинематической задачей.
Во второй ситуации нам известны углы, на которые повёрнуты управляющие моторы робота (если мы используем сервомоторы, то углы легко можно узнать, считав показания с датчиков углов поворота), и мы хотим найти положение платформы робота в пространстве (например, чтобы скорректировать его позицию). Это — прямая кинематическая задача.
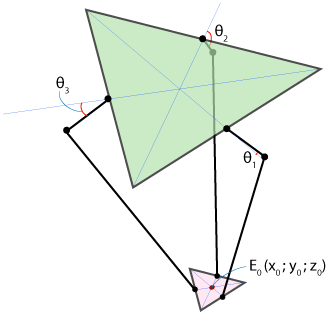
Формализуем обе задачи. И неподвижное основание робота, и его движущуюся платформу можно представить в виде равносторонних треугольников: на схеме ниже они закрашены зелёным и розовым цветами соответственно. Углы поворота рычагов робота относительно плоскости основания (они же — углы поворота моторов) обозначены как Ѳ1, Ѳ2 и Ѳ3, а координаты точки Е0, расположенной в центре подвижной платформы и в которой в реальной жизни будет закреплён манипулятор нашего робота — как (x0, y0, z0).
Получается, что мы должны придумать две функции:
- finverse(x0, y0, z0) → (Ѳ1, Ѳ2, Ѳ3) для решения обратной кинематической задачи и
- fforward(Ѳ1, Ѳ2, Ѳ3) → (x0, y0, z0) для решения прямой кинематической задачи.
Обратная кинематика
Зададим несколько ключевых параметров, которые определяются геометрическими размерами нашего робота:
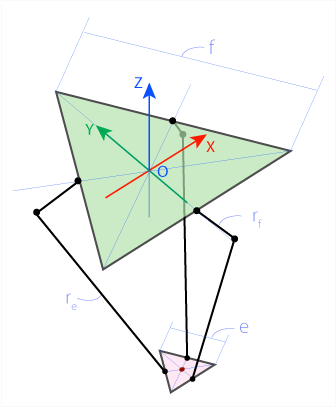
Обозначим длину стороны верхнего основания f, сторону нижней платформы e, длину верхнего плеча рычага rf и длину нижнего плеча (длинной стороны параллелограмма) re. Для вычислений выберем систему координат с точкой отсчёта, совпадающей с геометрическим центром верхнего треугольника. Ось Z направим вверх, таким образом, z-координата подвижной платформы всегда будет отрицательной.
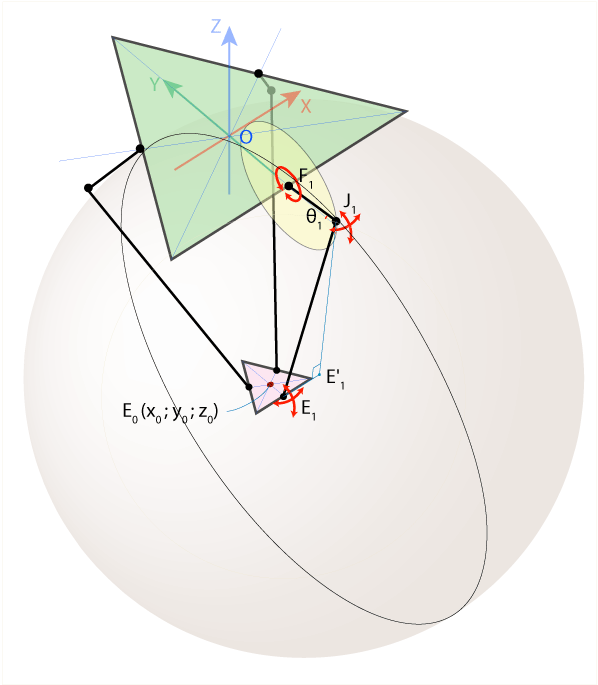
Конструкция робота подразумевает, что рычаг F1J1 (см. рисунок ниже) может вращаться лишь в плоскости YZ, описывая при этом окружность радиусом rf с центром в точке F1 (именно в этом месте он прикреплён к двигателю). В отличие от F1, в узлах J1 и E1 используются универсальные шарниры, благодаря которым плечо E1J1 может свободно вращаться относительно E1, описывая сферу радиусом re с центром в точке E1.
Пересечением этой сферы и плоскости YZ является окружность с центром в точке E’1 радиусом E’1J1, где точка E’1 находится как проекция точки E1 на плоскость YZ. Тогда точка J1 будет находиться на пересечении двух окружностей с центрами в точках E’1 и F1, причём радиусы этих окружностей мы можем определить. Тут есть небольшая тонкость: окружности пересекаются в двух точках, но нас интересует только одна из них — с меньшим значением координаты y, поскольку мы хотим, чтобы рычаги робота всегда торчали «локтями» наружу. Определив таким образом координаты точки J1, мы легко сможем найти угол интересующий нас угол Ѳ1.
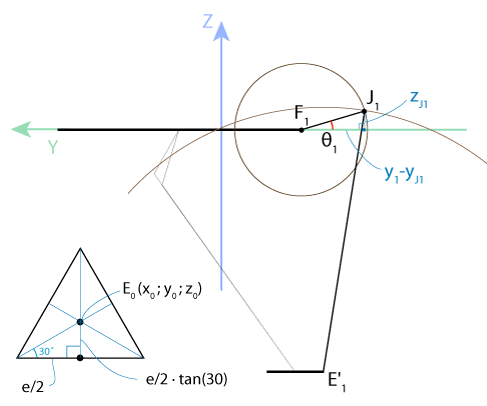
Для удобства восприятия ниже показана проекция нашей трёхмерной картинки на плоскость YZ:
Нижняя платформа является равносторонним треугольником, центром которого является точка E0(x0, y0, z0). Значит, расстояние
что даёт нам следующие координаты точки E1 и её проекции E’1 на плоскость YZ:
Расстояние E1E’1=x0, тогда, согласно теореме Пифагора,
Поскольку верхняя платформа также является равносторонним треугольником, то координаты у точки F1 будут
Чтобы найти координаты точки J1, являющейся пересечением двух окружностей, надо решить систему уравнений:
Координаты центров окружностей нам известны, если их подставить, получится следующее выражение:
Если раскрыть скобки и вычесть одно уравнение из другого, можно линейным образом выразить z-координату точки J1 через y-координату, после чего, подставив её во второе уравнение, получим обычное квадратное уравнение относительно y, из двух решений которого выберем наименьшее (об этом мы говорили выше). А получив таким образом координаты точки J1, найдём и угол
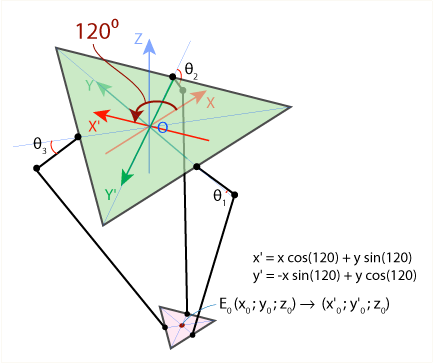
Все выражения получились достаточно простыми благодаря удачному выбору системы координат: плечо рычага F1J1 всегда движется в плоскости YZ, поэтому мы можем просто не учитывать координату x. Чтобы сохранить это преимущество при нахождении двух оставшихся углов Ѳ2 и Ѳ3, воспользуемся симметрией конструкции дельта-робота. Сначала повернём нашу систему координат на 120° против часовой стрелки в плоскости XY вокруг оси Z:
Мы получили новую систему координат X’Y’Z’, и в этой новой системе мы можем воспользоваться нашими готовыми формулами для нахождения угла Ѳ2. Единственная тонкость заключается в том, что мы должны предварительно пересчитать координаты точки E0 в новой системе отсчёта. Это легко сделать при помощи известной формулы (преобразования при повороте системы вокруг начала координат), показанной на рисунке выше. Для нахождения угла Ѳ3 необходимо будет также повернуть исходную систему отсчёта, но теперь уже по часовой стрелке. Этот приём очень удобно реализуется в виде программы: достаточно написать функцию для вычисления угла Ѳ в плоскости YZ, а затем вызвать её три раза для каждого из углов и систем отсчёта.
Прямая кинематика
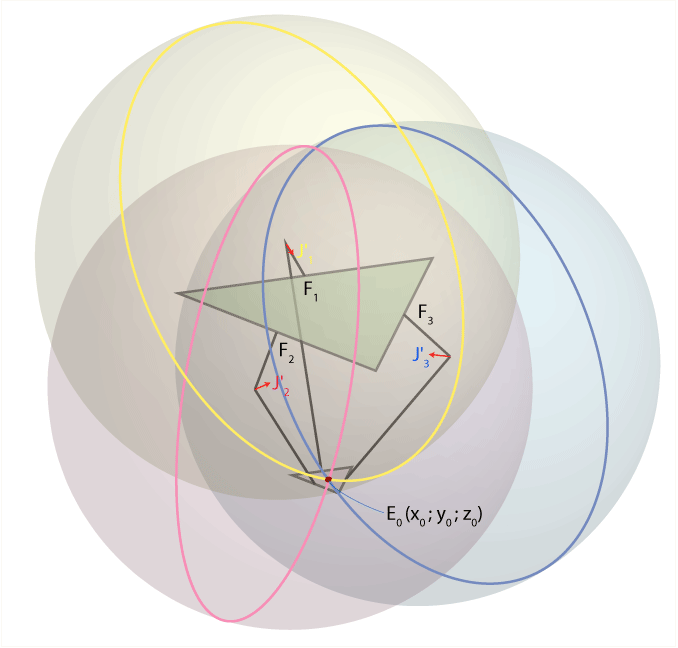
Попробуем решить обратную задачу: теперь нам известны углы Ѳ1, Ѳ2 и Ѳ3, и мы хотим найти координаты (x0, y0, z0) точки E0, расположенной в центре подвижной платформы нашего робота. Зная углы, мы легко можем найти координаты точек J1, J2 и J3 (см. рисунок ниже). Плечи рычагов J1E1, J2E2 и J3E3 могут свободно вращаться вокруг точек J1, J2 и J3 соответственно, образуя в пространстве три сферы с радиусами re.
Воспользуемся хитрым приёмом: сместим центры каждой из этих сфер из точек J1, J2, J3 в плоскости XY в направлении оси Z, используя вектора смещения E1E0, E2E0 и E3E0 соответственно (на рисунке они показаны в виде красных стрелочек). После этого преобразования окажется, что все три сферы пересекаются в точке E0, как показано на рисунке ниже:
Получается, что для определения координат (x0, y0, z0) точки E0 мы должны найти точку пересечения трёх сфер, радиусы и координаты центров которых нам известны. Иными словами, нам надо решить систему из трёх уравнений, описывающих трёхмерные сферы:
где (xi, yi, zi) — координаты центров сфер J’1, J’2 и J’3, которые можно найти следующим образом:
Ниже для сокращения записи я буду использовать в качестве координат точек J’1, J’2 и J’3 обозначения (x1, y1, z1), (x2, y2, z2) и (x3, y3, z3) соответственно. Также хочу обратить внимание, что x1=0 (поскольку точка J’1 находится в плоскости YZ). Получаем следующую систему уравнений:
Введем обозначение
и, вычтя из верхнего уравнения второе и третье, а также из второго третье, получим:
Вычитая из первого уравнения второе (сократив, таким образом, y) и из второго третье (сократив x), сможем выразить x и y через z:
Теперь, подставив x и y, выраженные через z, в уравнение для первой окружности (с центром в точке J’1), получим:
Осталось решить это квадратное уравнение (стандартным образом, через дискриминант), чтобы найти z (мы помним, что надо выбирать наименьший из двух z!), а через него x и y.
Примеры исходного кода
Ниже приведены примеры функций для расчёта кинематики дельта-робота на языке С. Названия переменных соответствуют обозначениям, используемым в статье, углы theta1, theta2 и theta3 указываются в градусах.
// размеры робота
// (обозначения см. на схеме)
const float e = 115.0; // сторона подвижной платформы
const float f = 457.3; // сторона неподвижного основания
const float re = 232.0;
const float rf = 112.0;
// тригонометрические константы
const float sqrt3 = sqrt(3.0);
const float pi = 3.141592653; // PI
const float sin120 = sqrt3/2.0;
const float cos120 = -0.5;
const float tan60 = sqrt3;
const float sin30 = 0.5;
const float tan30 = 1/sqrt3;
// прямая кинематика: (theta1, theta2, theta3) -> (x0, y0, z0)
// возвращаемый статус: 0=OK, -1=несуществующая позиция
int delta_calcForward(float theta1, float theta2, float theta3, float &x0, float &y0, float &z0) {
float t = (f-e)*tan30/2;
float dtr = pi/(float)180.0;
theta1 *= dtr;
theta2 *= dtr;
theta3 *= dtr;
float y1 = -(t + rf*cos(theta1));
float z1 = -rf*sin(theta1);
float y2 = (t + rf*cos(theta2))*sin30;
float x2 = y2*tan60;
float z2 = -rf*sin(theta2);
float y3 = (t + rf*cos(theta3))*sin30;
float x3 = -y3*tan60;
float z3 = -rf*sin(theta3);
float dnm = (y2-y1)*x3-(y3-y1)*x2;
float w1 = y1*y1 + z1*z1;
float w2 = x2*x2 + y2*y2 + z2*z2;
float w3 = x3*x3 + y3*y3 + z3*z3;
// x = (a1*z + b1)/dnm
float a1 = (z2-z1)*(y3-y1)-(z3-z1)*(y2-y1);
float b1 = -((w2-w1)*(y3-y1)-(w3-w1)*(y2-y1))/2.0;
// y = (a2*z + b2)/dnm;
float a2 = -(z2-z1)*x3+(z3-z1)*x2;
float b2 = ((w2-w1)*x3 - (w3-w1)*x2)/2.0;
// a*z^2 + b*z + c = 0
float a = a1*a1 + a2*a2 + dnm*dnm;
float b = 2*(a1*b1 + a2*(b2-y1*dnm) - z1*dnm*dnm);
float c = (b2-y1*dnm)*(b2-y1*dnm) + b1*b1 + dnm*dnm*(z1*z1 - re*re);
// дискриминант
float d = b*b - (float)4.0*a*c;
if (d < 0) return -1; // несуществующая позиция
z0 = -(float)0.5*(b+sqrt(d))/a;
x0 = (a1*z0 + b1)/dnm;
y0 = (a2*z0 + b2)/dnm;
return 0;
}
// обратная кинематика
// вспомогательная функция, расчет угла theta1 (в плоскости YZ)
int delta_calcAngleYZ(float x0, float y0, float z0, float &theta) {
float y1 = -0.5 * 0.57735 * f; // f/2 * tg 30
y0 -= 0.5 * 0.57735 * e; // сдвигаем центр к краю
// z = a + b*y
float a = (x0*x0 + y0*y0 + z0*z0 +rf*rf - re*re - y1*y1)/(2*z0);
float b = (y1-y0)/z0;
// дискриминант
float d = -(a+b*y1)*(a+b*y1)+rf*(b*b*rf+rf);
if (d < 0) return -1; // несуществующая точка
float yj = (y1 - a*b - sqrt(d))/(b*b + 1); // выбираем внешнюю точку
float zj = a + b*yj;
theta = 180.0*atan(-zj/(y1 - yj))/pi + ((yj>y1)?180.0:0.0);
return 0;
}
// обратная кинематика: (x0, y0, z0) -> (theta1, theta2, theta3)
// возвращаемый статус: 0=OK, -1=несуществующая позиция
int delta_calcInverse(float x0, float y0, float z0, float &theta1, float &theta2, float &theta3) {
theta1 = theta2 = theta3 = 0;
int status = delta_calcAngleYZ(x0, y0, z0, theta1);
if (status == 0) status = delta_calcAngleYZ(x0*cos120 + y0*sin120, y0*cos120-x0*sin120, z0, theta2); // rotate coords to +120 deg
if (status == 0) status = delta_calcAngleYZ(x0*cos120 - y0*sin120, y0*cos120+x0*sin120, z0, theta3); // rotate coords to -120 deg
return status;
}
Используемая литература
Все ключевые идеи о кинематике дельта-робота я взял из работы проф. Paul Zsombor-Murray «Descriptive Geometric Kinematic Analysis of Clavel’s «Delta» Robot». Честно признаюсь, что моей математической подготовки не хватило, чтобы понять её до конца, поэтому многое пришлось выводить самому.
Заключение
Спасибо всем, кто прочитал эту статью до конца. Надеюсь, для кого-то она окажется полезной и вдохновит на создание своих вариантов дельта-робота.
Учебный манипулятор с угловой кинематикой
Учебный манипулятор с угловой кинематикой для применения в рамках соревнований в области промышленной автоматизации и «Интернет вещей».
Есть в наличии
Нужна консультация?
Цена действительна только для интернет-магазина и может отличаться от цен в розничных магазинах
Описание
Учебный манипулятор реализован на основе интеллектуальных сервомодулей Dynamixel и специализированной системы управления. Благодаря применению высококачественных сервомодулей Dynamixel, применяемых в профессиональной деятельности в сфере робототехники, учебный манипулятор обладает повышенной точностью и повторяемостью позиционирования исполнительного органа (схвата) по сравнению с какими-либо другими учебными моделями. Наличие встроенной системы управления сервомодулей Dynamixel и множества обратных связей обеспечивает возможность гибкой настройки и управления манипулятором в процессе его работы.
Для управления манипуляционным роботом применяется модульный робототехнический контроллер, что обеспечивает возможность модернизации и расширения функциональных возможностей. Представленные ниже технические особенности позволяют применять данный манипуляционный РТК для разработки макета производственной линии, применяемого в рамках соревнований .
Технические особенности:
- Сбалансированные оси вращения с подшипниковыми узлами.
- Наличие крепежа для модуля технического зрения на схвате манипулятора.
- Манипуляционный РТК выполнен на базе сервомодулей Dynamixel: МХ-64Т – 2 шт, МХ-28Т – 2 шт, АХ-12А – 2 шт (или сервомодули Dynamixel с более лучшими техническими характеристиками).
- Радиус зоны сервиса — не менее 30 см.
- Номинальная грузоподъемность – 250 грамм.
- Грузоподъемность – 450 грамм, в зависимости от ориентации схвата в кратковременном режиме.
- Максимальная грузоподьемность – до 800 грамм в кратковременном режиме.
- Для управления РТК используется программируемый контроллер STEM Board c возможностью встраивания модулей расширения:
— Программируемый контроллер OpenCM – наличие,
— Встраиваемый одноплатный микрокомпьютер – отсутствует (приобретается опционально). - Наличие сетевого адаптера для питания от сети 220В.
- Наличие интерфейсного кабеля для программирования.
- Поставляется в деревянном боксе для хранения и транспортировки.
- Гарантия – 6 месяцев.
Учебный манипулятор обладает встроенным программным обеспечением для коммуникации с облачным сервером РТС ThingWorx, применяемым для разработки приложений с использованием технологий «Интернет вещей». Встроенная система управления учебного манипулятора обеспечивает возможность объединения аналогичных учебных моделей в единую информационную систему для управления группой роботов в рамках решения учебной технологической задачи.
Манипуляторы с угловым типом кинематической схемы могут применяться для свободного перемещения рабочего инструмента в пространстве в рамках сферической рабочей зоны относительно системы координат основания. В большинстве случаев подобные манипуляторы применяются для выполнения задач по перемещению и точному позиционированию объектов, обработки пространственных контуров и поверхностей. Данный тип кинематики является наиболее распространенным в промышленности в области машиностроения и механической обработки, сварочных и покрасочных работ.
Учебный манипулятор представляет собой доступную учебную модель промышленного манипуляционного робота, обеспечивающую возможность на практике изучить большинство аспектов разработки систем управления манипуляционных роботов с угловым типом кинематики, а базовых принципов применения робототехники при автоматизации технологических процессов.
Характеристики
|
Тип |
Наборы |
|
Возрастная группа |
Основная школа (11-15 лет) |
-
Оснащение учебного кабинета
- Интерактивные панели
-
Аксессуары для интерактивных панелей
- Интерактивные комплекты
- Интерактивные доски
- Аксессуары для интерактивных досок
- Интерактивные приставки
- Документ-камеры
- Экраны для проекторов
-
Мультимедийные проекторы
- Аксессуары для проекторов
- Магнитно-маркерные и меловые доски
- Компьютеры
- МФУ, принтеры, сканеры
- Классы виртуальной реальности
- Интерактивные кульманы
-
Интерактивные планшеты
- Интерактивные трибуны
- Интерактивные классы
- Наглядные пособия
- Интерактивные рельсовые системы
- Стенды для школы
- Кабели и переходники
-
3D оборудование
- 3D-принтеры
- 3D-сканеры
- Пластик для 3D-принтеров
- Голографическое оборудование
- Аксессуары для 3D принтеров и сканеров
-
Кабинет иностранных языков
-
Лингафонный кабинет
-
Лингафонный кабинет
-
Кабинет дистанционного обучения
- Системы опроса и тестирования
- Системы видеоконференцсвязи (ВКС)
- Видеостудии
-
Лабораторный кабинет
- Цифровые лаборатории
-
Цифровые микроскопы
- Комплекты лабораторного оборудования
- Оптические микроскопы
- Потолочные системы электроснабжения
- Телескопы
- Электронные информационные таблицы
-
Дошкольное развитие
-
Интерактивные столы
- Набор психолога Пертра
- Интерактивный пол
- Educonsulting
- ЛогоРобот Bee Bot
- Ландшафтные столы
- Интерактивные песочницы
- Ожившие рисунки
- Основы Финансовой грамотности в ДОУ
-
Логопедическое оборудование
- Интерактивные стены
- Напольные конструкторы
- Кабинет психолога
- Методические интерактивные комплексы
- Интерактивные парты
- Мультипликационные студии
-
Тактильные панели
- Детские наборы для исследований
- Развивающие наборы
- Деревянные конструкторы
-
Интерактивные столы
-
Кабинет технологии
- Станки UNIMAT
- Станки Экзамен-Технолаб
-
Станки The First Tool
- Станки TRIOD
- Детские наборы инструментов
- ЧПУ станки
- Комплектующие для ЧПУ станков
-
Кабинет робототехники и программирования
- ROBOTIS
-
LEGO Education
- VEX Robotics
- Экзамен-Технолаб
- MATRIX
- TETRIX
-
Амперка
- Makeblock
- Ubtech
- Dobot
- MatataLab
- Robo WUNDERKIND
- Наборы для сборки квадрокоптеров
- НАУРОБО
- Столы для робототехники
- Releon
- РОББО
- Luxrobo
- Познайкино
- Mojobot
- DJI
- R:ED X
- Mindsensors
- Twin
- HiTechnic
- KUBO
- Океаника
- АЛМА
- BRLab
- Learning Resources
- DFRobot
- DIGIS
- Nexus
- RoboRobo
- Shape Robotics
- Эвольвектор
- Applied Robotics
- CyberToy
- Поля для соревнований
- Botzees
- Tinkamo
- Hiwonder
- Sphero
- Promobot
- АЭРО
- Дополнительное образование
-
Физкультурный зал
- Интерактивный скалодром
- Интерактивная физкультура
- Спортивные игровые комплекты
- Интерактивные тиры
- Спортивные комплексы
-
Digital Signage
- Сенсорные моноблоки
- Гостиничные телевизоры
- Сенсорные мониторы
- Профессиональные панели
- Сенсорные киоски
- Уличные телевизоры
- Коммерческие телевизоры
- Мониторы
- Видеостены
- Информационные киоски
- Коммутационное оборудование
- Светодиодные экраны
- Крепления для видеостен
- Роботы для бизнеса
- Программное обеспечение для профессиональных панелей
-
Cанитарно-гигиеническое оборудование
- Дезинфекторы
- Рециркуляторы
-
Мебель
- Сенсорная комната
- Мебель для образовательных учреждений
-
Доступная среда
- Реабилитационное оборудование
-
Звуковое оборудование
- Кабели
- Полочные акустические системы
- Портативные акустические системы
- Встраиваемые акустические системы
- Активные акустические системы
- Пассивные акустические системы

Введение:
В данном уроке, двигаясь по шагам, мы соберём робот «Манипулятор».
Видео:
Для сборки нам понадобится крепеж:
| Наименование | Количество, шт. | |
|---|---|---|
| 1 | Гайка М3 | 10 |
| 2 | Винт М3х6 | 9 |
| 3 | Винт М3х8 | 10 |
| 4 | Винт М3х10 | 5 |
| 5 | Винт М3х12 | 7 |
| 6 | Винт М3х20 | 4 |
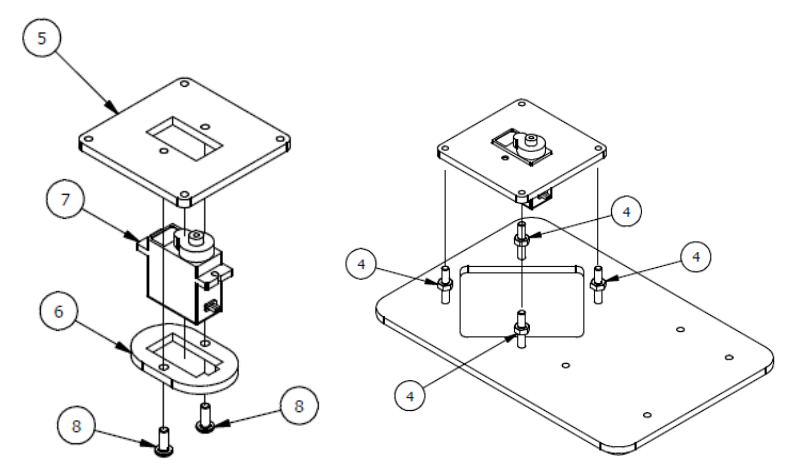
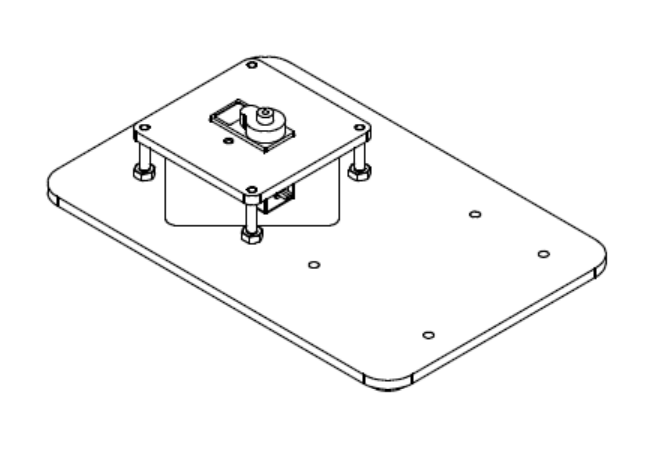
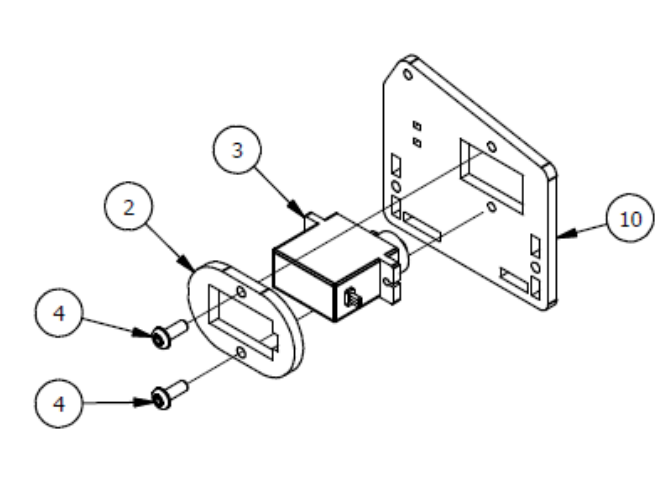
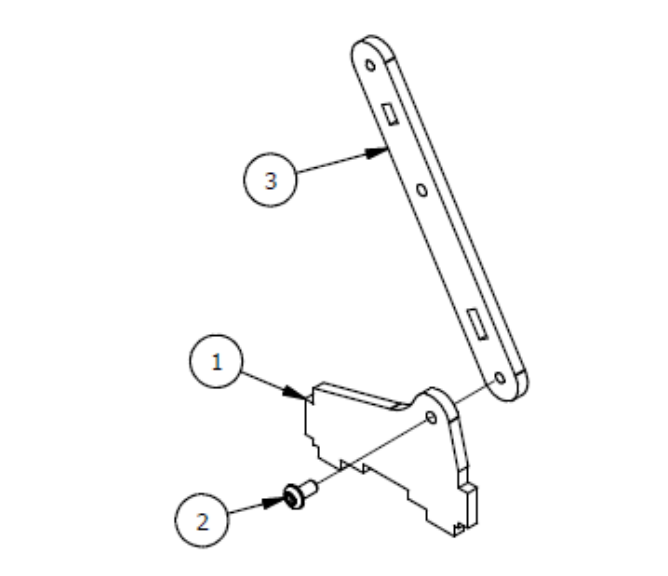
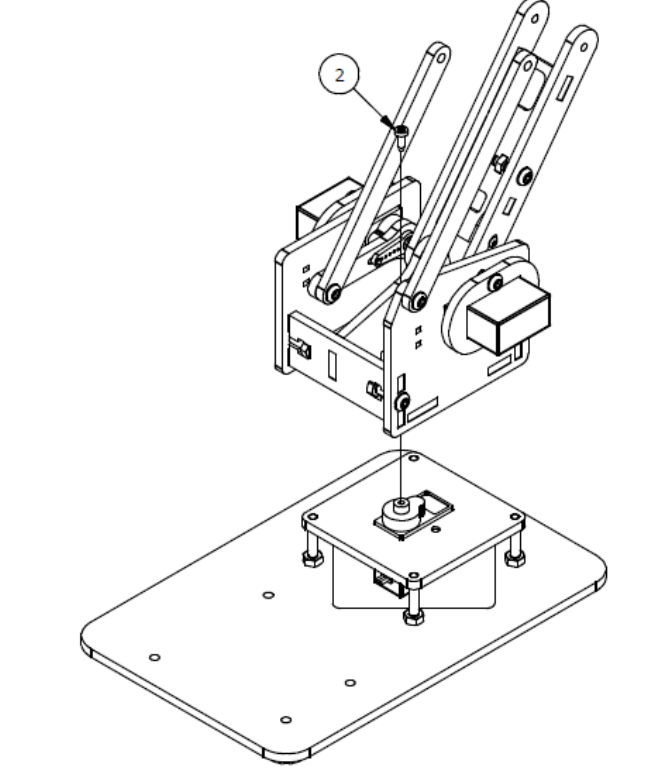
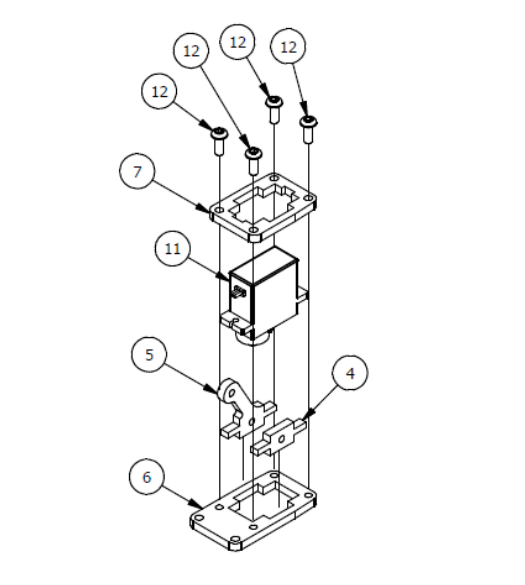
Шаг 1
Список деталей к Шагу 1
Если Вы используете для сборки Микросервопривод MG90S, необходимо отклеить с него наклейки!!! в противном случае он будет очень туго устанавливаться, в результате чего можете поломать крепеж!
| Номер позиции | Количество | Название |
|---|---|---|
| 1 | 1 | Основание |
| 3 | 4 | М3х20мм винт |
| 4 | 4 | М3 гайка |
| 5 | 1 | Опорная пластина |
| 6 | 1 | Крепление |
| 7 | 1 | Сервопривод |
| 8 | 2 | М3×8мм винт |
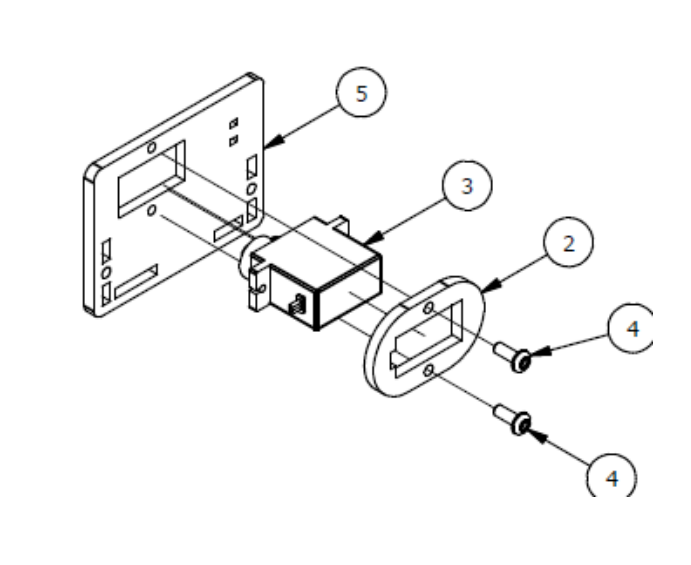
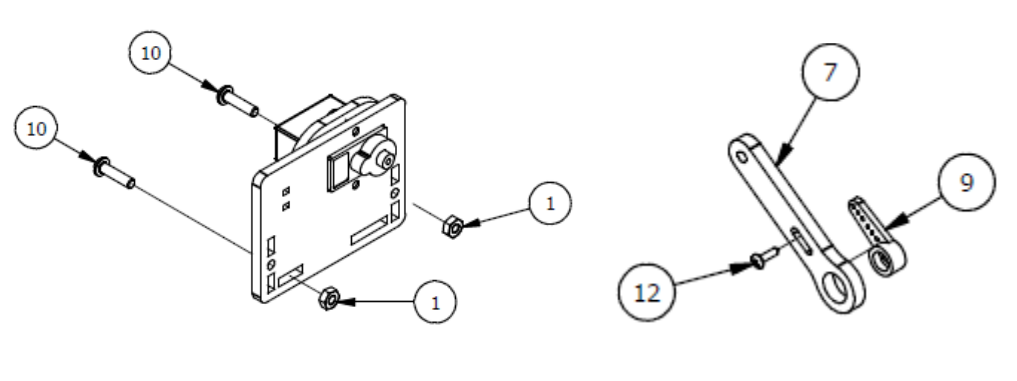
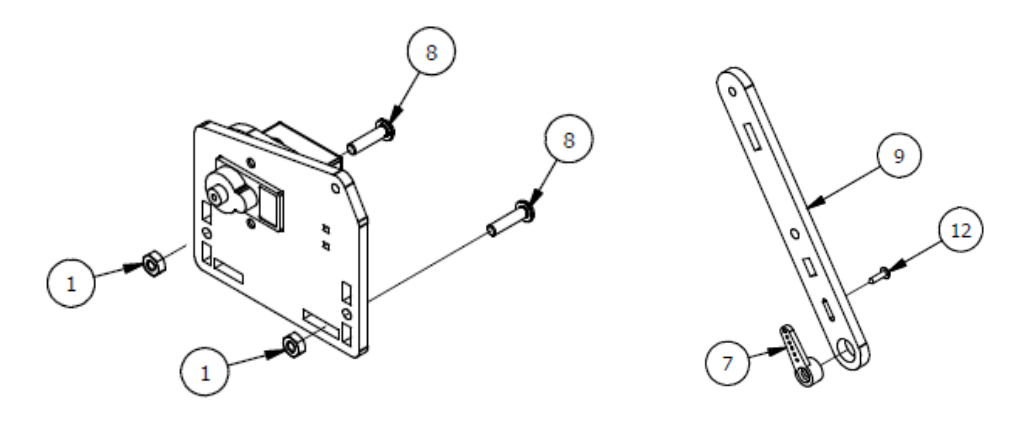
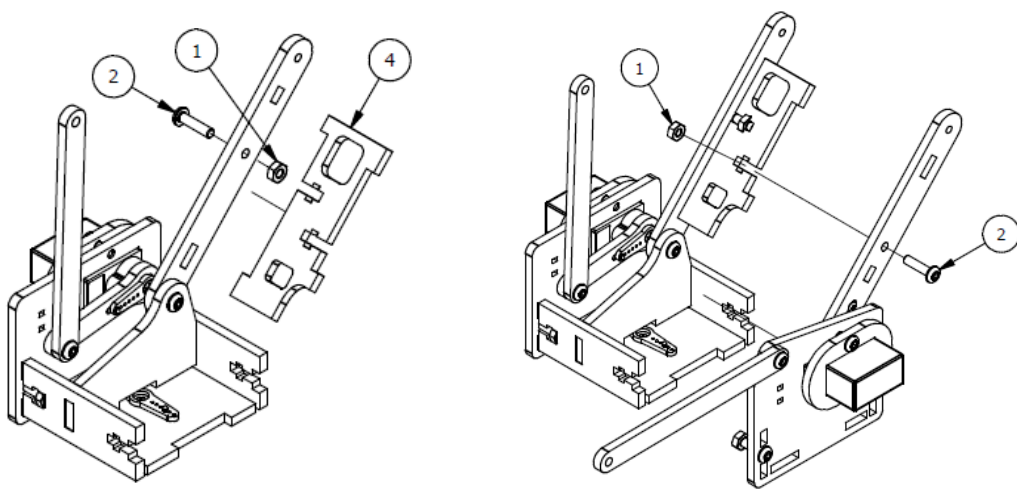
Шаг 2
Список деталей к Шагу 2
| Номер позиции | Количество | Название |
|---|---|---|
| 1 | 2 | М3 гайка |
| 2 | 1 | Крепление |
| 3 | 1 | Сервопривод |
| 4 | 2 | М3х8 винт |
| 5 | 1 | Основа левой руки |
| 6 | 1 | Параллельное крепление |
| 7 | 1 | Рычаг руки |
| 8 | 1 | М3×6мм винт |
| 9 | 1 | Серво рычаг |
| 10 | 2 | М3х12мм винт |
| 11 | 1 | Осевой серверный винт |
| 12 | 1 | Фиксирующий серверный винт |
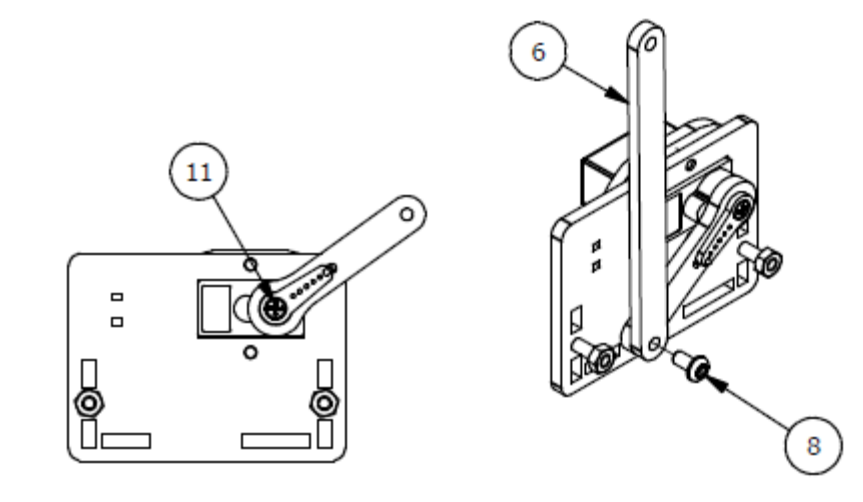
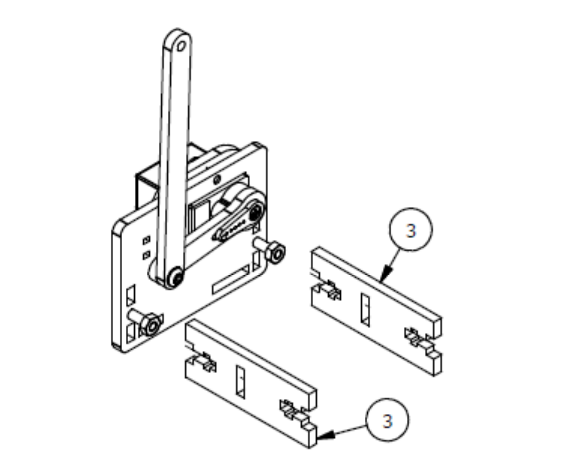
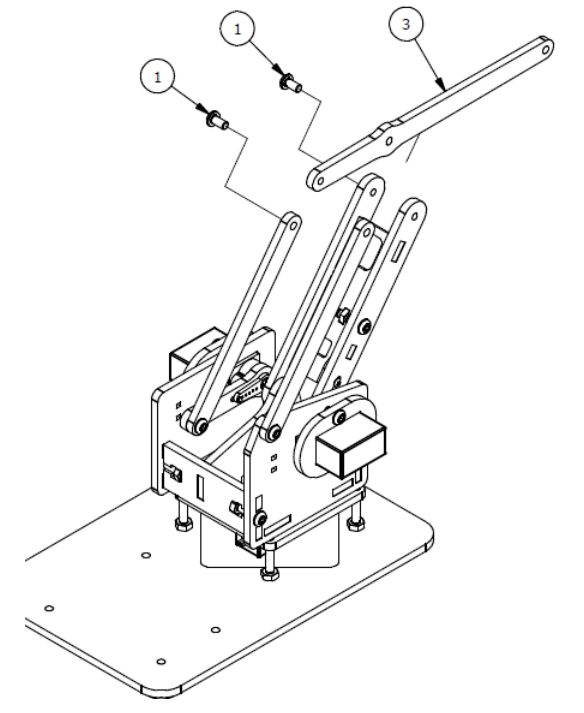
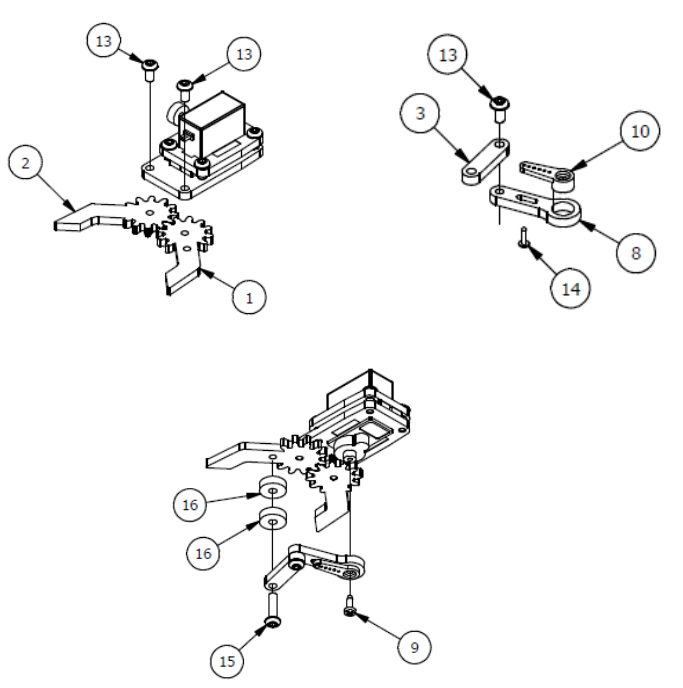
Шаг 3
Список деталей к Шагу 3
| Номер позиции | Количество | Название |
|---|---|---|
| 1 | 2 | М3 гайка |
| 2 | 1 | Крепление |
| 3 | 1 | Сервопривод |
| 4 | 2 | М3х8 винт |
| 5 | 1 | Параллельное крепление |
| 6 | 1 | М3х6мм винт |
| 7 | 1 | Серво рычаг |
| 8 | 2 | М3×6мм винт |
| 9 | 1 | Рычаг правой руки |
| 10 | 1 | Основание правой руки |
| 11 | 1 | Осевой серверный винт |
| 12 | 1 | Фиксирующий серверный винт |
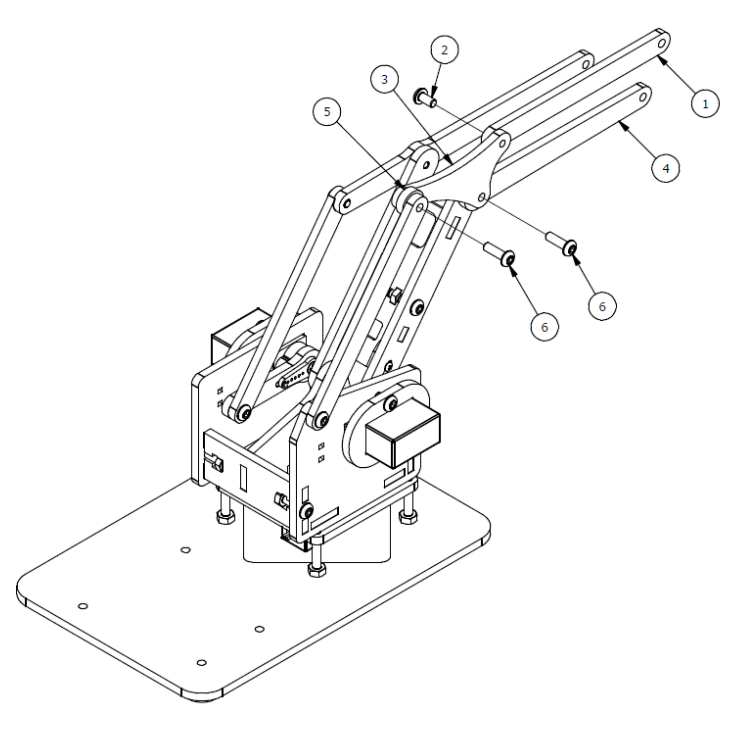
Шаг 4
Список деталей к Шагу 4
| Номер позиции | Количество | Название |
|---|---|---|
| 1 | 1 | Крепление вкладки левой руки |
| 2 | 1 | М3х6мм винт |
| 3 | 1 | Балка левой руки |
| 4 | 1 | Верхняя крышка |
| 5 | 1 | Двойной серво рычаг |
| 6 | 2 | Фиксирующий серверный винт. |
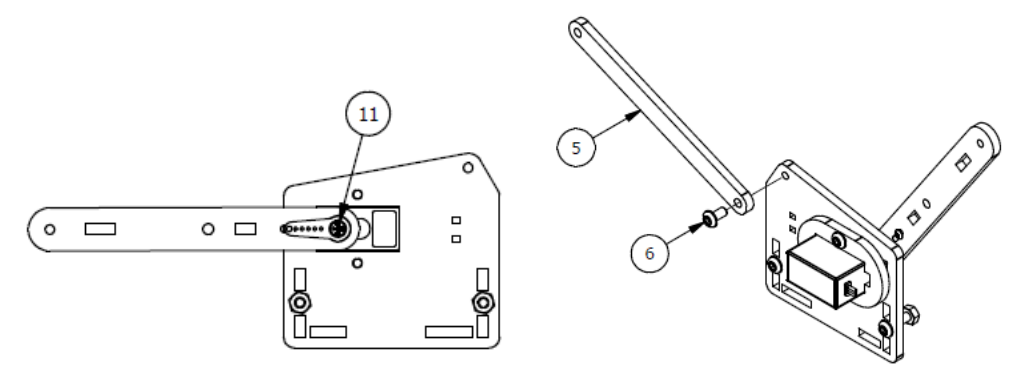
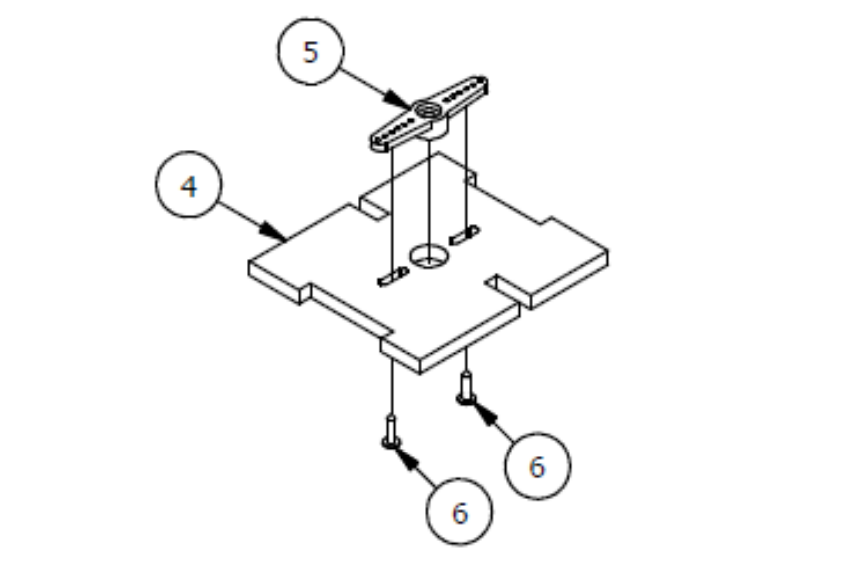
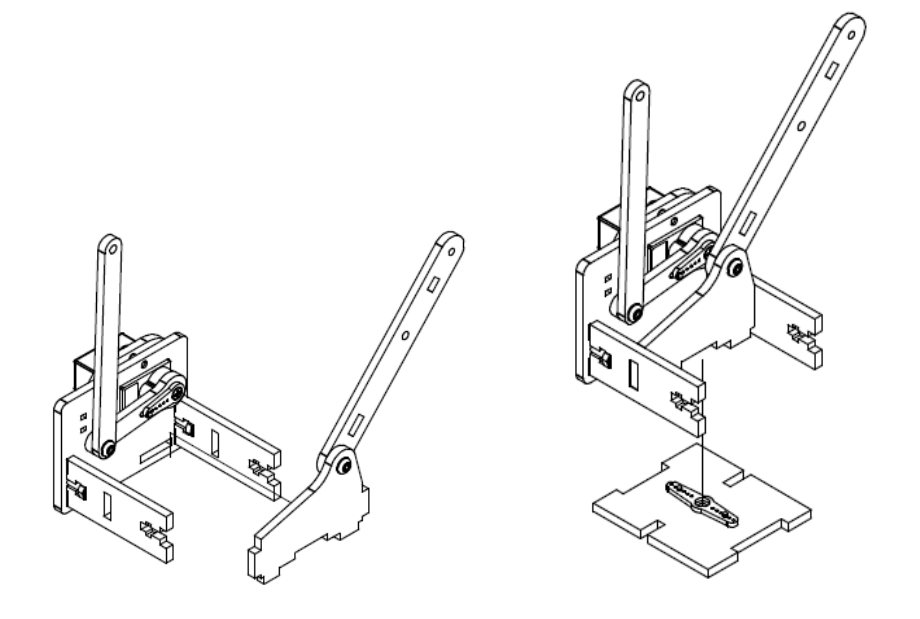
Шаг 5
Список деталей к Шагу 5
| Номер позиции | Количество | Название |
|---|---|---|
| 1 | 2 | М3 гайка |
| 2 | 2 | М3х12мм винт |
| 3 | 1 | Траверса основания манипулятора |
| 4 | 1 | Соединительное ребро жесткости |
Шаг 6
Список деталей к Шагу 6
| Номер позиции | Количество | Название |
|---|---|---|
| 1 | 2 | М3×6мм винт |
| 2 | 1 | Фиксирующий серверный винт |
| 3 | 1 | Балка левого запястья |
Шаг 7
Список деталей к Шагу 7
| Номер позиции | Количество | Название |
|---|---|---|
| 1 | 1 | Параллельная балка |
| 2 | 1 | М3х6мм винт |
| 3 | 1 | Коннектор |
| 4 | 1 | Балка правого запястья |
| 5 | 1 | Прокладка |
| 6 | 2 | M3x10 винт |
Шаг 8
Список деталей к Шагу 8
| Номер позиции | Количество | Название |
|---|---|---|
| 1 | 1 | Левый захват |
| 2 | 1 | Правый захват |
| 3 | 1 | Приводной рычаг |
| 4 | 1 | Левое крепление запястья |
| 5 | 1 | Правое крепление запястья |
| 6 | 1 | Нижнее крепление сервопривода |
| 7 | 1 | Верхнее крепление сервопривода. |
| 8 | 1 | Приводной рычаг |
| 9 | 1 | Осевой серверный винт. |
| 10 | 1 | Серво рычаг |
| 11 | 1 | Сервопривод |
| 12 | 4 | М3х8мм |
| 13 | 3 | М3х6мм |
| 14 | 1 | Фиксирующий серверный винт |
| 15 | 1 | М3х12мм винт |
| 16 | 2 | Прокладка |
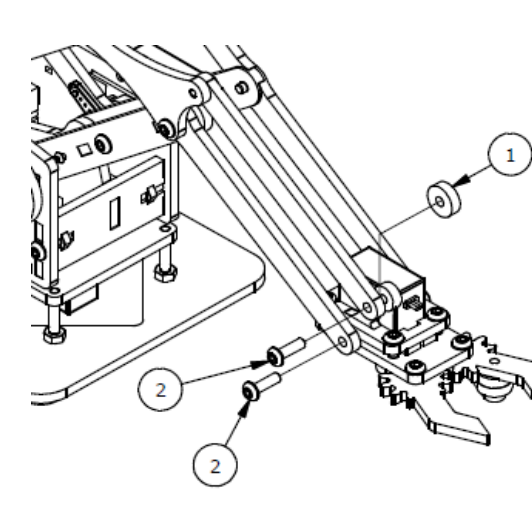
Шаг 9
Список деталей к Шагу 9
| Номер позиции | Количество | Название |
|---|---|---|
| 1 | 1 | Прокладка |
| 2 | 3 | М3х10мм винт |
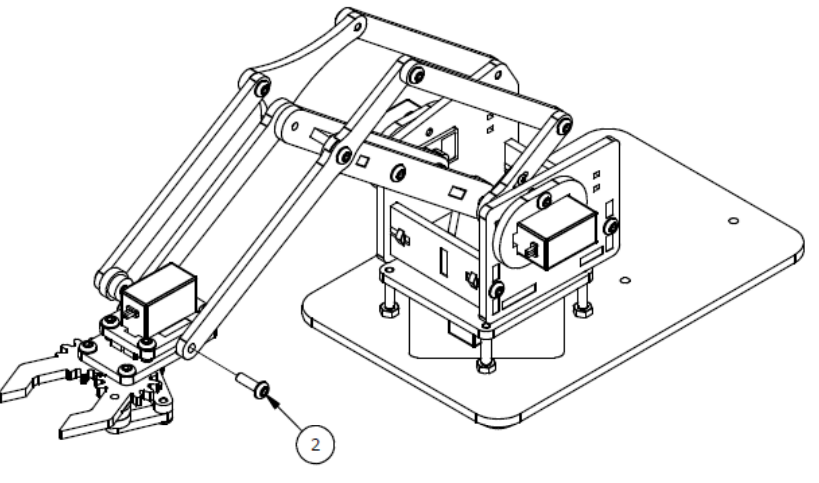
Вы можете скачать данную инструкцию по ссылке: Сборка робота-манипулятора. Часть 1
В собранном виде:

Точка роста / Школьный кванториум




Код товара: AR-RSK-WRS-02
Наличие: много

Образовательный набор для изучения многокомпонентных робототехнических систем и манипуляционных роботов.
Образовательный набор для изучения многокомпонентных робототехнических систем и манипуляционных роботов «Образовательный робототехнический комплект «СТЕМ Мастерская». Расширенный» предназначен для изучения робототехнических технологий, основ информационных технологий и технологий промышленной автоматизации, а также технологий прототипирования и аддитивного производства.
Полное описание
| Возраст | от 10 до 14 лет (Основное общее), от 14 до 18 лет (Среднее общее), от 18 лет |
| Классификация робототехники и конструкторов | Учебная робототехника, Роботы — манипуляторы |
| Артикул | AR-RSK-WRS-02 |
| Бренд | Прикладная робототехника |
| Страна производства | Россия |
| Умения и навыки | Программирование |
Подарок при покупке
Дарим подарок при покупке данного товара
Выбрать подарок
Весь товар сертифицирован
Подарки постоянным покупателям
Выгодные акции и спецпредложения
Сборка заказа 3 рабочих дня
Данное предложение не является публичной офертой и носит рекомендательный характер с целью подбора оптимальной комплектации оборудования. Комплектация оборудования может изменяться в соответствие с запросом Заказчика. Стоимость и состав предложения могут изменяться в соответствие с предложением Поставщика. Срок и условия поставки определяются индивидуально в зависимости от комплектации и количества запрашиваемого оборудования.


Комплектация
- Конструктивные элементы из металла для сборки модели манипуляционного робота с угловой кинематикой, 23 шт
- Конструктивные элементы из металла для сборки модели манипуляционного робота с плоско-параллельной кинематикой, 30 шт
- Конструктивные элементы из металла для сборки модели манипуляционного робота с DELTA кинематикой, 10 шт
- Крепежные элементы (винты различного номинала и длины), 64 шт
- Крепежные элементы (гайки различного номинала), 64 шт
- Элементы для создания шарнирных соединений, 7 шт
- Соединительные кабели различной длины, 7 шт
- Интеллектуальный сервомодуль с интегрированной системой управления, 7 шт
Сервомодуль представляет собой единый электромеханический модуль, включающий в себя привод на базе двигателя постоянного тока, понижающий редуктор, встроенную систему управления. Сервомодуль обладает интегрированной системой управления, обеспечивающей обратную связь, контроль параметров — положение вала, скорость вращения, нагрузка привода, а также обеспечивающей возможность последовательного подключения друг с другом и управления сервомодулями по последовательному полудуплексному асинхронному интерфейсу. Имеется режим постоянного вращения выходного вала.
Технические характеристики привода:
Нижняя граница диапазона допустимого напряжения питания — 9 В. Верхняя граница диапазона допустимого напряжения питания — 12 В. Передаточное отношение редуктора — 254. Максимальный момент — 1,5 Н*м. Нижняя граница диапазона номинальной скорости вращения в режиме постоянного вращения — 0 об/мин. Верхняя граница диапазона номинальной скорости вращения в режиме постоянного вращения — 59 об/мин. Максимальная величина угла поворота в режиме позиционного управления — 300 угловых градусов. Разрешающая способность — 0,29 угловых градусов. Размеры сервомодуля (ДхШхВ) — 32х50х40 мм. - Робототехнический контроллер, 1 шт
Робототехнический контроллер представляет собой модульное устройство, включающее в себя одноплатный микрокомпьютер для выполнения сложных вычислительных операций, периферийный контроллер для управления внешними устройствами и плату расширения для подключения внешних устройств. Модули робототехнического контроллера обладают одновременной конструктивной, аппаратной и программной совместимостью друг с другом. Имеется конструктивная, интерфейсная и электрическая совместимость робототехнического контроллера с опционально встраиваемым внешним микрокомпьютером.
Робототехнический контроллер обеспечивает возможность программирования с помощью средств языков С/С++, Python и свободно распространяемой среды Arduino IDE, а также управления моделями робототехнических систем с помощью среды ROS. Количество портов для подключения опционально встраиваемого внешнего микрокомпьютера — 48 шт. Имеется встроенный опциональный микрокомпьютер.
Технические характеристики робототехнического контроллера:
Нижняя граница диапазона питания внешней аккумуляторной батареи — 6,8 В. Верхняя граница диапазона питания внешней аккумуляторной батареи — 12 В. Порты для подключения внешних цифровых устройств — 16 шт. Порты для подключения внешних аналоговых устройств — 10 шт. Интерфейс 1-wire TTL для подключения по последовательному интерфейсу — 1 шт. Кол-во портов тип 4pin для подключения сервомодулей по последовательному интерфейсу — 2 шт. Программируемые кнопки — 1 шт. Интерфейс PWM — 1 шт. Интерфейс UART — 4 шт. Интерфейс I2C — 2 шт. Интерфейс SPI — 2 шт. Интерфейс для подключения микрофона — 1 шт. Интерфейс для подключения динамиков — 1 шт.
Технические характеристики встроенного опционального микрокомпьютера:
Количество вычислительных процессорных ядер — 4 шт. Оперативная память — 512 МБайт. Имеется встроенные интерфейсы WiFi и Bluetooth. Количество слотов для подключения карты памяти microSD — 1 шт. Встроенный микрофон — 1 шт. - Комплект для сборки пневмосистемы, 1 шт
Конструктивные элементы из пластика для сборки каркаса пневмосистемы — 2 шт. Крепежные элементы (винты, гайки, стойки, стяжки) — 30 шт. Коммутационные кабели (тип «Папа-Папа» и «Папа-Мама») — 10 шт. Коммутационная плата пневмосистемы, 1 шт.
Технические характеристики коммутационной платы пневмосистемы:
Количество линий +5В — 2 шт. Количество линий 0В — 2 шт. Количество выводов для коммутации силовой нагрузки с прямым управлением — 2 шт. Количество линий управления силовой нагрузкой — 2 шт. Количество индикаторов — 3 шт. Габариты — 43х33х12 мм.
Комплект вакуумного захвата — 1 шт. Технические характеристики комплекта вакуумного захвата:
Тип захвата — вакуумная присоска. Вакуумная присоска — 1 шт. Электромагнитный клапан — 1 шт. Вакуумный насос — 1 шт. Виниловая трубка — 1 м.
Напряжение питания — 5 В. Кнопочный выключатель с фиксацией — 1 шт. Коммутационный пневмосоединитель — 1 шт. - Универсальный вычислительный модуль, 1 шт
Универсальный вычислительный модуль представляет собой микропроцессорное устройство, предназначенное для управления устройствами, входящими в состав образовательного робототехнического комплекта. Имеется возможность подключения сервомодулей по последовательному интерфейсу. Интерфейс 1-wire TTL для подключения по последовательному интерфейсу — 1 шт. Размеры (ДхШ) — 40х40 мм. Нижняя граница диапазона допустимого напряжения питания — 5 В. Верхняя граница диапазона допустимого напряжения питания — 12 В. Объем Flash памяти — 256 Кбайт. Тактовая частота процессора — 16 МГц. Кол-во портов тип USB — 2 шт. Кол-во цифровых портов «Ввода-Вывода» — 12 шт. Кол-во аналоговых портов — 16 шт. Интерфейс UART — 1 шт. Интерфейс I2C — 1 шт. Интерфейс SPI — 1 шт. Линия питания «+12В» — 1 шт. Линия питания «+5В» — 1 шт. Линия питания «+3,3В» — 1 шт. Линия питания «Земля» — 1 шт. Светодиодный индикатор — 1 шт. Имеется беспроводной интерфейс WiFi и беспроводной интерфейс Bluetooth. Переключатель — 1 шт. Кнопка — 3 шт. - Плата расширения универсального вычислительного модуля, 1 шт
Плата расширения обеспечивает возможность подключения универсального вычислительного модуля к сети посредством интерфейса Ethernet. Габариты (ДхШ) — 40х40 мм. Напряжение питания — 5 В. Кол-во портов «Ввода-Вывода» — 40 шт. Интерфейс Ethernet — 1 шт. Интерфейс SPI — 1 шт. Интерфейс подключения карты microSD — 1 шт. Светодиодный индикатор — 4 шт. Кнопка — 1 шт. - Модуль технического зрения, 1 шт
Модуль технического зрения представляет собой вычислительное устройство со встроенным микроконтроллером, интегрированной телекамерой и оптической системой. Имеется возможность коммуникации с аналогичными модулями посредством шины на базе последовательного интерфейса с целью дальнейшей передачи результатов измерений группы модулей на управляющее вычислительное устройство, подключенное к данной шине. Встроенное программное обеспечение позволяет осуществлять настройку модуля технического зрения — настройку экспозиции, баланса белого, цветоразностных составляющих, площади обнаруживаемой области изображения, округлости обнаруживаемой области изображения, положение обнаруживаемых областей относительно друг друга.
Технические характеристики модуля технического зрения:
Размеры модуля (ДхШхВ) — 38х38х32 мм. Интерфейс USB для настройки модуля — 1 шт. Разрешение видеопотока, передаваемого по интерфейсу USB — 640х480 пикселей. Кол-во градаций цветовой палитры — 65536. Кол-во различных объектов, обнаруживаемых одновременно в секторе обзора модуля — 10 шт. Порт питания +5В — 2 шт. Порт тип GND «земля» — 2 шт. Интерфейс UART — 1 шт. Интерфейс I2C — 1 шт. Интерфейс SPI — 1 шт. Коммуникационный интерфейс 1-wire TTL для связи по последовательной шине — 1 шт. - Адаптер питания от сети 220 В, 1 шт.
- Сетевой кабель адаптера питания, 1 шт.
- USB интерфейсный кабель для программирования программируемого контроллера, 1 шт.
- Модуль тактовой кнопки, 3 шт
Размеры (ДхШ) — 12х12 мм. Интерфейсный разъем тип RJ14 — 1 шт. Интерфейс 1-wire TTL — 1 шт. Штыревой интерфейсный разъем — 1 шт. Количество линий штыревого интерфейсного разъема — 6 шт. Имеются цифровые и аналоговые порты. Имеется встроенный вычислительный микроконтроллер. Тактовая частота микроконтроллера — 16 МГц. Объем памяти, доступной по шине данных микроконтроллера — 8 КБайт. Нижняя граница диапазона допустимого напряжения питания — 5 В. Верхняя граница диапазона допустимого напряжения питания — 12 В. Размеры (ДхШ) — 40х26 мм. - Модуль светодиода, 3 шт
Размеры светодиода (ДхШ) — 3,5х2,8 мм. Интерфейсный разъем тип RJ14 — 1 шт. Интерфейс 1-wire TTL — 1 шт. Штыревой интерфейсный разъем — 1 шт. Количество линий штыревого интерфейсного разъема — 6 шт. Имеются цифровые и аналоговые порты. Имеется встроенный вычислительный микроконтроллер. Тактовая частота микроконтроллера — 16 МГц. Объем памяти, доступной по шине данных микроконтроллера — 8 КБайт. Нижняя граница диапазона допустимого напряжения питания — 5 В. Верхняя граница диапазона допустимого напряжения питания — 12 В. Размеры модуля (ДхШ) — 40х26 мм. - Модуль концевого прерывателя, 3 шт
Интерфейсный разъем тип RJ14 — 1 шт. Интерфейс 1-wire TTL — 1 шт. Штыревой интерфейсный разъем — 1 шт. Количество линий штыревого интерфейсного разъема — 6 шт. Имеются цифровые и аналоговые порты. Имеется встроенный вычислительный микроконтроллер. Тактовая частота микроконтроллера — 16 МГц. Объем памяти, доступной по шине данных микроконтроллера — 8 КБайт. Нижняя граница диапазона допустимого напряжения питания — 5 В. Верхняя граница диапазона допустимого напряжения питания — 12 В. Размеры (ДхШ) — 40х26 мм. - Модуль датчика цвета, 1 шт.
Количество цветовых каналов — 3 шт. Интерфейсный разъем тип RJ14 — 1 шт. Интерфейс 1-wire TTL — 1 шт. Штыревой интерфейсный разъем — 1 шт. Количество линий штыревого интерфейсного разъема — 6 шт. Имеются цифровые и аналоговые порты. Имеется встроенный вычислительный микроконтроллер. Тактовая частота микроконтроллера — 16 МГц. Объем памяти, доступной по шине данных микроконтроллера — 8 КБайт. Нижняя граница диапазона допустимого напряжения питания — 5 В. Верхняя граница диапазона допустимого напряжения питания — 12 В. Размеры (ДхШ) — 40х26 мм. - Модуль RGB светодиода, 3 шт.
Количество цветовых каналов — 3 шт. Интерфейсный разъем тип RJ14 — 1 шт. Интерфейс 1-wire TTL — 1 шт. Штыревой интерфейсный разъем — 1 шт. Количество линий штыревого интерфейсного разъема — 6 шт. Имеются цифровые и аналоговые порты. Имеется встроенный вычислительный микроконтроллер. Тактовая частота микроконтроллера — 16 МГц. Объем памяти, доступной по шине данных микроконтроллера — 8 КБайт. Нижняя граница диапазона допустимого напряжения питания — 5 В. Верхняя граница диапазона допустимого напряжения питания — 12 В. Размеры (ДхШ) — 40х26 мм. - Программное обеспечение для визуализации 3D моделей манипуляционного робота
Программное обеспечение обеспечивает трехмерную визуализацию модели манипуляционного робота (с угловой, плоскопараллельной и дельта-кинематикой) в процессе работы, обеспечивать построение пространственной траектории движения исполнительного механизма манипуляционного робота, возможность задания последовательности точек для прохождения через них исполнительного механизма манипуляционного робота. Программное обеспечение функционирует, как в отдельности в виде среды моделирования, так и в режиме мониторинга в реальном времени при подключении модели манипулятора посредством робототехнического контроллера. Программное обеспечение обеспечивает возможность построения графиков заданных и текущих обобщенных координат манипуляционного робота, графиков значений скоростей и ускорения, графиков расчетных значений нагрузки. Программное обеспечение позволяет задавать последовательность передвижений манипулятора посредством набора команд в блочно-графическом интерфейсе. - Учебное пособие на русском языке, 2 шт
В состав набора входит учебный комплект, включающий в себя учебное пособие, набор библиотек трехмерных элементов для прототипирования моделей манипуляционных роботов, а также программное обеспечение для работы с набором. Учебное пособие содержит материалы по разработке трехмерных моделей мобильных роботов, манипуляционных роботов с различными типами кинематики (угловая кинематика, плоско-параллельная кинематика, дельта-кинематика, SCARA (рычажная кинематика), платформа Стюарта), инструкции по проектированию роботов, инструкции и методики осуществления инженерных расчетов при проектировании (расчеты нагрузки и моментов, расчет мощности приводов, расчет параметров кинематики), инструкции по разработке систем управления и программного обеспечения для управления роботами, инструкции и методики по разработке систем управления с элементами искусственного интеллекта и машинного обучения.
На начальном этапе учащиеся могут разрабатывать модели роботов и программировать их с использованием блочно-графической среды программирования.
На среднем этапе учащиеся могут программировать модели роботов с использованием среды программирования Arduino IDE, используя отечественный робототехнический контроллер.
В рамках начального и среднего этапа учащиеся могут применять аддитивные технологии в процессе разработки и изготовления конструкции робота. Начиная с начального этапа, учащиеся могут также разрабатывать модели автономных роботов с использованием различных сенсорных устройств, в том числе систем технического зрения на базе отечественного модуля.
В рамках старшего этапа учащиеся могут расширить функционал программируемого контроллера за счет установки модуля расширения на базе микрокомпьютера с ОС Linux. Благодаря этому появляется возможность изучать основы разработки робототехнических систем с системами управления на базе ОС реального времени или типа Linux, а также изучать методы сбора и анализа визуальной информации, принципы дистанционного управления и интеграции робототехнических комплексов в системы типа Индустрия 4.0 и Интернет Вещей.
�� ��������� ����������� ������� ��������� � ������ �������� �������� ������� �� ������ ��������, ����� ���� ������� �������� ����������� �������� �� ���������� ����.
�������� �� ������
�������� (��-��). ������ �������� ����� � ���� ������ � 18 �� 21.00 (��� �������, ��� ����� ����������� �� 18.00), ���� ������� ���������� ��� (���� ����� ����������� ����� 18.00).
�����������
�� ������ ������� ���������� �� ����� ����� � ����� ���� � ������� ��� �����. ���� ������ � ���������� ������� �������� ����� ������ �����. ��������������� ����� ����� ���������� ��� � ������� ���� ������� ����.
Запросить консультацию о товаре

- Все товары категории
- Все товары бренда Прикладная робототехника
Учебный манипулятор реализован на основе интеллектуальных сервомодулей Dynamixel и специализированной системы управления. Благодаря применению высококачественных сервомодулей Dynamixel, применяемых в профессиональной деятельности в сфере робототехники, учебный манипулятор обладает повышенной точностью и повторяемостью позиционирования исполнительного органа (схвата) по сравнению с какими-либо другими учебными моделями. Наличие встроенной системы управления сервомодулей Dynamixel и множества обратных связей обеспечивает возможность гибкой настройки и управления манипулятором в процессе его работы.
Для управления манипуляционным роботом применяется модульный робототехнический контроллер, что обеспечивает возможность модернизации и расширения функциональных возможностей. Представленные ниже технические особенности позволяют применять данный манипуляционный РТК для разработки макета производственной линии, применяемого в рамках соревнований .
Технические особенности:
- Сбалансированные оси вращения с подшипниковыми узлами.
- Наличие крепежа для модуля технического зрения на схвате манипулятора.
- Манипуляционный РТК выполнен на базе сервомодулей Dynamixel: МХ-64Т – 2 шт, МХ-28Т – 2 шт, АХ-12А – 2 шт (или сервомодули Dynamixel с более лучшими техническими характеристиками).
- Радиус зоны сервиса — не менее 30 см.
- Номинальная грузоподъемность – 250 грамм.
- Грузоподъемность – 450 грамм, в зависимости от ориентации схвата в кратковременном режиме.
- Максимальная грузоподьемность – до 800 грамм в кратковременном режиме.
- Для управления РТК используется программируемый контроллер STEM Board c возможностью встраивания модулей расширения:
— Программируемый контроллер OpenCM – наличие,
— Встраиваемый одноплатный микрокомпьютер – отсутствует (приобретается опционально). - Наличие сетевого адаптера для питания от сети 220В.
- Наличие интерфейсного кабеля для программирования.
- Поставляется в деревянном боксе для хранения и транспортировки.
- Гарантия – 6 месяцев.
Учебный манипулятор обладает встроенным программным обеспечением для коммуникации с облачным сервером РТС ThingWorx, применяемым для разработки приложений с использованием технологий «Интернет вещей». Встроенная система управления учебного манипулятора обеспечивает возможность объединения аналогичных учебных моделей в единую информационную систему для управления группой роботов в рамках решения учебной технологической задачи.
Манипуляторы с угловым типом кинематической схемы могут применяться для свободного перемещения рабочего инструмента в пространстве в рамках сферической рабочей зоны относительно системы координат основания. В большинстве случаев подобные манипуляторы применяются для выполнения задач по перемещению и точному позиционированию объектов, обработки пространственных контуров и поверхностей. Данный тип кинематики является наиболее распространенным в промышленности в области машиностроения и механической обработки, сварочных и покрасочных работ.
Учебный манипулятор представляет собой доступную учебную модель промышленного манипуляционного робота, обеспечивающую возможность на практике изучить большинство аспектов разработки систем управления манипуляционных роботов с угловым типом кинематики, а базовых принципов применения робототехники при автоматизации технологических процессов.