[email protected]
Введение
Цель данного пособия – познакомить читателя с основами проведения эконометрических исследований в среде GRETL. Основная аудитория данной книги – студенты бакалавриата, обучающиеся по направлениям «Экономика», «Бизнес-информатика», «Управление персоналом», «Менеджмент», однако она может быть полезна и студентам других направлений, а также представителям бизнес-сообщества, которые по роду своей деятельности столкнулись с необходимостью проведения эконометрических исследований. Данное учебное пособие – это попытка практического изложения основ эконометрики с минимальными теоретическими выкладками, при этом предполагается, что недостаток теоретических знаний должен быть восполнен читателем самостоятельно с помощью учебников по основам эконометрики. Для обеспечения связи практических навыков с теоретическими знаниями в области эконометрики ко всем рассматриваемым темам даются ссылки на литературу. При этом основная задача данного пособия – помочь читателю в освоении эконометрики, изложить некоторые технические аспекты проведения исследований с использованием среды GRETL. Почему именно GRETL? Данный эконометрический пакет является бесплатным программным продуктом, который, с одной стороны, доступен любому пользователю, а с другой – обладает достаточно обширными возможностями для анализа данных и проведения эмпирических исследований. Немаловажным является и то, что в GRETL имеется значительный пул данных из большинства классических зарубежных учебников по основам эконометрики, что позволит достаточно легко переключиться с простейших примеров, рассмотренных в данном пособии, на более сложные содержательные задачи и кейсы из учебников.
В данном пособии весь материал излагается с точки зрения практики – то есть все основные разделы курса эконометрики для бакалавриантов даны в примерах и задачах. Поскольку невозможно приобрести навык проведения эконометрических расчетов, только изучая учебник, предполагается, что читатель должен иметь возможность проделать все излагаемые действия на практике. С этой целью в пособии использовались данные из учебника J. M. Wooldridge «Basic econometrics», которые доступны в GRETL. Все наборы данных при первом обращении к ним в пособии обозначены ссылками и указателями на источник.
Перед тем как начать осваивать основы эконометрики в среде GRETL, необходимо скачать и установить на свой компьютер сам статистический пакет. Он доступен по ссылке http://GRETL.sourceforge.net/. Вся информация о том, как установить GRETL, приводится на сайте, поэтому нет нужды в подробном изложении, стоит лишь сказать, что программа имеет версию как под ОС Windows, так и под Mac OS, а также что библиотеки данных должны быть установлены отдельно, для этого нужно перейти по ссылке http://GRETL.sourceforge.net/GRETL_data.html.
Удачи в проведении интересных, содержательных и полезных эконометрических исследований!
1. Линейная регрессионная модель
Для начала введем некоторые обозначения. Предположим, что некоторая величина Y зависит от величин . Введем понятие регрессионного уравнения – это уравнение вида , где . Через n обозначим число наблюдений, по которым строится регрессия, k – число регрессоров в модели, – случайная величина, которая носит название ошибки регрессии.
Модель такого вида называется классической линейной регрессионной моделью (ЛРМ) в случае, если выполняются следующие предпосылки:
1. , – линейная спецификация модели, где – коэффициенты модели, которые подлежат определению, , – ошибки модели.
2. , – детерминированные величины.
3. – математическое ожидание ошибок равно нулю, , дисперсия ошибок не зависит от номера наблюдения.
4. , – совместное математическое ожидание ошибок разных наблюдений равно нулю.
5. Если выполняется дополнительная предпосылка о нормальном распределении ошибок , то классическая линейная регрессионная модель называется нормальной линейной регрессионной моделью (НЛРМ).
Подробнее о предпосылках линейной регрессионной модели можно прочесть в [2, 3].
2. Оценка линейной регрессионной модели
Рассмотрим множественную линейную регрессию
, ,
где – средний уровень заработной платы в час в долларах, – образование в годах, – общий стаж работы в годах, – опыт работы у текущего работодателя, в годах, – ошибка регрессии, n – число наблюдений [файл с данными wage1.gdt].
Для того чтобы оценить предложенную модель по методу наименьших квадратов (МНК), используем команду меню Модель – Метод наименьших квадратов.
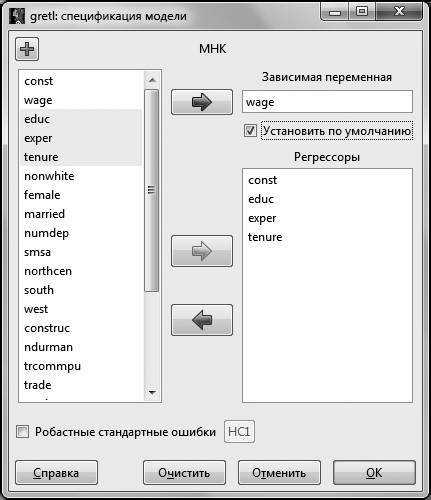
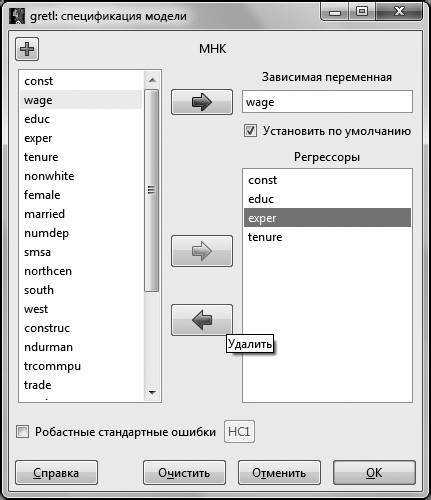
В появившемся диалоговом окне в поле Зависимая переменная помещаем переменную (для этого выделяем ее курсором в списке переменных и нажимаем на стрелку, соответствующую окну Зависимая переменная. Данный способ перемещения переменных справедлив для всех операций с диалоговыми окнами).
Для дальнейшего удобства можно поставить галочку в окошке Установить по умолчанию. Это делается для того, чтобы при изменении спецификации исследуемой модели зависимая переменная не менялась. В окно Регрессоры
отправляем регрессоры модели – это переменные , , .
Рис. 2.1
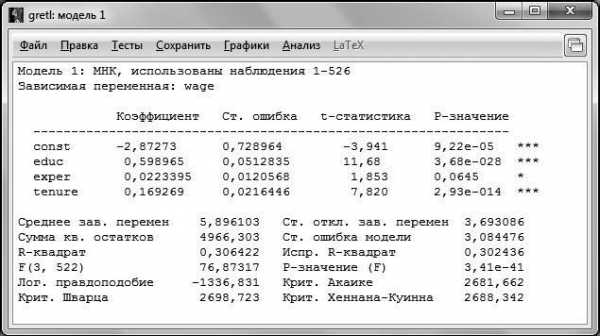
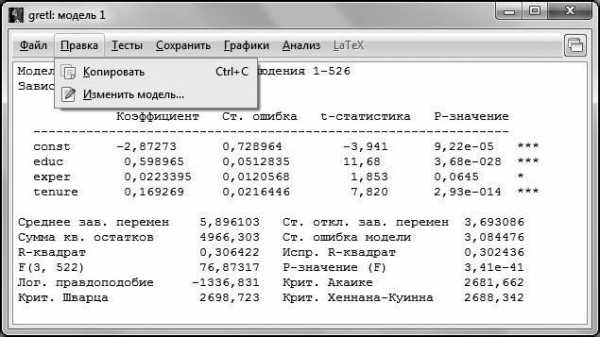
После этого нажимаем ОК. В результате коэффициенты модели были оценены методом наименьших квадратов. Результат оценки представлен на рис. 2.2.
Рис. 2.2
Для того чтобы понимать, какие результаты позволяет получить GRETL, разберем информацию, представленную на распечатке по строкам сверху вниз.
В первой строке указывается метод оценки и количество наблюдений, по которым производилась оценка. Достаточно часто случается, что количество наблюдений, по которым производилась оценка, не совпадает с числом наблюдений в исходной выборке, даже если она не была ограничена. Это может быть связано, например, с наличием пропусков в данных.
Вторая строка напоминает нам о том, какая переменная была выбрана в качестве зависимой.
После двух первых строк следуют подтаблицы непосредственно с результатами оценивания. В первой подтаблице указаны регрессоры, включенные в модель, напротив каждого из них указывается его коэффициент (столбец Коэффициенты), стандартная ошибка оценки коэффициента (столбец Ст. ошибка), значение статистики Стьюдента для коэффициента (столбец t-статистика) и вероятность ошибки I рода (столбец P-значение). Стоит отметить, что константа тоже является регрессором, и для нее также рассчитываются все указанные характеристики.
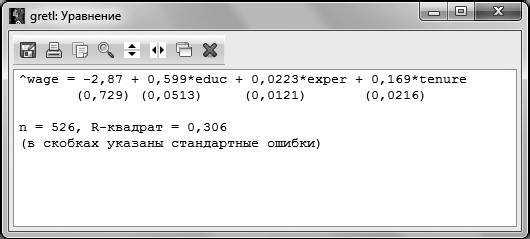
По распечатке, представленной на рис. 2.2, мы можем выписать получившееся уравнение регрессии:
Аналогично можно получить оцененное уравнение и в GRETL, для этого выбираем в меню регрессии Файл – Просмотреть как уравнение.
Рис. 2.3
Однако для того, чтобы иметь возможность дать интерпретацию коэффициентам регрессии и строить прогнозы, необходимо проверить, является ли полученная модель адекватной.
Для этого, в свою очередь, необходимо провести ряд эконометрических тестов, а именно проверить значимость регрессии в целом, значимость отдельных коэффициентов регрессии, оценить качество полученного регрессионного уравнения. Вообще говоря, перед проверкой значимости и качества уравнения необходимо провести тесты на выполнение основных предпосылок линейной регрессионной модели (гомоскедастичность, отсутствие автокорреляции). На данном этапе мы будем считать эти тесты проведенными и вернемся к вопросам выполнения предпосылок ЛРМ позднее.
3. Тест Фишера (Fisher test)
Для начала проверим гипотезу о незначимости регрессии в целом. Тест позволит понять, является ли построенная модель адекватной с точки зрения статистики. Для этой цели воспользуемся тестом Фишера [3].
Сформулируем гипотезы для проверки незначимости регрессии в целом в рассматриваемом примере [
файл с данными wage1.gdt] модели , :
как минимум один из коэффициентов отличен от нуля.
Для принятия решения о том, какую гипотезу нужно отвергнуть, построим F-статистику. Для этого нам должны быть известны (помимо уже имеющихся параметров n – объем выборки и k – число регрессоров в модели) величины RSS и ESS. В явном виде в распечатке на рис. 2.2 дано значение ESS – сумма квадратов остатков, которая составляет ESS = 4966,3, а также из распечатки известен коэффициент детерминации (подробнее о коэффициенте детерминации и его интерпретации можно прочесть в § 7).
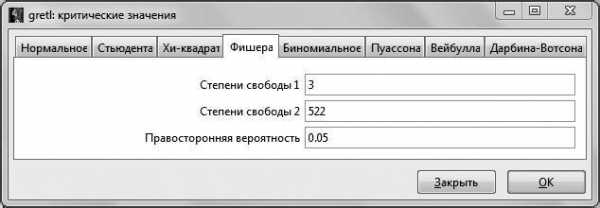
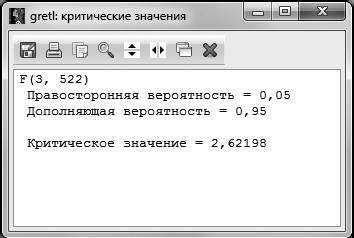
Если вспомнить, что ,1 а , то можно путем простых алгебраических преобразований найти необходимую нам величину RSS. При этом . Отсюда можно вычислить . Критическое значение F-статистики возьмем на уровне значимости 5 %: (чтобы получить это значение, в основном меню
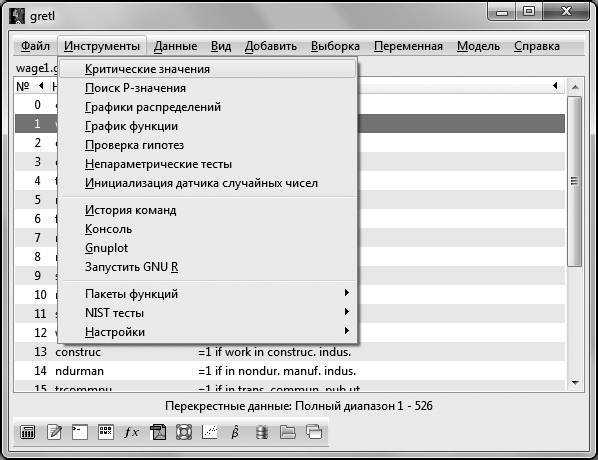
GRETL нужно выбрать Инструменты – Критические значения – Фишера и ввести необходимое число степеней свободы и правостороннюю вероятность либо посмотреть в статистических таблицах распределения Фишера для уровня значимости 5 %, например в [7]).
Рис. 3.1
Рис. 3.2
Уровень значимости, на котором принимается решение о том, какую гипотезу не отвергать, остается на усмотрение исследователя. Как правило, если нет представления, какой именно уровень значимости брать, предлагается выбирать 5 %. В случаях работы с маленьким по объему выборками (от 30 до 100 наблюдений) предлагается брать уровень значимости 10 %. Для больших выборок (более 1000 наблюдений) можно взять уровень значимости 1 %. В нашем случае объем выборки средний (526 наблюдений, эта информация дана в первой строке распечатки на рис. 2.2.), поэтому можно было принять .
Сравниваем расчетное значение F-статистики с критическим , то есть 78,2 > 2,6. Следовательно, можно сделать вывод, что гипотеза о незначимости регрессии в целом отвергается.
Тест Фишера можно провести также в полуавтоматическом режиме и в автоматическом режиме. Полуавтоматический режим состоит в том, что нам не нужно вручную вычислять значение расчетной F-статистики, оно дано в распечатке на рис. 2.2. В этом случае нужно лишь выяснить критическое значение F-статистики и сравнить расчетное значение с критическим.
В автоматическом режиме нужно также воспользоваться распечаткой GRETL и посмотреть на р-значение статистики Фишера на рис. 2.2 (в распечатке р-значение (F)). В р-значении содержится вероятность ошибки I рода. Таким образом, р-значение (F) для теста Фишера – это вероятность ошибки I рода при тестировании гипотезы . По существу это вероятность ошибиться, отвергнув гипотезу
H0. Для принятия решения, можно ли отвергнуть гипотезу H0, нужно сравнить р-значение с заданным уровнем значимости a. Уровень значимости задает вероятность ошибки I рода, то есть, грубо говоря, какую долю ошибок мы готовы себе позволить, отвергнув гипотезу H0. Если р-значение меньше принятого уровня значимости, то маловероятно, что мы ошибемся, отвергая гипотезу H0 в ситуации, когда р-значение больше уровня значимости, вероятна ошибка в случае отклонения нулевой гипотезы, поэтому ее стоит принять. Отсюда можно сделать вывод, что р-значение показывает вероятность ошибиться, отвергнув гипотезу H0, при том, что она верна. Эта интерпретация р-значения справедлива для всех статистических тестов, и мы будем иметь ее в виду в дальнейшем. В данном случае р-значение (F) (р-значение (F) в распечатке представляет собой «
3,41e-41» – это компьютерный способ записи числа , которое практически равно 0). Это говорит о том, что можно отвергнуть гипотезу H0 (вероятность ошибки близка к 0).
Стоит обратить внимание еще на один полезный факт. При расчете F-статистики вручную мы использовали формулу . Используя соотношение , можно переписать расчетную статистику через коэффициент детерминации, не используя квадраты остатков .
4. Тест Стьюдента (t-test)
После того как мы проверили незначимость регрессионного уравнения в целом, рассмотрим, как проверять незначимость коэффициентов при отдельных регрессорах. Для этой цели воспользуемся тестом Стьюдента [3].
Проверим незначимость коэффициента при переменной . Сформулируем гипотезы теста для указанной переменной [файл с данными wage1.gdt]. Они будут выглядеть следующим образом:
Значение оцененного коэффициента при этой переменной находится в столбце «
Коэффициент» – . Для того чтобы вычислить расчетную t-статистикy, необходимо знать значение стандартной ошибки для коэффициента, оно содержится в столбце «Ст. ошибка». Для переменной стандартная ошибка . Отсюда можем вычислить . Для принятия решения о том, можно ли отвергнуть гипотезу H0, сравним значение с критическим значением статистики . Примем уровень значимости . Как уже было сказано, объем выборки составляет 526 наблюдений, то есть n = 526. Число регрессоров в модели составляет 4 (константа тоже регрессор), то есть, k = 4. Отсюда следует, что нужно искать критическое значение из двустороннего распределения Стьюдента на уровне значимости 5 % (одностороннее распределение 2,5 %) с 522 степенями свободы. Для поиска критического значения из распределения Стьюдента можно воспользоваться статистическими таблицами, например из [7]. Но можно воспользоваться возможностями GRETL. Для этого в основном меню выберем
Инструменты – Критические значения.
Рис. 4.1
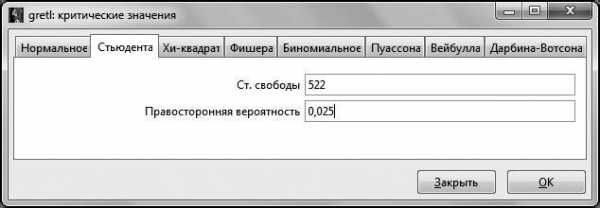
В открывшемся окне «Критические значения» выберем вкладку, соответствующую распределению Стьюдента, и введем нужные параметры распределения.
Рис. 4.2
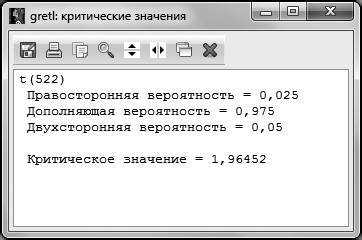
Стоит обратить внимание на то, что в GRETL предполагается для распределения Стьюдента вводить не двустороннюю вероятность, а только правостороннюю вероятность, то есть в нашем случае это 2,5 %. После нажатия клавиши ОК получаем искомое критическое значение .
Рис. 4.3
После этого сравниваем расчетное и критическое значение статистик для переменной . В нашем случае (|11,68 | > 1,96), отсюда можно сделать вывод, что гипотеза H0 отвергается, то есть можно говорить о том, что регрессор значим.
Рассмотренный способ проверки гипотезы незначимости коэффициента при отдельном регрессоре позволяет соотнести теоретические знания о проверке незначимости с практикой. Однако ту же самую процедуру можно несколько упростить. Обратим внимание, что в столбце t-статистика для всех переменных уже указаны расчетные значения статистики. Так, например, для переменной указано полученное нами значение . Это несколько сокращает процедуру проверки, однако сравнение расчетного и критического значения t-статистики все же приходится проделывать самостоятельно.
Существует еще более простой и быстрый способ проверки незначимости коэффициента.
В рассматриваемом примере p-значение переменной составляет , то есть практически равно 0. В этом случае, p-значение переменной меньше заданного уровня значимости . Это значит, что можно отвергнуть гипотезу H0, то есть коэффициент при регрессоре значим.
Аналогичную проверку незначимости мы можем провести для коэффициентов остальных регрессоров. На 5 %-ном уровне значимости можно утверждать, что коэффициент при и константа – значимы, коэффициент при на 5 %-ном уровне не значим, однако он является значимым на 10 %-ном уровне значимости.
В программе GRETL предусмотрена визуализация значимости коэффициентов при отдельных регрессорах на разных уровнях значимости. Для этого справа от каждого регрессора расположены звездочки:
• Наличие одной звездочки говорит о том, что коэффициент значим только на 10 %-ном уровне.
• Наличие двух звездочек говорит о значимости коэффициента на 5 %-ном уровне.
• Три звездочки информируют о значимости коэффициента на 1 %-ном уровне.
• Отсутствие звездочек говорит о незначимости коэффициента на 10 %-ном уровне.
Мы проверили незначимость коэффициентов при всех регрессорах, включенных в модель. Если мы хотим ориентироваться на 5 %-ный уровень значимости, то нужно удалить переменную с незначимым коэффициентом. Для того чтобы это сделать в окне с построенной моделью (в нашем случае это окно Модель 1, но, вообще говоря, это может быть Модель № в зависимости от того, сколько вы моделей построили до этого), выбираем пункт меню Правка – Изменить модель.
Рис. 4.4
В открывшемся окне выделяем переменную и красной стрелкой удаляем ее из независимых переменных.
Рис. 4.5
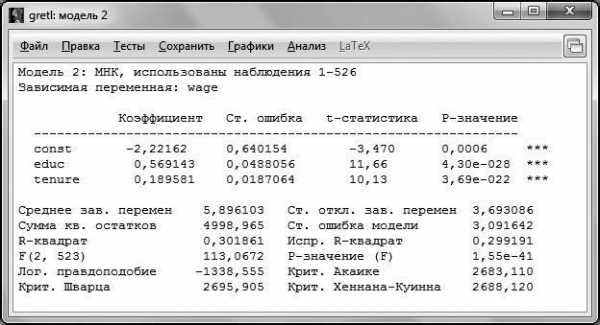
Обновленная модель представлена на рис. 4.6.
Рис. 4.6
Как видно из распечатки, все коэффициенты регрессии в обновленной модели значимы на 1 %-ном уровне (следовательно, и на 5 %-ном уровне они тоже значимы). Возможности t-теста не ограничиваются только проверкой незначимости коэффициентов при регрессорах. На самом деле проверка незначимости коэффициента является частным случаем проверки равенства коэффициента при регрессоре конкретному значению [2, 3].
Разберем это на примере. Проверим, а можем ли мы округлить коэффициент при переменной до 0,2. Сформулируем гипотезы для проверки этого предположения:
Для проверки такого рода гипотезы уже нельзя воспользоваться рассчитанным в GRETL значением t-статистики, а также р-значением, поэтому вычислим значение t-статистики для переменной самостоятельно: . Значение критической точки Стьюдента составит .
Сравниваем расчетную статистику и критическую и получаем, что , то есть (|–0,56 | < 1,96). В этом случае, мы можем принять нулевую гипотезу и округление коэффициента перед до 0,2 будет статистически корректно. Аналогичные гипотезы мы можем проверять для остальных коэффициентов регрессии.
Проверить, может ли коэффициент при регрессоре равняться заданному значению, позволяет также доверительный интервал [2, 3].
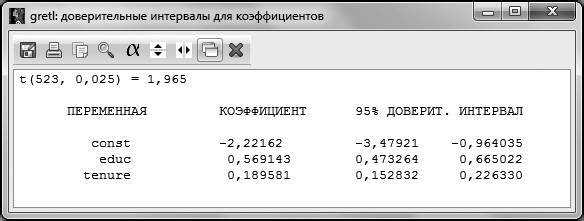
Используя данные из распечатки на рис. 4.6, можно построить доверительные интервалы для всех коэффициентов самостоятельно либо воспользоваться встроенной функцией GRETL для построения доверительного интервала.
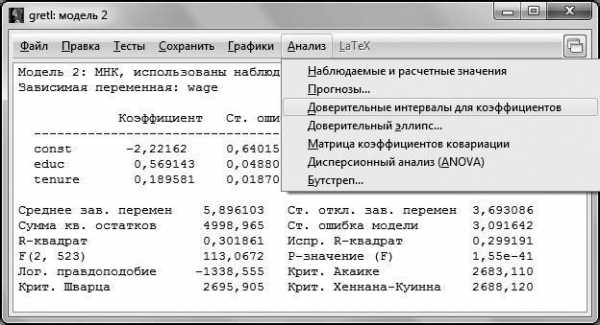
Для этого в окне модели вызовем пункт меню Анализ – Доверительные интервалы для коэффициентов.
Рис. 4.7
Результатом работы данной функции является следующее окно (рис. 4.8).
Рис. 4.8
Истинное значение коэффициента при переменной с вероятностью 95 % накрывается интервалом .
Нужно обратить внимание на то, что с помощью доверительного интервала можно проверять незначимость коэффициентов при регрессорах. В случае, если доверительный интервал накрывает 0 (то есть истинное значение коэффициента может принимать нулевое значение), можно сделать вывод о том, что коэффициент не значим.
Еще одна возможность для проверки гипотез с помощью теста Стьюдента – это односторонние гипотезы [2, 3].
Разберем, как проводится односторонний t-тест на примере. Проверим, верно ли, что коэффициент перед переменной можно считать большим 0,2.
Значение расчетной статистики для этого теста будет такое же, как и в предыдущем тесте (проверка равенства коэффициента заданному значению). Критическая точка составит . Сравнивая расчетное значение статистики с критическим, получаем , то есть –0,56 < 1,65. Значит, гипотеза H0 принимается.
По сути, все разновидности t-теста и построение доверительного интервала для коэффициента – это две стороны одной медали. Полезные результаты можно получать и тем и другим способом, выбор способа ответа на вопросы о незначимости коэффициента при регрессоре и соотношения коэффициента регрессора с заданным значением возлагается на исследователя.
fictionbook.ru
Общие сведения о пакете GRETL — Студопедия.Нет
Министерство образования и науки Украины
Севастопольский национальный технический университет
РЕАЛИЗАЦИЯ ЭКОНОМЕТРИЧЕСКИХ МЕТОДОВ
ОБРАБОТКИ ФИНАНСОВО-ЭКОНОМИЧЕСКОЙ ИНФОРМАЦИИ В GRETL 1.7.1
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к лабораторному практикуму
по дисциплине «Эконометрия»
для студентов специальности
6.050201 — «Менеджмент организаций»
всех форм обучения
Севастополь
2008
УДК 658
«Реализация эконометрических методов обработки финансово-экономической информации в GRETL 1.7.1»
методические указания к выполнению лабораторных работ по дисциплине «Эконометрия» для студентов специальности 8.050201 – «Менеджмент организаций» всех форм обучения / Сост. А.В. Цуканов, Т.А. Кокодей. – Севастополь: Изд-во СевНТУ, 2008г. – 135 с.
Целью методических указаний являетсяполучение практических навыков построения эконометрических моделей при изучении экономических явлений и процессов с использованием системы Gretl 1.7.1.
Методические указания утверждены на заседании кафедры менеджмента и экономико-математических методов, (протокол № 5 от 23.01.2008 г.).
Допущено учебно-методическим центром СевНТУ в качестве методических указаний.
Рецензент:
Фисун С.Н., канд. техн. наук, доцент кафедры «Кибернетика и вычислительная техника».
СОДЕРЖАНИЕ
| Лабораторная работа №1. Введение в пакет программ GRETL 1.7.1………… | 5 |
| 1. Цель работы……………………………………………………………………………… | 5 |
| 2. Теоретический раздел……………………………………………………………… | 5 |
| 2.1. Общие сведения о пакете Gretl………………………………………………….. | 5 |
| 2.2. Стартовый экран Gretl…….……………………………………………………… | 6 |
| 2.3. Построение набора статистических данных………………………………………… | 7 |
| 2.3.1. Ручной ввод информации с клавиатуры……………………………………… | 8 |
| 2.3.2. Импорт данных…………………………………………………………………. | 10 |
| 2.4.Открытие встроенного или ранее созданного набора данных………………… | 11 |
| 2.5 Редактирование набора статистических данных…………………………………….. | 12 |
| 2.6. Экспорт данных………………………………………………………………….. | 15 |
| 3. Порядок выполнения лабораторной работы…………………………………….. | 16 |
| 4. Содержание отчета о выполнении лабораторной работы………………………. | 17 |
| Библиографический список………………………………………………………….. | 18 |
| Лабораторная работа №2. Линейный регрессионный анализ взаимосвязи статистических данных в среде GRETL 1.7.1……………………………………………. | 19 |
| 1. Цель работы………………………………………………………………………… | 19 |
| 2. Теоретические сведения о линейном регрессионном анализе…………………….. | 19 |
| 3. Описание средств системы Gretl для выполнения регрессионного анализа……………………………………………………………….……………….. | 21 |
| 3.1. Оценка параметров линейной регрессионной модели методом 1МНК (OLS) и проверка адекватности модели……………………………………………………. | 21 |
| 3.2. Анализ выполнения предпосылок 1МНК…….………………………………… | 28 |
| 4. Порядок выполнения лабораторной работы ……………………………………….. | 33 |
| 5. Содержание отчёта о выполнении лабораторной работы…………………………. | 33 |
| Библиографический список…..………………………………………………………. | 34 |
| Приложение А. (справочное) Основные описательные статистики………………. | 35 |
| Приложение Б. (справочное) Статистические таблицы в GRETL…………………. | 36 |
| Приложение В. (справочное) Построение графиков………………………………….. | 38 |
| Лабораторная работа №3. Применение GRETL 1.7.1. при построении и анализе регрессионных моделей с гетероскедастичной случайной составляющей………………………………………………………………………… | 40 |
| 1. Цель работы…………………………………………………………………………… | 40 |
| 2. Теоретические сведения …………………………………………..………………. | 40 |
| 3. Описание средств системы Gretl для выполнения регрессионного анализа при наличии гетероскедастичности……………………………………………………… | 43 |
| 3.1. Пример обнаружения гетероскедастичности в Gretl ………………………….. | 43 |
| 3.2. Оценивание гетероскедастичной модели с использованием взвешенного метода наименьших квадратов ВМНК (WLS)……………………………………… | 50 |
| 4. Порядок выполнения лабораторной работы ……….……………………………. | 59 |
| 5. Содержание отчёта о выполнении лабораторной работы………………………….. | 59 |
| Библиографический список………………………………………………………….. | 60 |
| Лабораторная работа №4. Реализация метода главных компонент в среде GRETL 1.7.1………………………………………………………………………….. | 61 |
| 1. Цель работы………………………………………………………………………… | 61 |
| 2. Теоретический раздел ………………………………………………………………………………. | 61 |
| 3. Пример практической реализации метода главных компонент с использованием системы Gretl………………………………………………….…… | 62 |
| 3.1.3.1. Исходная информация……………………………………………………………. | 63 |
| 3.2.Построение главных компонент и интерпретация результатов моделирования………………………………………………………………………… | 68 |
| 4. Порядок выполнения лабораторной работы ……….……………………………. | 74 |
| 5. Содержание отчёта о выполнении лабораторной работы………………………….. | 76 |
| Библиографический список…..……………………………………………………… | 77 |
| Приложение А. (справочное) Основные показатели результатов деятельности компаний Ford Motor Company и General Motors (2002-2006)……………………… | 78 |
| Лабораторная работа №5. Анализ временных рядов в среде Gretl 1.7.1.……. | 82 |
| 1. Цель работы………………………………………………………………………… | 82 |
| 2. Теоретический раздел ………………………………………….……………………. | 82 |
| 2.1. Анализ тренда………………………………………………………………………. | 83 |
| 2.2. Декомпозиция временного ряда..……………………………………………….. | 85 |
| 2.3. Анализ сезонности. Коррелограмма……………………………………………. | 86 |
| 2.4. Метод авторегрессии……………………………………………………………….. | 87 |
| 2.5. Спектральный (Фурье) анализ…………………………………………………. | 87 |
| 3. Описание средств анализа временных рядов системы Gretl……………………. | 88 |
| 3.1. Пример построение полиномиальной модели тренда…………………………. | 88 |
| 3.2. Пример декомпозиции динамики макроэкономических показателей…………… | 95 |
| 3.3. Пример анализа сезонности с применением коррелограммы ………………… | 102 |
| 3.4. Пример применения метода авторегрессии……………………………………. | 104 |
| 3.5. Пример применения метода спектрального (Фурье) анализа………………… | 107 |
| 4. Порядок выполнения лабораторной работы ……………………………………….. | 109 |
| 5. Содержание отчёта о выполнении лабораторной работы……………………….. | 110 |
| Библиографический список…..……………………………………………………… | 111 |
| Приложение А. (справочное) Исходные данные……………………………………………….. | 112 |
| Лабораторная работа №6 Анализ систем одновременных эконометрических уравнений в среде Gretl 1.7.1………………………………… | 115 |
| 1. Цель работы………………………………………………………………………… | 115 |
| 2. Теоретический раздел…………………………………………..……………………. | 115 |
| 3. Описание средств анализа систем одновременных эконометрических уравнений пакета Gretl………………………………………………….………………… | 117 |
| 4. Порядок выполнения лабораторной работы ……………………………………….. | 128 |
| 5. Содержание отчёта о выполнении лабораторной работы………………………….. | 134 |
| Библиографический список…..……………………………………………………… | 135 |
ЛАБОРАТОРНАЯ РАБОТА №1
ВВЕДЕНИЕ В ПАКЕТ ПРОГРАММ GRETL 1.7.1
Цель работы
Целью данной работы является ознакомление с функциональными возможностями программного продукта Gretl 1.7.1.
ТЕОРЕТИЧЕСКИЙ РАЗДЕЛ
Общие сведения о пакете GRETL
Пакет программ GRETL (GNU Regression Econometrics and Time Series Library) представляет собой инструментарий для практической реализации сложных вычислительных процедур эконометрического моделирования. В 2002 году его автор проф. Аллен Котрелл (США) включил GRETL в проект www.sourceforget.net, делая его общедоступным, бесплатным продуктом с возможностью дальнейшей доработки открытых кодов (Open Source – свободным программным обеспечением). Таким образом, данный пакет программ, статистические данные для обработки, учебное пособие и исходный код всех выпущенных версий доступны на Интернет-сайтах http://gretl.sourceforge.net или http://www.kufel.torun.pl.
Возможности программы:
1. Основные описательные статистики (среднее арифметическое, медиана, минимальное и максимальное значения, среднеквадратическое отклонение, коэффициент изменчивости (вариации), коэффициент асимметрии, коэффициент эксцесса).
2. Проверка нормальности распределения, распределение частот случайной величины, распределение плотности вероятностей, определение коэффициентов корреляции и т.д.
3. Предусматривает непосредственный доступ к статистическим таблицам. Пакет Gretl содержит встроенные статистические таблицы для следующих распределений: нормального, t-распределения Стьюдента, F-распределения Фишера, хи-квадрат, Пуассона, биномиального и распределения Дарбина-Уотсона. Существует возможность вычисления критических значений, p-value.
4. Анализ временных рядов (набор методов оценивания обобщённым МНК, модели ARMAX и GARCH , система уравнений авторегрессии (VAR), проверка коинтеграции; построение линии тренда, коррелограммы, периодограммы; проверка единичных корней, моделирование типа ARIMA, а также процедуры десезонализации X-12-ARIMA и TRAMO).
5. Регрессионный анализ (одношаговый метод наименьших квадратов (1МНК), взвешенный МНК, двухшаговый МНК — оценка систем одновременных уравнений, методы оценивания логитовых, пробитовых и тобитовых моделей и нелинейных моделей, и т.д.)
6. Метод главных компонент.
7. Экспорт и импорт Gretl- Microsoft Excel и текстовые редакторы (Notepad и т.д).
8. Построение графиков и др.
Запуск программы осуществляется через Пуск-Программы-Gretl-Gretl или двойным щелчком мыши по иконке Gretl на рабочем столе.
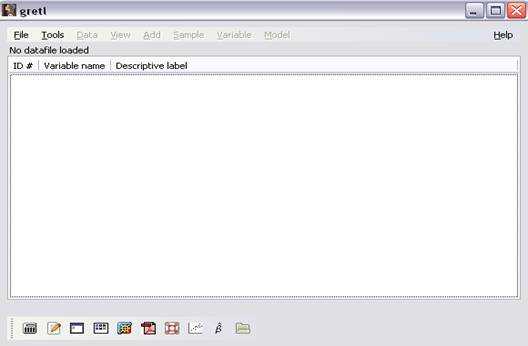
Стартовый экран Gretl
Стартовый экран пакета программ GRETL (рисунок 1) подразделяется на три части:
— Меню, из которого реализуется набор функций.Меню функций состоит из следующих разделов: File(файл), Tools (инструменты), Data(данные),View(вид), Add(добавить), Sample(выборка), Variable (переменная), Model(модель), Help(помощь). Каждый раздел содержит группу программных функций.
— Список переменных (процессов), который содержит перечень названий и описаний переменных открытого набора данных.
— Набор иконок (пронумерованный от 1 до 10), обеспечивает быстрый доступ
к выбранным программным функциям. Набор иконок №1-10, рисунок 1. обеспечивает быстрый доступ к некоторым программным функциям:
1. Открывает окно системного калькулятора.
2. Открывает новое окно для скриптов GRETL.
3. Открывает окно инструкций GRETL.
4. Открывает окно иконок.
5. Обращается к сайту пакета программ GRETL.
6. Открывает окно «Руководство» в pdf формате.
7. Открывает окно помощи.
8. Открывает окно определения графика разброса точек.
9. Открывает окно спецификации модели для оценивания с применением МНК.
10. Открывает окно с примерами – базы фактических данных.
Рисунок 1 — Стартовый экран GRETL
studopedia.net
Пивенко К.А., Баженов Р.И. Построение регрессионной модели в среде Gretl на примере рынка поддержанных автомобилей г. Биробиджана и г. Хабаровска
Пивенко Кристина Александровна1, Баженов Руслан Иванович2
1Приамурский государственный университет им.Шолом-Алейхема, студент
2Приамурский государственный университет им.Шолом-Алейхема, к.п.н., доцент, зав.кафедрой информатики и вычислительной техники
Pivenko Kristina Aleksandrovna1, Bazhenov Ruslan Ivanovich2
1Sholom-Aleichem Priamursky State University, student
2Sholom-Aleichem Priamursky State University, Candidate of pedagogical sciences, associate professor, Head of the Department of Computer Science
Библиографическая ссылка на статью:
Пивенко К.А., Баженов Р.И. Построение регрессионной модели в среде Gretl на примере рынка поддержанных автомобилей г. Биробиджана и г. Хабаровска // Экономика и менеджмент инновационных технологий. 2015. № 4. Ч. 1 [Электронный ресурс]. URL: http://ekonomika.snauka.ru/2015/04/8362 (дата обращения: 07.02.2019).
В современном мире автомобиль перестал быть роскошью, он стал средством передвижения, доступным многим. Для большинства граждан предпочтительнее купить поддержанный автомобиль, а не новый, только что сошедший с конвейера. Какую сумму правильно будет заплатить за б/у автомобиль? За сколько можно продать свой автомобиль? С этими вопросами сталкиваются многие из нас. Чтобы правильно дать ответ, необходимо учесть определенные параметры: тип кузова, год выпуска, объем двигателя, тип коробки передач, пробег. Используя регрессионную модель в среде Gretl, можем найти зависимость стоимости автомобиля от данных параметров.
Ряд ученых изучает проблемы и методы построения различных регрессионных моделей. Базовые принципы использования метода регрессионного анализа были разработаны С.И. Носковым и М.П. Базилевским [1]. Использовалась множественная регрессия О.В. Гусевым и А.В. Жуковым [2] для идентификации перегрузки сервера. А.А. Жарков и Н.А. Анисимова [3] метод множественной регрессии применили для определения рыночной стоимости квартиры с учетом сроков и условий реализации жилья. Расчет логистических издержек при помощи метода множественной регрессии разработан И.А. Семеновым и А.А. Носковым [4]. С использованием Gretl определяются причины трудового оппортунизма сотрудников Р.З. Мухаметзяновым [5]. Особенности использования среды Gretl в целях построения экономических моделей рассматриваются А.А.Тусковым [6]. Особенности применения программных продуктов Excel и Gretl в рамках эконометрического моделирования рассмотрела Ю.Г.Зарезина [7]. Р.И. Баженовым и др. [8-14] изучены проблемы использования регрессионных моделей для анализов различных видов. Изучением регрессионного анализа занимаются также зарубежные ученые [15-16].
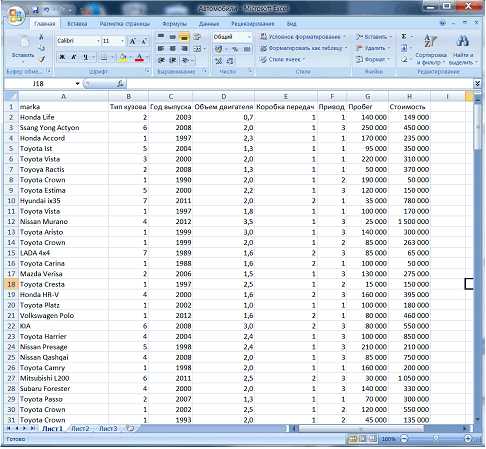
По данным сайта www.avito.ru был осуществлен сбор экспериментальных наблюдений. Рассматривались объявления о продаже автомобилей в г.Биробиджан и в г.Хабаровск. Были выбраны следующие критерии: марка, тип кузова, год выпуска, объем двигателя, тип коробки передач, тип привода, пробег, стоимость.
Тип кузова кодируется следующим образом:
1 – седан;
2 – хэтчбэк;
3 – универсал;
4 – кроссовер;
5 – минивэн;
6 – пикап;
7 – внедорожник;
8 – купе.
Тип коробки передач обозначим:
1 – автоматическая;
2 – механическая.
Привод определим:
1 – передний;
2 – задний;
3 – полный.
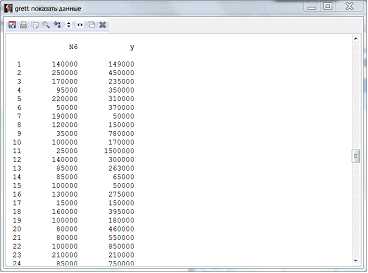
Создадим таблицу данных в MS Excel. Используя данные 200 объявлений (рис.1).
Рисунок 1- Фрагмент данных в Excel
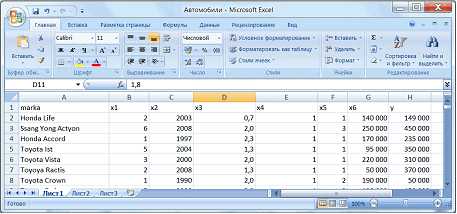
Введем обозначения переменных: тип кузова – х1, год выпуска – х2, объем двигателя – х3, коробка передач – х4, привод – х5, пробег – х6, стоимость – y (рис.2.).
Рисунок 2 – Обозначение переменных
Следующий шаг – открыть данные таблицы Excel в Gretl (рис.3).
Рисунок 3 – Среда Gretl
В окне программы появляются переменные, которые необходимы, чтобы построить регрессионную модель (рис.4).
Рисунок 4 – Рабочее окно программы
Необходимо просмотреть получившуюся таблицу (рис. 5-6).
Рисунок 5 – Контекстное меню выделенных переменных
Рисунок 6 – Просмотр таблицы данных
Так как у нас получилось больше шести столбцов данных, то оставшиеся 2 столбца найдем внизу таблицы (рис.7).
Рисунок 7 – Таблица данных (окончание)
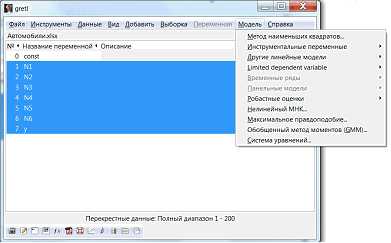
Для решения нашей задачи найдем регрессионную модель, используя метод наименьших квадратов (рис.8).
Рисунок 8 – Меню Модель
Перейдем к построению уравнения модели (рис.9)
Рисунок 9 – Окно спецификации модели
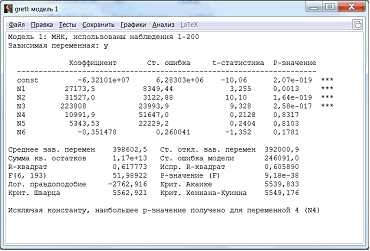
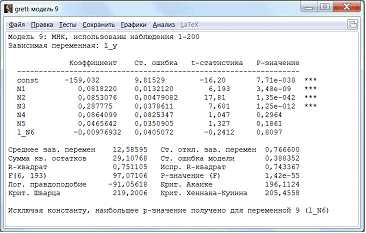
Получившаяся модель и ее описательные статистики показаны на рисунке (рис.10).
Рисунок 10 – Регрессионная модель
По значению R-квадрата можно судить о доле вариации результативного признака с учетом воздействия изучаемых факторов. В данной модели 61,8% вариации переменной Y зависит от влияния включенных факторов, 38,2% обусловлены другими факторами. Если коэффициент выше 80%, то модель считается достаточно хорошей. А у нас слишком низкий R-квадрат. Использование линейной аналитической формы модели может стать вероятной причиной ее слабости. Поэтому найдем другую модель.
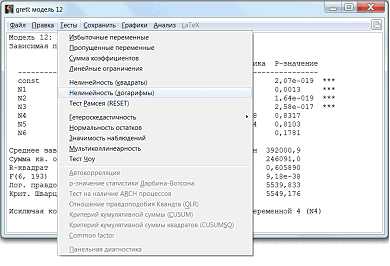
При помощи теста на нелинейность можно проверить обоснованность применения степенной модели (рис.11).
Рисунок 11 – Выбор теста на нелинейность
Проверим модель на нелинейность (логарифмы) (рис. 12).
Рисунок 12 – Тест на нелинейность (логарифмы)
Тест нелинейности для логарифмов (значение p=0,0000001) свидетельствует, что нулевую гипотезу (о линейности аналитической формы) следует отклонить, поскольку значение TR2 = 43,7347 превышает критическое значение х2(1%; 5) = 15,086; по этой причине существуют основания для принятия степенной формы модели (с логарифмированными переменными).
Исследования параметров привели к выводу, что существует логарифмическая зависимость.
Найдем зависимость lny от х1, х2, х3, х4, х5, lnx6 (рис.13).
Рисунок 13 – Новая регрессионная модель
В этой модели R-квадрат у нас уже 75,1%. Значит, модель более точная, чем предыдущая.
Перейдем к решению уравнения
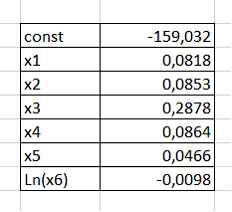
Введем в Excel данные const, х1, х2, х3, х4, х5, х6 (рис. 14). Коэффициенты: a – тип кузова, b – год выпуска, с – объем двигателя, d – коробка передач, e – привод, f – пробег.
Рисунок 14 – Данные в Excel
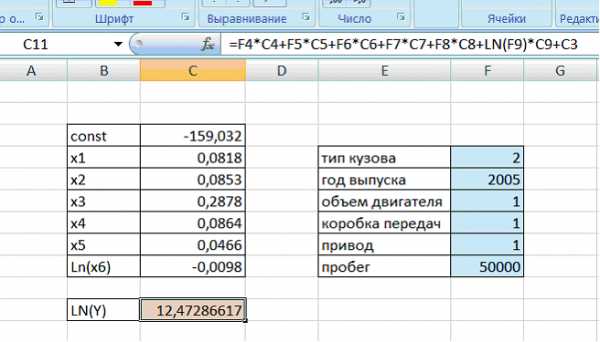
В ячейку, окрашенную в оранжевый цвет, вводим формулу расчета (рис.15). В таблицу Excel вводим необходимые параметры того автомобиля, который мы хотим купить или продать, в ячейки, окрашенные в синий цвет.
Рисунок 15 – Ввод данных
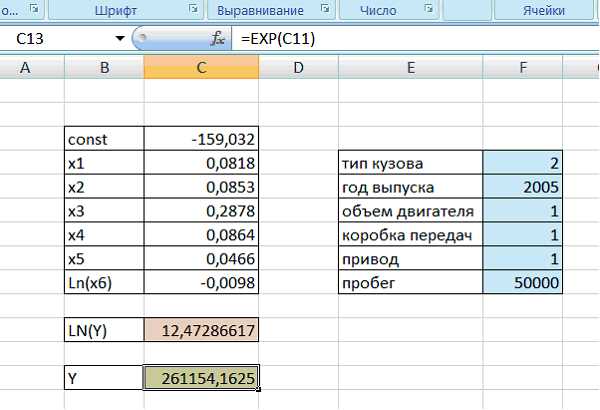
В ячейку, окрашенную в зеленый цвет, вводим формулу расчета стоимости автомобиля. После этого в ячейке, выделенной зеленым цветом, отобразится стоимость данного автомобиля (рис.16).
Рисунок 16 – Расчет стоимости автомобиля по заданным параметрам
Если мы хотим узнать стоимость другого автомобиля, то нужно просто в ячейки, окрашенные в синий цвет ввести другие параметры.
Полученную регрессионную модель можно использовать в работе агентств, занимающихся продажей поддержанных автомобилей. Описание принципов построения регрессионной модели может пригодиться в преподавании студентам различных направлений [17-19].
Библиографический список
- Базилевский М.П., Носков С.И. Методические и инструментальные средства построения некоторых типов регрессионных моделей // Системы. Методы. Технологии. 2012. №1. С. 80-87.
- Гусев О.В., Жуков А.В. Способ идентификации перегрузки с использованием множественной регрессии // Информационная среда вуза XXI века. Материалы VII Международной научно-практической конференции. Петрозаводск, 2013. С. 57-61.
- Жарков А.А., Анисимова Н.А. Механизм формирования стоимости квартир на региональном рынке жилья // Регион: системы, экономика, управление. 2009. № 4. С. 47-53.
- Семенов И.А., Носков А.А. Модель расчета общих логистических издержек методом множественной регрессии // Вестник Саратовского государственного технического университета. 2011. Т. 4. № 2с. С. 397-400.
- Мухаметзянов Р.З. Анализ трудового оппортунизма сотрудников // Science time. 2014. №6 (6). С. 132-147.
- Тусков А.А. Применение Gretl для построения многофакторной модели // Модели, системы, сети в экономике, технике, природе и обществе. 2011. №1. С. 154-159.
- Зарезина Ю.Г. Особенности применения программных продуктов Excel и Gretl в рамках эконометрического моделирования // Новое слово в науке и практике: гипотезы и апробация результатов исследований. 2015. № 15. С. 223-228.
- Пронина О.Ю., Баженов Р.И. Исследование методов регрессионного анализа программной среды Eviews // Nauka-Rastudent.ru. 2015. № 1 (13). С. 45.
- Лагунова А.А., Баженов Р.И. Разработка в среде Gretl регрессионной модели рынка вторичного жилья г. Биробиджана // Nauka-Rastudent.ru. 2015. № 1 (13). С. 40.
- Муллинов Д.О., Баженов Р.И. Разработка в среде Eviews регрессионной модели рынка гаражных помещений г. Биробиджана // Nauka-Rastudent.ru. 2015. № 1 (13). С. 43.
- Баженов Р.И. Информационная безопасность и защита информации: практикум. Биробиджан: Изд-во ГОУВПО «ДВГСГА», 2011. 140 с.
- Vexler V.A., Bazhenov R.I., Bazhenova N.G. Entity-relationship model of adult education in regional extended education system // Asian Social Science. 2014. Т. 10. № 20. С. 1-14.
- Векслер В.А., Баженов Р.И. Формирование модели обучения взрослых основам информационных технологий: региональный аспект: монография. -Биробиджан: Издательский центр ФГБОУ ВПО «ПГУ им. Шолом-Алейхема», 2014. 126 с.
- Наумов А.А., Баженов Р.И. О неустойчивости метода нормализации критериев // Современные научные исследования и инновации. 2014. № 11-1 (43). С. 64-68.
- Baiocchi G., Distaso W. GRETL: Econometric software for the GNU generation // Journal of Applied Econometrics. 2003. Т. 18. №. 1. С. 105-110.
- Mixon Jr J. W., Smith R. J. Teaching undergraduate econometrics with GRETL // Journal of Applied Econometrics. 2006. Т. 21. №. 7. С. 1103-1107.
- Баженов Р.И. Об организации научно-исследовательской практики магистрантов направления «Информационные системы и технологии» // Современные научные исследования и инновации. 2014. № 9-2 (41). С. 62-69.
- Баженов Р.И. Проектирование методики обучения дисциплины «Интеллектуальные системы и технологии» // Современные научные исследования и инновации. 2014. № 5-2 (37). С. 48.
- Баженов Р.И. Об организации деловых игр в курсе «Управление проектами информационных систем» // Научный аспект. 2014. Т. 1. № 1. С. 101-102.
Количество просмотров публикации: Please wait
Все статьи автора «Баженов Руслан Иванович»
ekonomika.snauka.ru
Куфель Т. Эконометрика: решение задач с применением пакета программ GRETL [PDF]
Монография, Варшава, 2007, 200 с.Введение в пакет программ gretl
Лицензия
Инсталляция
Меню и настройки пакета программ gretl
Рабочие сессии и работа с консолью
Статистические данные
Построение набора данных
Ввод данных — импорт данных
Описание набора данных и сохранение файла данных
Объявление типа данных
Агрегирование временных рядов
Преобразование переменных-процессов
Основные описательные статистики
Распределения переменной
Графики
Интернет-сервер со статистическими данными
Примеры из учебных пособий по эконометрике
Статистические тесты
Статистические таблицы в gretl
Калькулятор статистических тестов
Статистические тесты для переменных в базе gretl
Эконометрические модели для срезов данных
Подбор переменных модели — матрица корреляции
Оценивание параметров модели с применением классического метода Наименьших квадратов (кмнк)
Верификация эконометрической модели
Оценивание значимости структурных Параметров, t-тест Стьюдента и f-тест Снедекера.
Оценивание степени соответствия модели
Оценивание нормальности распределения остатков модели
Оценивание однородности дисперсии
Остатков модели. Проверка гетероскедастичности
Оценивание линейности
Аналитической формы модели
Подведение итогов сессии построения
Эконометрической модели
Характеристики экономических процессов
Функции автокорреляции и частичной автокорреляции
Периодограмма и спектр процессов
Проверка единичных корней
Оценивание дробного значения d
Основные модели экономических процессов
Полиномиальные модели тренда — Выбор степени полинома
Эконометрические модели сезонных колебаний
Авторегрессионные модели ar(p)
Модели arma(£ , q)
Модели arima(f , d, q)
Процедуры исключения сезонности
Метод x-12-arima
Метод tramo/seats
Причинно-следственные эконометрические модели экономических процессов
Спецификация модели согласно концепции Конгруэнтного моделирования
Оценивание параметров модели Методом наименьших квадратов
Верификация модели
Исследование значимости оценок
Параметров — исключение a posteriori
Тест автокорреляции дарвина—уотсона
Тест автокорреляции (тест quenouille)
H-тест автокорреляции дарбина
Тест автокорреляции на основании pacf
Тест автокорреляции бройша—годфри
Тест автокорреляции аджунга—бокса
Выявление эффекта arch в процессе остатков
Проверка стабильности Параметров — тест Чоу
Проверка стабильности
Параметров — тест cusum
Проверка нормальности
Распределения остатков
Проверка значимости пропущенных
И добавленных процессов (omit variables, add variables)
Эконометрическое прогнозирование
Прогнозирование по моделям, учитывающим тренд и сезонность
Прогнозы статического и динамического типа
Обобщенный метод наименьших квадратов (омнк)
Оценивание модели в условиях
Автокорреляции случайной составляющей
Метод Кохрейна—Оркотта
Метод Хилдрета—Лу
Метод Прайса—Уинстена
Обобщенный метод Кохрейна—Оркотта
Оценивание модели в условиях гетероскедастичности
Метод корректировки Гетероскедастичности случайной составляющей
Метод HCCM
Взвешенный метод наименьших
Квадратов (случай гетероскедастичности)
Взвешенный метод наименьших квадратов — модели для одноименных наблюдений Специальные модели
Логитовые и пробитовые модели
Тобитовые модели
Системы эконометрических уравнений
Двухшаговый метод наименьших квадратов
модели var
www.twirpx.com
ЭконометрияЛабораторныеGretl — Стр 2
11
2.4.Открытие встроенного или ранее созданного набора данных
ВGRETL существуют встроенные примеры наборов данных (*.gdt),
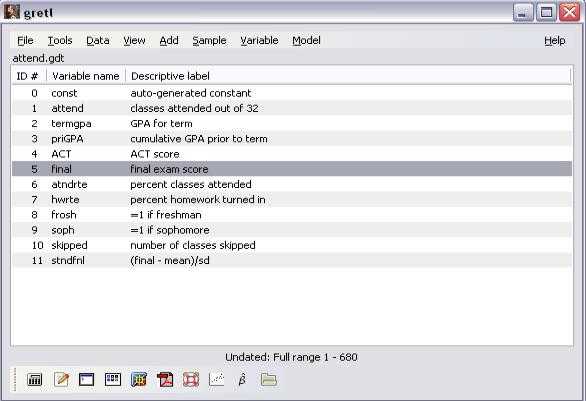
созданные разработчиками и преподавателями. Для их открытия необходимо обратиться к команде FileOpen DataSample File и выбрать (на соответствующей закладке, например Wooldridge) имя открываемого файла, например, attend.gdt двойным щелчком мыши (рисунок 6).
Для просмотра значений отдельной переменной обратимся к команде: VariableDisplay Values (или дважды щёлкнем мышью по названию переменной).
Для просмотра всего набора данных обратимся к команде: ViewIcon
ViewData Set
Открытый набор данных, рисунок 6, состоит из 11 переменных, атрибуты которых -номера(ID#), названия (Variable name) и описанияформулы (Descriptive label)- представлены в списке переменных стартового экрана.
Рисунок 6 — Набор данных Class Attendence Rates and Grades (Посещаемость занятий и оценки) с закладки Wooldridge
Аналогичным образом можно открыть созданные ранее (в Примере 1 и Примере 2) на рабочем столе файлы example1.gdt и example2.gdt при помощи FileOpen DataUser File, выбрав их в открывшемся окне.
Просмотреть общую информацию о наборе данных можно выбрав
DataPrint Description
12
2.5. Редактирование набора статистических данных
Возможны следующие операции над переменными открытого набора данных:
1.Добавление переменной вручную: VariableDefine new variable или из
Excel файла: FileAppend DataExcel
2.Удаление переменной: нажатие кнопки DEL на клавиатуре.
3.Редактирование значений переменной: DataEdit Values.
4.Добавление наблюдений: DataAdd Observations.
5.Изменение атрибутов переменной: VariableEdit Attributes.
6. Просмотр и редактирование всего набора данных:ViewIcon ViewData
Set.
7. Удаление наблюдений с пропущенными значениями: SampleDrop all obs with missing values.
Функция VariableDefine New Variable позволяет добавить ещё одну переменную, а функция DataAdd Observations – добавить определённое число наблюдений к существующему выбранному ряду. Двойной щелчёк мыши по названию переменной позволяет просмотреть ряд её значений, а функция DataEdit Values – редактировать данные значения. Удаление переменной из списка осуществляется нажатием кнопки del на клавиатуре. Чтобы изменить атрибуты переменной необходимо щелчком мыши выбрать её название в списке и вызвать функцию VariableEdit Attributes, затем в открывшемся диалоговом окне ввести новое имя переменной (Name of variable) и её формулу или текстовое описание (Description).
Быстрый доступ к данным функциям возможен из контекстного меню, вызванного нажатием правой кнопкой мыши на выбранной переменной в списке стартового экрана.
Пример 3. Редактирование набора данных example1.gdt: 1. Откроем ранее созданный (Примере1) набор данных example1.gdt:FileOpen DataUser File (рисунок 7)
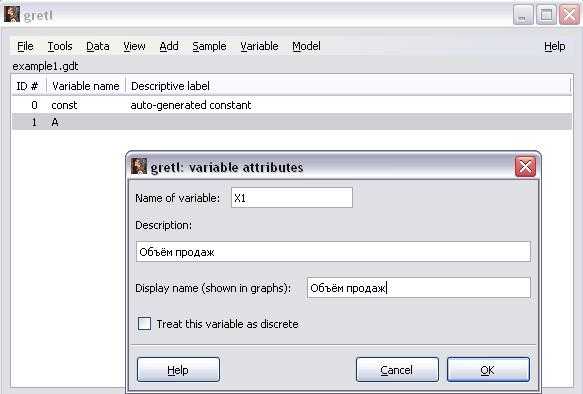
2. Изменим название переменной на X1 и введём её описание «Объём продаж»: VariableEdit Attributes (рисунок 7)
13
Рисунок 7 — Изменение атрибутов переменной: ввод названия и описания
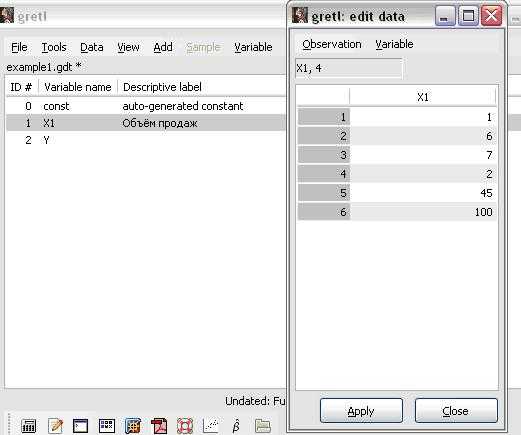
3. Добавим в набор новую переменную Y. Для этого выберем команду Define new variable в менюVariable и в открывшемся окне редактирования введём её значения:
-4,223,8 34,2 748,992 1615 (рисунок 
4.Щелчком мыши выберем переменную X1 из списка (рисунок 
5.В этом же окне «Edit data» вручную изменим значение четвёртого наблюдения на 30,7 (рисунок 8), нажмём кнопки «apply» и «close» для завершения редактирования значений переменной X1.
6.Аналогичным образом выберем переменную Y, обратимся к команде DataEdit Values и введём ещё одно значение ряда 7995.
14
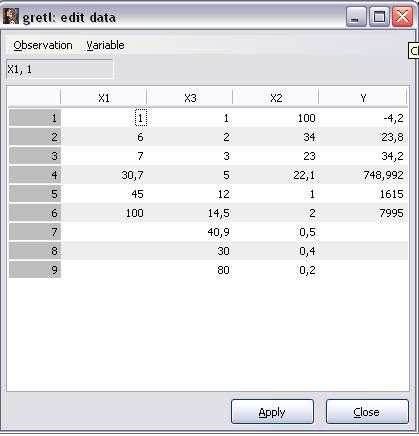
Рисунок 8 — Редактирование значений переменной X1
8.В ранее созданном (в Примере 2.) на рабочем столе файле example2.xls изменим название переменной X1 на X3. Затем добавим к редактируемому в данном примере набору данных example1.gdt переменные из файла example2.xls: FileAppend DataExcel (выбрать название файла). В результате в список переменных стартового экрана будут добавлены переменные X2 и X3.
9.Откроем весь набор данных для редактирования: ViewIcon ViewData Set (рисунок 9).
10.Удалим наблюдения №7-9с пропущенными значениями переменных X1 и Y, сократив выборку до шести первых наблюдений:SampleDrop all obs with missing values. Нажмём кнопки «apply» и «close». Сохраним набор данныхFileSave Data, ответив «no» на вопрос о восстановлении первоначального размера выборки.
15
Рисунок 9 — Окно редактирования набора данных
2.6. Экспорт данных
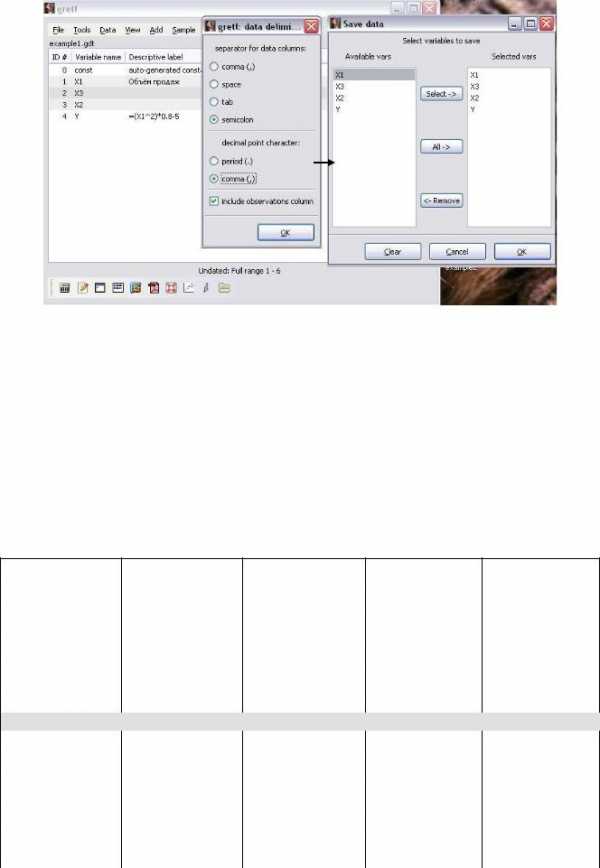
Экспорт данных в Excel осуществляется с использование команды FileExport DataSCV Экспортируем в Excel полученный в Примере 3 набор данных:
1.Откроем в Gretl файл example1.gdt (FileOpen DataUser File).
2.Обратимся к команде FileExport DataSCV. В открывшемся окне поставим флажки разделителей semicolon и comma (,) для интерпретации информации в Excel как количественных данных в отдельных столбцах, рисунок 10.
3.В открывшемся окне Save Data при помощи кнопки Select перенесём все переменные из списка в левой части окна в правую часть и нажмём кнопку ОК.
4.Введём имя файла example1.csv и нажмём кнопку save. Данный файл появится на рабочем столе.
16
Рисунок 10 — Экспорт данных из среды GRETL в таблицу Excel
3.ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
1.Выполнить примеры №1-3данных методических указаний.
2.Выполнить упражнения №1-3согласно варианту.
3.Подготовить отчёт по выполненной работе в электронном виде (MS-Word).Упражнение 1. Создать набор данных из двух переменных X1 и X2(тип
данных – cross-sectional)по исходной информации, представленной в таблице 4 согласно варианту. Сохранить в файл Ex1.gdt на рабочем столе и закрыть созданный набор данных.
Таблица 4 -Значенияпеременной X1 и X2 по вариантам№№1-10
|
№1 |
№2 |
№3 |
№4 |
№5 |
|||||
|
3 |
1 |
3,5 |
2 |
3,6 |
1 |
10 |
11 |
0 |
10 |
|
5,3 |
5,3 |
5,3 |
5,3 |
5,3 |
5,3 |
5,3 |
5,3 |
5,3 |
6,3 |
|
7 |
7 |
9 |
7,5 |
7,1 |
7 |
7,9 |
41,5 |
7,1 |
7 |
|
10,3 |
10,3 |
10,3 |
10,3 |
10,3 |
10,3 |
10,3 |
10,3 |
10,3 |
10,3 |
|
40,2 |
40 |
30,2 |
40,2 |
30,2 |
40,2 |
40,2 |
40,2 |
40,2 |
40,2 |
|
80 |
80 |
80 |
80 |
80 |
81 |
80 |
80 |
80 |
87 |
|
100 |
101 |
200 |
100 |
100 |
101 |
100 |
100 |
100 |
106 |
|
120 |
120 |
130 |
120 |
129 |
121 |
120 |
128 |
120 |
125 |
|
№6 |
№7 |
№8 |
№9 |
№10 |
|||||
|
3 |
1 |
3,5 |
2 |
3,6 |
1 |
10 |
11 |
0 |
10 |
|
5,3 |
5,3 |
5,3 |
5,3 |
5,3 |
5,3 |
5,3 |
5,3 |
5,3 |
6,3 |
|
7 |
7 |
9 |
7,5 |
7,1 |
7 |
7,9 |
41,5 |
7,1 |
7 |
|
10,3 |
10,3 |
10,3 |
10,3 |
10,3 |
10,3 |
10,3 |
10,3 |
10,3 |
10,3 |
|
40,2 |
40 |
30,2 |
40,2 |
30,2 |
40,2 |
40,2 |
40,2 |
40,2 |
40,2 |
|
80 |
80 |
80 |
80 |
80 |
81 |
80 |
80 |
80 |
87 |
|
100 |
101 |
200 |
100 |
100 |
101 |
100 |
100 |
100 |
106 |
|
120 |
120 |
130 |
120 |
129 |
121 |
120 |
128 |
120 |
125 |
17
Упражнение 2.
Импортировать файл example2.xls (созданный в вышеописанном Примере 2) в среду Gretl как временной ряд с поквартальными данными, начиная с даты X.0X.2008г., где Х – номер варианта.
Упражнение 3.
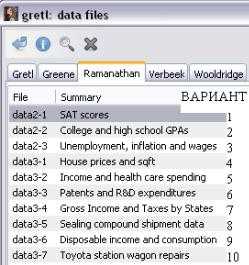
1.Открыть встроенный набор данных FileOpen dataSample FileRamanathanфайл в зависимости от варианта (рисунок 11).
2.Просмотреть общую текстовую информацию о наборе данных
DataPrint Description.
3.Изменить первые три значения одной из переменных.
4.Сократить выборку на последние пять наблюдений.
5.Экспортировать данные в таблицу Excel.
Рисунок 11 — Варианты заданий для выполнения упражнения 3
4. СОДЕРЖАНИЕ ОТЧЕТА О ВЫПОЛНЕНИИ ЛАБОРАТОРНОЙ РАБОТЫ
1)Название и цель работы.
2)Постановка задачи.
3)Этапы выполнения задачи в Gretl.
4)Выводы.
18
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1.Куфель Т. Эконометрика. Решение задач с применением пакета программ GRETL / Т. Куфель. — М.: Горячая линия – Телеком, 2007. – 200с.
2.Using gretl for Principles of Econometrics, 3rd Edition Version 1.01 Lee C. Adkins Professor of Economics Oklahoma State University // http://www.learneconometrics.com/gretl.html
3.Уокенбах Дж. Microsoft Office Excel 2007. Библия пользователя / Дж. Уокенбах. — М.: Диалектика, 2008.- 816с.
4.Карлберг К. Бизнес-анализс помощью Microsoft Excel/ К. Карлберг — М.: Вильямс, 2007.- 464с.
5.Джелен Б. Сводные таблицы в Microsoft Excel/ Б. Джелен — М.: Вильямс, 2007.- 320с.
19
ЛАБОРАТОРНАЯ РАБОТА №2 ЛИНЕЙНЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ ВЗАИМОСВЯЗИ
СТАТИСТИЧЕСКИХ ДАННЫХ В СРЕДЕ GRETL 1.7.1.
1. ЦЕЛЬ РАБОТЫ
Целью данной работы является получение практических навыков регрессионного анализа в системе Gretl для автоматизированного поиска ранее неизвестных закономерностей в имеющихся в распоряжении менеджера данных с последующим использованием полученной информации для подготовки управленческих решений.
2. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ О ЛИНЕЙНОМ РЕГРЕССИОННОМ АНАЛИЗЕ
|
Целью |
регрессионного |
анализа является оценка функциональной |
|
|
зависимости |
ˆ |
…, xn ) |
u результативного признака (y) от факторных |
|
y f (x1, x2, |
(x1, x2, …, xn ) . Формулы (1) и (2) представляют собой линейные модели парной и множественной регрессии соответственно.
|
y f (x) u0 1 x u, |
(1) |
|
y 0 1 x1 n xn u, |
(2) |
где y — фактическое значение результативного признака;xi -признак-фактор;
ai – параметр регрессионной модели;
u — случайная ошибка (остаток), характеризующая отклонения реального значения результативного признака от теоретического. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения.
Оценивание параметров линейной модели основан на обычном или одношаговом методе наименьших квадратов (1МНК или OLS – Ordinary Least Squares).
Этот метод позволяет получить такие оценки параметров, при которых
сумма квадратов отклонений фактических значений результативного признака
~
(y) от расчетных (теоретических)yx минимальна, формула (3).
|
~ |
2 |
min , |
(3) |
||||||
|
( yiyxi |
) |
||||||||
|
i |
|||||||||
|
Статистическое |
моделирование |
связи |
методом |
линейного |
|||||
|
регрессионного анализа осуществляется в 3 этапа: |
|||||||||
|
a) Оценка |
параметров линейной |
регрессионной |
модели методом |
||||||
|
1МНК |
|||||||||
|
Вектор оценок |
параметров модели |
(2) определяется |
выражением (4). |
||||||
|
1 |
X T Y |
(4) |
|||||||
|
X T X |
|||||||||
|
b) Проверка |
адекватности регрессионной |
модели |
(проверки |
значимости индивидуальных оценок коэффициентов модели с помощью t-
20
критерия Стьюдента и оценка значимости уравнения регрессии в целом с помощью F-критерияФишера)
На первом шаге проверки адекватности (качества) модели оценивается существенность влияния каждой объясняющей переменной xi , на зависимую переменную y, для этого необходимо оценить значимость полученных параметров i , используя t- критерий Стьюдента, формула (5). Значимость
параметра определяется путём проверки нулевой гипотезы о равенстве его нулю (для выбранного уровня значимости).
|
t p |
i |
, |
(5) |
||||||
|
2 |
|||||||||
|
i |
|||||||||
|
i |
|||||||||
|
где i — оценкаi -гокоэффициента модели, COEFFICIENT; |
|||||||||
|
2 |
— оценка дисперсии параметра |
, |
2 = STDERROR. |
||||||
|
i |
i |
i |
На втором шаге проверки адекватности модели оценивается её значимость (пригодность) в целом , используя показатели: F-критерий Фишера, формула (6), коэффициент детерминации R 2 , формула (7), (Unadjusted R2 и Adjusted R2), сумма квадратов остатков RSS Sum of squared residuals),
стандартная ошибка регрессии (Standard error of residuals), информационные критерии (Akaike information criterion, Schwarz Bayesian criterion, Hannan-Quinncriterion).
Значимость регрессии проверяется путём проверки нулевой гипотезы о равенстве нулю всех параметров модели (для выбранного уровня значимости).
|
Fр |
R2 |
n k |
, |
(6) |
|||
|
R2 |
k 1 |
||||||
|
1 |
где R 2 — коэффициент детерминации — часть вариации (дисперсии) зависимой переменной y, которая объясняется уравнением регрессии, UNADJUSTED R2.
|
R2 |
ˆ Т XТ Y n Y |
2 |
, |
(7) |
||||
|
Y Т Y n Y2 |
||||||||
n — число наблюдений;
k – число коэффициентов факторов.
При анализе адекватности уравнения регрессии исследуемому процессу возможны следующие варианты:
— Построенная модель на основе ее проверки по F-критериюФишера в целом адекватна, и все коэффициенты регрессии значимы. Такая модель может
быть использована для принятия решений к осуществлению прогнозов.
— Модель по F-критериюФишера адекватна, но часть коэффициентов регрессии незначима. В этом случае модель пригодна для принятия
некоторых решений, но не для производства прогнозов.
— Модель по F-критериюФишера адекватна, но все коэффициенты регрессии
studfiles.net
Куфель Т. Эконометрика: решение задач с применением пакета программ GRETL — Материалы по Gretl — Специальная литература — Каталог материалов
Рассмотрены методы решения основных эконометрических задач с использованием пакета программ GRETL (GNU Regression Econometrics Time-series Library), предназначенного для практической реализации сложных вычислительных процедур эконометрического моделирования. Пакет программ GRETL и представленные в работе статистические данные доступны на интернет-сайте автора http://www.kufel.torun.pl. Для студентов, аспирантов и преподавателей экономических ВУЗов, а также для научных работников, ведущих экономические исследования.
СОДЕРЖАНИЕ
Предисловие к русскому изданию
Предисловие
1. Введение в пакет программ GRETL
1.1. Лицензия
1.2. Инсталляция
1.3. Меню и настройки пакета программ GRETL
1.4. Рабочие сессии и работа с консолью
2. Статистические данные
2.1. Построение набора данных
2.2. Ввод данных — импорт данных
2.3. Описание набора данных и сохранение файла данных
2.4. Объявление типа данных
2.5. Агрегирование временных рядов
2.6. Преобразование переменных-процессов
2.7. Основные описательные статистики
2.8. Распределения переменной
2.9. Графики
2.10. Интернет-сервер со статистическими данными
2.11. Примеры из учебных пособий по эконометрике
3. Статистические тесты
3.1. Статистические таблицы в GRETL
3.2. Калькулятор статистических тестов
3.3. Статистические тесты для переменных в базе GRETL
4. Эконометрические модели для срезов данных
4.1. Подбор переменных модели — матрица корреляции
4.2. Оценивание параметров модели с применением классического метода наименьших квадратов (КМНК)
4.3. Верификация эконометрической модели
4.3.1. Оценивание значимости структурных Параметров, t-тест Стьюдента и F-тест Снедекера.
4.3.2. Оценивание степени соответствия модели
4.3.3. Оценивание нормальности распределения остатков модели
4.3.4. Оценивание однородности дисперсии остатков модели. Проверка гетероскедастичности
4.3.5. Оценивание линейности аналитической формы модели
4.4. Подведение итогов сессии построения эконометрической модели
5. Характеристики экономических процессов
5.1. Функции автокорреляции и частичной автокорреляции
5.2. Периодограмма и спектр процессов
5.3. Проверка единичных корней
5.4. Оценивание дробного значения d
6. Основные модели экономических процессов
6.1. Полиномиальные модели тренда — Выбор степени полинома
6.2. Эконометрические модели сезонных колебаний
6.3. Авторегрессионные модели AR(p)
6.4. Модели ARMA(£ , q)
6.5. Модели ARIMA(f , d, q)
6.6. Процедуры исключения сезонности
6.6.1. Метод X-12-ARIMA
6.6.2. Метод TRAMO/SEATS
7. Причинно-следственные эконометрические модели экономических процессов
7.1. Спецификация модели согласно концепции Конгруэнтного моделирования
7.2. Оценивание параметров модели Методом наименьших квадратов
7.3. Верификация модели
7.3.1. Исследование значимости оценок параметров — исключение a posteriori
7.3.2. Тест автокорреляции Дарвина—Уотсона
7.3.3. Тест автокорреляции (тест Quenouille)
7.3.4. H-тест автокорреляции Дарбина
7.3.5. Тест автокорреляции на основании PACF
7.3.6. Тест автокорреляции Бройша—Годфри
7.3.7. Тест автокорреляции Аджунга—Бокса
7.3.8. Выявление эффекта ARCH в процессе остатков
7.3.9. Проверка стабильности параметров — тест Чоу
7.3.10. Проверка стабильности параметров — тест CUSUM
7.3.11. Проверка нормальности распределения остатков
7.3.12. Проверка значимости пропущенных и добавленных процессов (omit variables, add variables)
8. Эконометрическое прогнозирование
8.1. Прогнозирование по моделям, учитывающим тренд и сезонность
8.2. Прогнозы статического и динамического типа
9. Обобщенный метод наименьших квадратов (омнк)
9.1. Оценивание модели в условиях автокорреляции случайной составляющей
9.1.1. Метод Кохрейна—Оркотта
9.1.2. Метод Хилдрета—Лу
9.1.3. Метод Прайса—Уинстена
9.1.4. Обобщенный метод Кохрейна—Оркотта
9.2. Оценивание модели в условиях гетероскедастичности
9.2.1. Метод корректировки Гетероскедастичности случайной составляющей
9.2.2. Метод HCCM
9.2.3. Взвешенный метод наименьших квадратов (случай гетероскедастичности)
9.3. Взвешенный метод наименьших квадратов — модели для одноименных наблюдений
10. Специальные модели
10.1. Логитовые и пробитовые модели
10.1.1. Прогнозирование двоичной переменной
10.2. Тобитовые модели
11. Системы эконометрических уравнений
11.1. Двухшаговый метод наименьших квадратов
11.2. Модели VAR
11.2.1. Проверка значимости временного лага порядка p
11.2.2. Функция импульсных откликов в модели VAR
Литература
www.statproject.ru
А. С. Малова
Основы эконометрики в среде GRETL
Учебное пособие
[email protected]
Введение
Цель данного пособия – познакомить читателя с основами проведения эконометрических исследований в среде GRETL. Основная аудитория данной книги – студенты бакалавриата, обучающиеся по направлениям «Экономика», «Бизнес-информатика», «Управление персоналом», «Менеджмент», однако она может быть полезна и студентам других направлений, а также представителям бизнес-сообщества, которые по роду своей деятельности столкнулись с необходимостью проведения эконометрических исследований. Данное учебное пособие – это попытка практического изложения основ эконометрики с минимальными теоретическими выкладками, при этом предполагается, что недостаток теоретических знаний должен быть восполнен читателем самостоятельно с помощью учебников по основам эконометрики. Для обеспечения связи практических навыков с теоретическими знаниями в области эконометрики ко всем рассматриваемым темам даются ссылки на литературу. При этом основная задача данного пособия – помочь читателю в освоении эконометрики, изложить некоторые технические аспекты проведения исследований с использованием среды GRETL. Почему именно GRETL? Данный эконометрический пакет является бесплатным программным продуктом, который, с одной стороны, доступен любому пользователю, а с другой – обладает достаточно обширными возможностями для анализа данных и проведения эмпирических исследований. Немаловажным является и то, что в GRETL имеется значительный пул данных из большинства классических зарубежных учебников по основам эконометрики, что позволит достаточно легко переключиться с простейших примеров, рассмотренных в данном пособии, на более сложные содержательные задачи и кейсы из учебников.
В данном пособии весь материал излагается с точки зрения практики – то есть все основные разделы курса эконометрики для бакалавриантов даны в примерах и задачах. Поскольку невозможно приобрести навык проведения эконометрических расчетов, только изучая учебник, предполагается, что читатель должен иметь возможность проделать все излагаемые действия на практике. С этой целью в пособии использовались данные из учебника J. M. Wooldridge «Basic econometrics», которые доступны в GRETL. Все наборы данных при первом обращении к ним в пособии обозначены ссылками и указателями на источник.
Перед тем как начать осваивать основы эконометрики в среде GRETL, необходимо скачать и установить на свой компьютер сам статистический пакет. Он доступен по ссылке http://GRETL.sourceforge.net/. Вся информация о том, как установить GRETL, приводится на сайте, поэтому нет нужды в подробном изложении, стоит лишь сказать, что программа имеет версию как под ОС Windows, так и под Mac OS, а также что библиотеки данных должны быть установлены отдельно, для этого нужно перейти по ссылке http://GRETL.sourceforge.net/GRETL_data.html.
Удачи в проведении интересных, содержательных и полезных эконометрических исследований!
1. Линейная регрессионная модель
Для начала введем некоторые обозначения. Предположим, что некоторая величина Y зависит от величин . Введем понятие регрессионного уравнения – это уравнение вида , где . Через n обозначим число наблюдений, по которым строится регрессия, k – число регрессоров в модели, – случайная величина, которая носит название ошибки регрессии.
Модель такого вида называется классической линейной регрессионной моделью (ЛРМ) в случае, если выполняются следующие предпосылки:
1. , – линейная спецификация модели, где – коэффициенты модели, которые подлежат определению, , – ошибки модели.
2. , – детерминированные величины.
3. – математическое ожидание ошибок равно нулю, , дисперсия ошибок не зависит от номера наблюдения.
4. , – совместное математическое ожидание ошибок разных наблюдений равно нулю.
5. Если выполняется дополнительная предпосылка о нормальном распределении ошибок , то классическая линейная регрессионная модель называется нормальной линейной регрессионной моделью (НЛРМ).
Подробнее о предпосылках линейной регрессионной модели можно прочесть в [2, 3].
2. Оценка линейной регрессионной модели
Рассмотрим множественную линейную регрессию
, ,
где – средний уровень заработной платы в час в долларах, – образование в годах, – общий стаж работы в годах, – опыт работы у текущего работодателя, в годах, – ошибка регрессии, n – число наблюдений [файл с данными wage1.gdt].
Для того чтобы оценить предложенную модель по методу наименьших квадратов (МНК), используем команду меню Модель – Метод наименьших квадратов.
В появившемся диалоговом окне в поле Зависимая переменная помещаем переменную (для этого выделяем ее курсором в списке переменных и нажимаем на стрелку, соответствующую окну Зависимая переменная. Данный способ перемещения переменных справедлив для всех операций с диалоговыми окнами).
Для дальнейшего удобства можно поставить галочку в окошке Установить по умолчанию. Это делается для того, чтобы при изменении спецификации исследуемой модели зависимая переменная не менялась. В окно Регрессоры отправляем регрессоры модели – это переменные , , .
Рис. 2.1
После этого нажимаем ОК. В результате коэффициенты модели были оценены методом наименьших квадратов. Результат оценки представлен на рис. 2.2.
Рис. 2.2
Для того чтобы понимать, какие результаты позволяет получить GRETL, разберем информацию, представленную на распечатке по строкам сверху вниз.
В первой строке указывается метод оценки и количество наблюдений, по которым производилась оценка. Достаточно часто случается, что количество наблюдений, по которым производилась оценка, не совпадает с числом наблюдений в исходной выборке, даже если она не была ограничена. Это может быть связано, например, с наличием пропусков в данных.
Вторая строка напоминает нам о том, какая переменная была выбрана в качестве зависимой.
После двух первых строк следуют подтаблицы непосредственно с результатами оценивания. В первой подтаблице указаны регрессоры, включенные в модель, напротив каждого из них указывается его коэффициент (столбец Коэффициенты), стандартная ошибка оценки коэффициента (столбец Ст. ошибка), значение статистики Стьюдента для коэффициента (столбец t-статистика) и вероятность ошибки I рода (столбец P-значение). Стоит отметить, что константа тоже является регрессором, и для нее также рассчитываются все указанные характеристики.
По распечатке, представленной на рис. 2.2, мы можем выписать получившееся уравнение регрессии:
Аналогично можно получить оцененное уравнение и в GRETL, для этого выбираем в меню регрессии Файл – Просмотреть как уравнение.
Рис. 2.3
Однако для того, чтобы иметь возможность дать интерпретацию коэффициентам регрессии и строить прогнозы, необходимо проверить, является ли полученная модель адекватной.
Для этого, в свою очередь, необходимо провести ряд эконометрических тестов, а именно проверить значимость регрессии в целом, значимость отдельных коэффициентов регрессии, оценить качество полученного регрессионного уравнения. Вообще говоря, перед проверкой значимости и качества уравнения необходимо провести тесты на выполнение основных предпосылок линейной регрессионной модели (гомоскедастичность, отсутствие автокорреляции). На данном этапе мы будем считать эти тесты проведенными и вернемся к вопросам выполнения предпосылок ЛРМ позднее.
3. Тест Фишера (Fisher test)
Для начала проверим гипотезу о незначимости регрессии в целом. Тест позволит понять, является ли построенная модель адекватной с точки зрения статистики. Для этой цели воспользуемся тестом Фишера [3].
Сформулируем гипотезы для проверки незначимости регрессии в целом в рассматриваемом примере [файл с данными wage1.gdt] модели , :
как минимум один из коэффициентов отличен от нуля.
Уважаемый посетитель, Вы зашли на сайт как незарегистрированный пользователь.
Мы рекомендуем Вам зарегистрироваться либо войти на сайт под своим именем.
А. С. Малова
Основы эконометрики в среде GRETL Учебное пособие
Москва 2016
УДК 330.115(075.8) ББК 65.в6я73 М18
Электронные версии книг на сайте www.prospekt.org
Автор: Малова А. С. — кандидат экономических наук, старший преподаватель кафедры экономической кибернетики СПбГУ, приглашенный преподаватель СПбГЭУ (программы второго высшего образования, президентская программа, Master of International Business Administration). Преподает эконометрику, статистический анализ бизнес-информации, статистические методы в менеджменте. Рецензент: Подкорытова О. А. — кандидат физико-математических наук, доцент кафедры экономической кибернетики СПбГУ.
М18
Малова А. С. Основы эконометрики в среде GRETL : учебное пособие. — Москва : Проспект, 2016. — 112 с. ISBN 978-5-392-20334-5 Данное пособие представляет собой вспомогательный методический материал для работы в эконометрической среде GRETL. Оно предназначено студентам бакалавриата по направлениям «Экономика», «Бизнес-информатика», «Управление персоналом», «Менеджмент» для использования на практических и семинарских занятиях по курсу «Эконометрика (пространственные данные)», а также может использоваться любыми заинтересованными лицами в качестве краткого руководства по использованию GRETL. Пособие включает в себя обзор основных тем базового курса «Эконометрика», подробный разбор возможностей и функций эконометрического пакета GRETL, а также примеры практической реализации тех или иных методов. В данном издании для иллюстрации возможностей эконометрического пакета использовались примеры из учебника Jeffrey M. Wooldridge «Introductory Econometrics: A Modern Approach, 2nd edition». Все файлы с данными находятся в открытом доступе и могут быть свободно использованы. Пособие организовано таким образом, что читатель имеет возможность самостоятельно проделать все действия, необходимые для решения стоящей перед ним эконометрической задачи.
УДК 330.115(075.8) ББК 65.в6я73 Учебное издание
Малова Александра Сергеевна ОСНОВЫ ЭКОНОМЕТРИКИ В СРЕДЕ GRETL Учебное пособие Оригинал-макет подготовлен компанией ООО «Оригинал-макет» www.o-maket.ru; тел.: (495) 726-18-84 Санитарно-эпидемиологическое заключение № 77.99.60.953.Д.004173.04.09 от 17.04.2009 г. Подписано в печать 20.01.2016. Формат 60×901/16. Печать цифровая. Печ. л. 7,0. Тираж 1000 (1-й завод 50) экз. Заказ № ООО «Проспект» 111020, г. Москва, ул. Боровая, д. 7, стр. 4.
ISBN 978-5-392-20334-5
© Малова А. С., 2016 © ООО «Проспект», 2016
ВВЕДЕНИЕ Цель данного пособия — познакомить читателя с основами проведения эконометрических исследований в среде GRETL. Основная аудитория данной книги — студенты бакалавриата, обучающиеся по направлениям «Экономика», «Бизнес-информатика», «Управление персоналом», «Менеджмент», однако она может быть полезна и студентам других направлений, а также представителям бизнессообщества, которые по роду своей деятельности столкнулись с необходимостью проведения эконометрических исследований. Данное учебное пособие — это попытка практического изложения основ эконометрики с минимальными теоретическими выкладками, при этом предполагается, что недостаток теоретических знаний должен быть восполнен читателем самостоятельно с помощью учебников по основам эконометрики. Для обеспечения связи практических навыков с теоретическими знаниями в области эконометрики ко всем рассматриваемым темам даются ссылки на литературу. При этом основная задача данного пособия — помочь читателю в освоении эконометрики, изложить некоторые технические аспекты проведения исследований с использованием среды GRETL. Почему именно GRETL? Данный эконометрический пакет является бесплатным программным продуктом, который, с одной стороны, доступен любому пользователю, а с другой — обладает достаточно обширными возможностями для анализа данных и проведения эмпирических исследований. Немаловажным является и то, что в GRETL имеется значительный пул данных из большинства классических зарубежных учебников по основам эконометрики, что позволит достаточно легко переключиться с простейших примеров, рассмотренных в данном пособии, на более сложные содержательные задачи и кейсы из учебников. В данном пособии весь материал излагается с точки зрения практики — то есть все основные разделы курса эконометрики для бакалавриантов даны в примерах и задачах. Поскольку невозможно приобрести навык проведения эконометрических расчетов, только изучая учебник, предполагается, что читатель должен иметь возможность проделать все излагаемые действия на практике. С этой целью в пособии использовались данные из учебника J. M. Wooldridge «Basic econometrics», которые доступны в GRETL. Все наборы данных при
4
•
А. С. Малова. Основы эконометрики в среде GRETL
первом обращении к ним в пособии обозначены ссылками и указателями на источник. Перед тем как начать осваивать основы эконометрики в среде GRETL, необходимо скачать и установить на свой компьютер сам статистический пакет. Он доступен по ссылке http://GRETL.sourceforge.net/. Вся информация о том, как установить GRETL, приводится на сайте, поэтому нет нужды в подробном изложении, стоит лишь сказать, что программа имеет версию как под ОС Windows, так и под Mac OS, а также что библиотеки данных должны быть установлены отдельно, для этого нужно перейти по ссылке http://GRETL.sourceforge.net/GRETL_data.html. Удачи в проведении интересных, содержательных и полезных эконометрических исследований!
1. ЛИНЕЙНАЯ РЕГРЕССИОННАЯ МОДЕЛЬ Для начала введем некоторые обозначения. Предположим, что некоторая величина Y зависит от величин . Введем понятие регрессионного уравнения — это уравнение вида , где . Через n обозначим число наблюдений, по которым строится регрессия, k — число регрессоров в модели, — случайная величина, которая носит название ошибки регрессии. Модель такого вида называется классической линейной регрессионной моделью (ЛРМ) в случае, если выполняются следующие предпосылки: 1. , — линейная спецификация модели, где — коэффициенты модели, которые подлежат определению, , — ошибки модели. 2. , — детерминированные величины. 3.
— математическое ожидание ошибок равно нулю, , дисперсия ошибок не зависит от номера наблюдения.
4.
, — совместное математическое ожидание ошибок разных наблюдений равно нулю. 5. Если выполняется дополнительная предпосылка о нормальном распределении ошибок , то классическая линейная регрессионная модель называется нормальной линейной регрессионной моделью (НЛРМ). Подробнее о предпосылках линейной регрессионной модели можно прочесть в [2, 3].
2. ОЦЕНКА ЛИНЕЙНОЙ РЕГРЕССИОННОЙ МОДЕЛИ Рассмотрим множественную линейную регрессию , , где — средний уровень заработной платы в час в долларах, — образование в годах, — общий стаж работы в годах, — опыт работы у текущего работодателя, в годах, — ошибка регрессии, n — число наблюдений [файл с данными wage1.gdt]. Для того чтобы оценить предложенную модель по методу наименьших квадратов (МНК), используем команду меню Модель — Метод наименьших квадратов. В появившемся диалоговом окне в поле Зависимая переменная помещаем переменную (для этого выделяем ее курсором в списке переменных и нажимаем на стрелку, соответствующую окну Зависимая переменная. Данный способ перемещения переменных справедлив для всех операций с диалоговыми окнами). Для дальнейшего удобства можно поставить галочку в окошке Установить по умолчанию. Это делается для того, чтобы при изменении спецификации исследуемой модели зависимая переменная не менялась. В окно Регрессоры отправляем регрессоры модели — это переменные , , .
Рис. 2.1
• 7
2. Оценка линейной регрессионной модели
После этого нажимаем ОК. В результате коэффициенты модели были оценены методом наименьших квадратов. Результат оценки представлен на рис. 2.2.
Рис. 2.2
Для того чтобы понимать, какие результаты позволяет получить GRETL, разберем информацию, представленную на распечатке по строкам сверху вниз. В первой строке указывается метод оценки и количество наблюдений, по которым производилась оценка. Достаточно часто случается, что количество наблюдений, по которым производилась оценка, не совпадает с числом наблюдений в исходной выборке, даже если она не была ограничена. Это может быть связано, например, с наличием пропусков в данных. Вторая строка напоминает нам о том, какая переменная была выбрана в качестве зависимой. После двух первых строк следуют подтаблицы непосредственно с результатами оценивания. В первой подтаблице указаны регрессоры, включенные в модель, напротив каждого из них указывается его коэффициент (столбец Коэффициенты), стандартная ошибка оценки коэффициента (столбец Ст. ошибка), значение статистики Стьюдента для коэффициента (столбец t-статистика) и вероятность ошибки I рода (столбец P-значение). Стоит отметить, что константа тоже является регрессором, и для нее также рассчитываются все указанные характеристики. По распечатке, представленной на рис. 2.2, мы можем выписать получившееся уравнение регрессии: . Аналогично можно получить оцененное уравнение и в GRETL, для этого выбираем в меню регрессии Файл — Просмотреть как уравнение.
8
•
А. С. Малова. Основы эконометрики в среде GRETL
Рис. 2.3
Однако для того, чтобы иметь возможность дать интерпретацию коэффициентам регрессии и строить прогнозы, необходимо проверить, является ли полученная модель адекватной. Для этого, в свою очередь, необходимо провести ряд эконометрических тестов, а именно проверить значимость регрессии в целом, значимость отдельных коэффициентов регрессии, оценить качество полученного регрессионного уравнения. Вообще говоря, перед проверкой значимости и качества уравнения необходимо провести тесты на выполнение основных предпосылок линейной регрессионной модели (гомоскедастичность, отсутствие автокорреляции). На данном этапе мы будем считать эти тесты проведенными и вернемся к вопросам выполнения предпосылок ЛРМ позднее.
3. ТЕСТ ФИШЕРА (FISHER TEST) Для начала проверим гипотезу о незначимости регрессии в целом. Тест позволит понять, является ли построенная модель адекватной с точки зрения статистики. Для этой цели воспользуемся тестом Фишера [3]. Тест Фишера (Fisher test) позволяет проверить незначимость регрессии в целом, то есть установить, равны ли коэффициенты одновременно при всех регрессорах нулю. Если коэффициенты признаются равными нулю, регрессия считается незначимой, если коэффициент хотя бы при одном регрессоре отличен от нуля, регрессия значима. Гипотезы
как минимум один из коэффициентов отличен от нуля
Правило принятия решения (гипотеза H0 отвергается, если):
Расчетная статистика
, , где RSS – сумма квадратов остатков, обусловленная регрессией; ЕSS – сумма квадратов остатков, обусловленная ошибками
где n – число наблюдений; k – число регрессоров; – уровень значимости
Сформулируем гипотезы для проверки незначимости регрессии в целом в рассматриваемом примере [файл с данными wage1.gdt] модели , : как минимум один из коэффициентов отличен от нуля. Для принятия решения о том, какую гипотезу нужно отвергнуть, построим F-статистику. Для этого нам должны быть известны (помимо уже имеющихся параметров n — объем выборки и k — число регрессоров в модели) величины RSS и ESS. В явном виде в распечатке на рис. 2.2 дано значение ESS — сумма квадратов остатков, которая составляет ESS = 4966,3 , а также из распечатки известен коэффициент детерминации (подробнее о коэффициенте детерминации и его интерпретации можно прочесть в §7).
10
•
А. С. Малова. Основы эконометрики в среде GRETL
,1 а
Если вспомнить, что
,
то можно путем простых алгебраических преобразований найти необходимую нам величину RSS. При этом сюда можно вычислить
. От.
Критическое значение F-статистики возьмем на уровне значимости 5%: (чтобы получить это значение, в основном меню GRETL нужно выбрать Инструменты — Критические значения — Фишера и ввести необходимое число степеней свободы и правостороннюю вероятность либо посмотреть в статистических таблицах распределения Фишера для уровня значимости 5%, например в [7]).
Рис. 3.1
Рис. 3.2
Уровень значимости, на котором принимается решение о том, какую гипотезу не отвергать, остается на усмотрение исследователя. Как правило, если нет представления, какой именно уровень значимости брать, предлагается выбирать 5%. В случаях работы с маленьким по объему выборками (от 30 до 100 наблюдений) предлагается брать уровень значимости 10%. Для больших выборок (более 1000 наблюдений) можно
1 Второе равенство есть константа.
верно только в том случае, если в регрессии
•
3. Тест Фишера (Fisher test)
11
взять уровень значимости 1%. В нашем случае объем выборки средний (526 наблюдений, эта информация дана в первой строке распечатки на рис. 2.2.), поэтому можно было принять . Сравниваем расчетное значение F-статистики с критическим , то есть 78,2 > 2,6. Следовательно, можно сделать вывод, что гипотеза о незначимости регрессии в целом отвергается. Тест Фишера можно провести также в полуавтоматическом режиме и в автоматическом режиме. Полуавтоматический режим состоит в том, что нам не нужно вручную вычислять значение расчетной F-статистики, оно дано в распечатке на рис. 2.2. В этом случае нужно лишь выяснить критическое значение F-статистики и сравнить расчетное значение с критическим. В автоматическом режиме нужно также воспользоваться распечаткой GRETL и посмотреть на р-значение статистики Фишера на рис. 2.2 (в распечатке р-значение (F)). В р-значении содержится вероятность ошибки I рода. Таким образом, р-значение (F) для теста Фишера — это вероятность ошибки I рода при тестировании гипотезы . По существу это вероятность ошибиться, отвергнув гипотезу H0. Для принятия решения, можно ли отвергнуть гипотезу H0, нужно сравнить р-значение с заданным уровнем значимости . Уровень значимости задает вероятность ошибки I рода, то есть, грубо говоря, какую долю ошибок мы готовы себе позволить, отвергнув гипотезу H0. Если р-значение меньше принятого уровня значимости, то маловероятно, что мы ошибемся, отвергая гипотезу H0 в ситуации, когда р-значение больше уровня значимости, вероятна ошибка в случае отклонения нулевой гипотезы, поэтому ее стоит принять. Отсюда можно сделать вывод, что р-значение показывает вероятность ошибиться, отвергнув гипотезу H0, при том, что она верна. Эта интерпретация р-значения справедлива для всех статистических тестов, и мы будем иметь ее в виду в дальнейшем. В данном случае р-значение (F) (р-значение (F) в распечатке представляет собой «3,41e-41» — это компьютерный способ записи числа , которое практически равно 0). Это говорит о том, что можно отвергнуть гипотезу H0 (вероятность ошибки близка к 0). Стоит обратить внимание еще на один полезный факт. При расчете F-статистики вручную мы использовали формулу Используя соотношение
.
, можно переписать рас-
четную статистику через коэффициент детерминации, не используя квадраты остатков
.
4. ТЕСТ СТЬЮДЕНТА (T-TEST) После того как мы проверили незначимость регрессионного уравнения в целом, рассмотрим, как проверять незначимость коэффициентов при отдельных регрессорах. Для этой цели воспользуемся тестом Стьюдента [3]. Тест Стьюдента (t-test) позволяет проверить незначимость отдельного коэффициента при регрессоре, то есть установить, равен ли коэффициент при соответствующем регрессоре нулю. Если коэффициент признается равным нулю, то регрессор считается незначимым, если коэффициент отличен от нуля — регрессор значим. Гипотезы
Расчетная статистика
Правило принятия решения (гипотеза H0 отвергается, если):
, где n — число наблюдений; k — число регрессоров в модели, для которой проводится исследование; — уровень значимости
Проверим незначимость коэффициента при переменной . Сформулируем гипотезы теста для указанной переменной [файл с данными wage1.gdt]. Они будут выглядеть следующим образом:
Значение оцененного коэффициента при этой переменной находится в столбце «Коэффициент» — . Для того чтобы вычислить расчетную t-статистикy, необходимо знать значение стандартной ошибки для коэффициента, оно содержится в столбце «Ст. ошибка». Для переменной стандартная ошибка . Отсюда можем вычислить
•
4. Тест Стьюдента (t-test)
13
. Для принятия решения о том, можно ли отвергнуть гипотезу H0 , сравним значение стики
с критическим значением стати-
. Примем уровень значимости
. Как уже было
сказано, объем выборки составляет 526 наблюдений, то есть n = 526. Число регрессоров в модели составляет 4 (константа тоже регрессор), то есть, k = 4. Отсюда следует, что нужно искать критическое значение из двустороннего распределения Стьюдента на уровне значимости 5% (одностороннее распределение 2,5%) с 522 степенями свободы. Для поиска критического значения из распределения Стьюдента можно воспользоваться статистическими таблицами, например из [7]. Но можно воспользоваться возможностями GRETL. Для этого в основном меню выберем Инструменты — Критические значения.
Рис. 4.1
В открывшемся окне «Критические значения» выберем вкладку, соответствующую распределению Стьюдента, и введем нужные параметры распределения.
Рис. 4.2
14
•
А. С. Малова. Основы эконометрики в среде GRETL
Стоит обратить внимание на то, что в GRETL предполагается для распределения Стьюдента вводить не двустороннюю вероятность, а только правостороннюю вероятность, то есть в нашем случае это 2,5%. После нажатия клавиши ОК получаем искомое критическое значение .
Рис. 4.3
После этого сравниваем расчетное и критическое значение статистик для переменной . В нашем случае (|11,68| > 1,96), отсюда можно сделать вывод, что гипотеза H0 отвергается, то есть можно говорить о том, что регрессор значим. Рассмотренный способ проверки гипотезы незначимости коэффициента при отдельном регрессоре позволяет соотнести теоретические знания о проверке незначимости с практикой. Однако ту же самую процедуру можно несколько упростить. Обратим внимание, что в столбце t-статистика для всех переменных уже указаны расчетные значения статистики. Так, например, для переменной указано полученное нами значение . Это несколько сокращает процедуру проверки, однако сравнение расчетного и критического значения t-статистики все же приходится проделывать самостоятельно. Существует еще более простой и быстрый способ проверки незначимости коэффициента. В рассматриваемом примере p-значение переменной составляет , то есть практически равно 0. В этом случае, p-значение переменной меньше заданного уровня значимости . Это значит, что можно отвергнуть гипотезу H0, то есть коэффициент при регрессоре значим. Аналогичную проверку незначимости мы можем провести для коэффициентов остальных регрессоров. На 5%-ном уровне значимости можно утверждать, что коэффициент при и константа — значимы, коэффициент при на 5%-ном уровне не значим, однако он является значимым на 10%-ном уровне значимости.
•
4. Тест Стьюдента (t-test)
15
Задание для самостоятельной работы Выпишите гипотезы для проверки незначимости коэффициентов при регрессорах , и для константы. Постройте расчетные значения t-статистики для указанных регрессоров и найдите критическое значение t-статистики для 10%-го уровня значимости. Сравните полученные значения расчетных t-статистик с теми, которые указаны в распечатке на рис. 2.2. Сделайте вывод о незначимости регрессоров, основываясь на сравнении расчетной статистики и критической.
В программе GRETL предусмотрена визуализация значимости коэффициентов при отдельных регрессорах на разных уровнях значимости. Для этого справа от каждого регрессора расположены звездочки: • Наличие одной звездочки говорит о том, что коэффициент значим только на 10%-ном уровне. • Наличие двух звездочек говорит о значимости коэффициента на 5%-ном уровне. • Три звездочки информируют о значимости коэффициента на 1%-ном уровне. • Отсутствие звездочек говорит о незначимости коэффициента на 10%-ном уровне. Мы проверили незначимость коэффициентов при всех регрессорах, включенных в модель. Если мы хотим ориентироваться на 5%-ный уровень значимости, то нужно удалить переменную с незначимым коэффициентом. Для того чтобы это сделать в окне с построенной моделью (в нашем случае это окно Модель 1, но, вообще говоря, это может быть Модель № в зависимости от того, сколько вы моделей построили до этого), выбираем пункт меню Правка — Изменить модель.
Рис. 4.4
В открывшемся окне выделяем переменную удаляем ее из независимых переменных.
и красной стрелкой
16
•
А. С. Малова. Основы эконометрики в среде GRETL
Рис. 4.5
Обновленная модель представлена на рис. 4.6.
Рис. 4.6
Как видно из распечатки, все коэффициенты регрессии в обновленной модели значимы на 1%-ном уровне (следовательно, и на 5%-ном уровне они тоже значимы). Возможности t-теста не ограничиваются только проверкой незначимости коэффициентов при регрессорах. На самом деле проверка незначимости коэффициента является частным случаем проверки равенства коэффициента при регрессоре конкретному значению [2, 3].
•
4. Тест Стьюдента (t-test)
17
Тест Стьюдента (t-test) позволяет проверить, равен ли коэффициент при соответствующем регрессоре некоторому значению, определенному исследователем. Гипотезы
Расчетная статистика
Правило принятия решения (гипотеза H0 отвергается, если):
, где n — число наблюдений; k — число регрессоров в модели; — уровень значимости
Разберем это на примере. Проверим, а можем ли мы округлить коэффициент при переменной до 0,2. Сформулируем гипотезы для проверки этого предположения:
Для проверки такого рода гипотезы уже нельзя воспользоваться рассчитанным в GRETL значением t-статистики, а также р-значением, поэтому вычислим значение t-статистики для переменной самостоятельно:
. Значение критической
точки Стьюдента составит
.
Сравниваем расчетную статистику и критическую и получаем, что , то есть (|–0,56| < 1,96). В этом случае, мы можем принять нулевую гипотезу и округление коэффициента перед до 0,2 будет статистически корректно. Аналогичные гипотезы мы можем проверять для остальных коэффициентов регрессии. Задание для самостоятельной работы Проверьте, можно ли округлить коэффициент при переменной до 0,5 на 5%-ном уровне значимости. Выпишите гипотезы, рассчитайте статистики и сделайте содержательный вывод.
Проверить, может ли коэффициент при регрессоре равняться заданному значению, позволяет также доверительный интервал [2, 3].
18
•
А. С. Малова. Основы эконометрики в среде GRETL
Доверительный интервал для оценки коэффициента позволяет определить границы, в которых истинное значение коэффициента находится с вероятностью 1 – , где — уровень значимости. , где
— оценка для коэффициента,
ненная стандартная ошибка для оценки коэффициента, значение статистики Стьюдента.
— оце-
— критическое
Используя данные из распечатки на рис. 4.6, можно построить доверительные интервалы для всех коэффициентов самостоятельно либо воспользоваться встроенной функцией GRETL для построения доверительного интервала. Для этого в окне модели вызовем пункт меню Анализ — Доверительные интервалы для коэффициентов.
Рис. 4.7
Результатом работы данной функции является следующее окно (рис. 4.8).
Рис. 4.8
Истинное значение коэффициента при переменной ятностью 95% накрывается интервалом .
с веро-
Задание для самостоятельной работы Посчитайте вручную 95%-ный доверительный интервал для коэффициента при переменной и сравните с доверительным интервалом, полученным в GRETL.
•
4. Тест Стьюдента (t-test)
19
Нужно обратить внимание на то, что с помощью доверительного интервала можно проверять незначимость коэффициентов при регрессорах. В случае, если доверительный интервал накрывает 0 (то есть истинное значение коэффициента может принимать нулевое значение), можно сделать вывод о том, что коэффициент не значим. Еще одна возможность для проверки гипотез с помощью теста Стьюдента — это односторонние гипотезы [2, 3]. Односторонний тест Стьюдента (one-sided t-test) позволяет проверить гипотезу о равенстве оценки коэффициента конкретному значению против гипотезы о том, что оценка коэффициента больше либо меньше соответствующего значения. Гипотезы
Расчетная статистика
Правило принятия решения (гипотеза H0 отвергается, если):
,
где n — число наблюдений; k — число регрессоров; — уровень значимости
Разберем, как проводится односторонний t-тест на примере. Проверим, верно ли, что коэффициент перед переменной можно считать большим 0,2.
Значение расчетной статистики для этого теста будет такое же, как и в предыдущем тесте (проверка равенства коэффициента заданному значению). Критическая точка составит . Сравнивая расчетное значение статистики с критическим, получаем , то есть –0,56 < 1,65. Значит, гипотеза H0 принимается. По сути, все разновидности t-теста и построение доверительного интервала для коэффициента — это две стороны одной медали. Полезные результаты можно получать и тем и другим способом, выбор способа ответа на вопросы о незначимости коэффициента при регрессоре и соотношения коэффициента регрессора с заданным значением возлагается на исследователя.
5. ПРОВЕРКА ГИПОТЕЗЫ О СОВМЕСТНОЙ НЕЗНАЧИМОСТИ КОЭФФИЦИЕНТОВ В рассматриваемой нами модели зависимости заработной платы после проверки незначимости коэффициентов при отдельных регрессорах осталось две независимых переменных: образование и опыт работы у текущего работодателя. Однако с экономической точки зрения очевидно, что на уровень заработной платы сотрудника могут влиять и некоторые другие факторы, например, уровень интеллекта (IQ), возраст, образование и заработок родителей, общий уровень знаний и проч. Когда мы отбираем регрессоры для модели, мы, с одной стороны, должны руководствоваться соображениями экономической обоснованности и осмысленности, а с другой — нужно иметь в виду и эконометрические аспекты. Так, например, нужно помнить, что если не включить существенные регрессоры в модель, оценка для дисперсии ошибок модели получится смещенная, и тогда тесты на незначимость будут работать некорректно. Если же включить несущественную переменную, оценки для коэффициентов хоть и будут несмещенные, но получатся неэффективными. Таким образом, отбирая регрессоры для модели, нужно учитывать как содержательные аспекты, так и эконометрические. Предположим, что с точки зрения экономического смысла мы определились с регрессорами и решили построить следующую модель [файл с данными wage2.gdt]: , где — средняя заработная плата в месяц в долларах, — среднее число рабочих часов в неделю, — уровень IQ в баллах, — индекс знания своей области деятельности в баллах, — уровень образования в годах, — опыт работы в годах, — опыт работы у текущего работодателя в годах, — образование матери, — образование отца1. На рис.5.1 дана распечатка оцененной регрессии. По распечатке можно сделать вывод, что в целом регрессия значима, но не все коэффициенты значимы по отдельности. 1 В файле wage2.gdt есть пропущенные наблюдения. Перед тем как проводить процедуру тестирования наблюдения с пропусками в регрессорах, и были удалены.
5. Проверка гипотезы о совместной незначимости коэффициентов
•
21
Задание для самостоятельной работы Проверьте гипотезы о незначимости регрессии в целом и отдельных регрессоров на 1, 5 и 10%-ном уровнях значимости.
На 5%-ном уровне значимости сразу несколько коэффициентов перестают быть значимыми. Если бы не значим был лишь один коэффициент в модели, его можно было бы исключить, но в случае незначимости нескольких коэффициентов можно ли исключить соответствующие регрессоры из модели на том основании, что коэффициент каждого из них в отдельности не значим на 5%-ном уровне? Чтобы ответить на этот вопрос, нужно вспомнить о том, что существенные регрессоры исключать из модели некорректно, но оставлять несущественные регрессоры в модели тоже не является правильным. Поэтому для того, чтобы понять, можно ли исключить все регрессоры, чьи коэффициенты не значимы на 5%-ном уровне, или нужно исключить только некоторые из них и какие именно, необходимо провести тест на совместную незначимость коэффициентов при регрессорах [2, 3]. Тест Фишера (Fisher test) на совместную незначимость позволяет проверить незначимость нескольких коэффициентов в модели, то есть установить, равны ли коэффициенты одновременно при этих регрессорах нулю. Если коэффициенты признаются одновременно равными нулю, эти регрессоры считаются незначимыми совместно и могут быть исключены из регрессии, если коэффициент хотя бы при одном регрессоре отличен от нуля, регрессоры совместно значимы и нужно проводить дальнейший анализ, чтобы понять, какие именно регрессоры из незначимых в отдельности можно исключить из модели. Гипотезы
Правило принятия решения (гипотеза H0 отвергается, если):
Расчетная статистика
, где — сумма квадратов остатков для модели с ограничением (модели, в которой все регрессоры, подозрительные на совместную незначимость коэффициентов, исне так ключены); — сумма квадратов остат(хотя бы один ков для модели без ограничения коэффициент отличен (модели, в которую все регрессоры, подозрительные на совместную от нуля) незначимость коэффициентов, включены); q — количество подозрительных на совместную незначимость регрессоров
где q — количество регрессоров, подозрительных на совместную незначимость коэффициентов; n — число наблюдений; k — число регрессоров в исходной модели, то есть модели, в которую включены все регрессоры и со значимыми коэффициентами и, возможно, с совместно незначимыми
22
•
А. С. Малова. Основы эконометрики в среде GRETL
Данный тест можно проводить несколькими способами в GRETL, рассмотрим каждый из них на примере рассматриваемой модели. Сформулируем гипотезу о совместной незначимости регрессоров , . не так Результаты оценивания регрессии без ограничения приведены на рис. 5.1, сумма квадратов остатков данной модели .
Рис. 5.1
Оценим регрессию с ограничением, то есть исключим из нее переменные с коэффициентами, подозрительными на совместную незначимость. Для этого можно, очевидно, по новой оценить модель, но можно и в существующей модели выбрать пункт меню Правка — Изменить модель и удалить регрессоры с коэффициентами, подозрительными на совместную незначимость. Результат оценивания модели с ограничением представлен на рис. 5.2. Сумма квадратов остатков в модели с ограничением . Далее рассчитаем значение F-статистики:
.
Критическое значение статистики составляет , таким образом, , гипотеза о совместной незначимости коэффициентов при этих регрессорах на 5%-ном уровне значимости
5. Проверка гипотезы о совместной незначимости коэффициентов
•
23
принимается. Оба регрессора могут быть исключены из модели, и тогда окончательной спецификацией будет модель с ограничением: .
Рис. 5.2
Тест на совместную незначимость коэффициентов также можно провести автоматически. Для этого, после того как было оценено исходное уравнение, в меню окна результатов нужно выбрать Тесты — Избыточные переменные.
Рис. 5.3
После этого в меню можно выбрать одну из опций оценивания: оценить сокращенную модель (аналог того теста, который был показан выше) или проверить избыточность переменных с использованием теста Вальда [9].
24
•
А. С. Малова. Основы эконометрики в среде GRETL
Результат оценивания с использованием сокращенной модели представлен на рис. 5.4.
Рис. 5.4
При данном методе проверки также рассчитывается F-статистика и ее значение совпадает с тем, что было получено вручную. При этом приводится оцененный вариант короткой модели (модели с ограничением). Нулевая гипотеза состоит в том, что указанные на этапе тестирования переменные нулевые. Для проверки этой гипотезы можно воспользоваться рассчитанным значением F-статистики и сравнить его с критической точкой, как это было проделано, а можно обратить внимание на р-значение = 0,254184, то есть вероятность ошибиться, отвергнув нулевую гипотезу о незначимости коэффициентов, составляет примерно 0,26. Так как р-значение > 0,05 (больше зафиксированного уровня значимости), мы принимаем нулевую гипотезу, указанные коэффициенты не значимы на 5%-ном уровне, и соответствующие регрессоры нужно исключить из модели. Корректный вариант модели — модель с ограничением. Аналогично можно провести тест на избыточные переменные, используя тест Вальда (рис. 5.5).
Рис. 5.5
Результаты тестирования полностью совпадают с предыдущими вариантами теста.
6. ПРОВЕРКА ПРАВИЛЬНОСТИ СПЕЦИФИКАЦИИ МОДЕЛИ (RESET TEST) Для проверки правильности спецификации линейной регрессионной модели используется RESET-тест. Он позволяет определить, помогает ли нелинейная комбинация оцененного значения зависимой переменной лучше объяснить изменения самой зависимой переменной. Если качество объяснения при этом улучшается, значит, модель специфицирована неправильно [9]. RESET-тест Рамсея на правильность спецификации позволяет определить, помогает ли нелинейная комбинация оцененного значения зависимой переменной лучше объяснить изменения самой зависимой переменной. Если качество объяснения при этом улучшается, значит, модель специфицирована неправильно. Гипотезы
не так где коэффициенты регрессии
Расчетная статистика
, где — сумма квадратов остатков для модели без оцененных зависимых переменных в качестве регрессоров; — сумма квадратов остатков для модели с оцененными зависимыми переменными в качестве регрессоров; l — количество регрессоров, которые являются степенями прогнозного значения зависимой переменной
Правило принятия решения (гипотеза H0 отвергается, если):
где l — количество регрессоров, которые являются степенями прогнозного значения зависимой переменной; n — число наблюдений; k — число регрессоров в исходной (тестируемой) модели
26
•
А. С. Малова. Основы эконометрики в среде GRETL
Проведем RESET-тест для модели , то есть проверим правильность спецификации этой модели [файл с данными wage2.gdt]. Оценим предложенную регрессию и сохраним оцененные значения зависимой переменной. Для этого в окне с результатами оценки выберем пункт меню Сохранить — Расчетные значения.
Рис. 6.1
После этого включим степени расчетных значений зависимой переменной в качестве регрессоров. Как правило, число степеней может равняться числу регрессоров в исходной модели, но начинать можно и с меньшего количества. Добавить новые переменные (степени расчетных значений зависимой переменной) можно через основное меню Добавить — Добавить новую переменную и ввести формулу, можно для четных степеней воспользоваться функцией меню Добавить — Квадраты выделенных переменных, а можно прямо в окне для оценки регрессии выбрать кнопку (+), которая позволит тут же создать новую переменную.
Рис. 6.2
Результат оценки регрессии с учетом степеней расчетных значений зависимой переменной представлен на рис. 6.3.
6. Проверка правильности спецификации модели (RESET test)
•
27
Рис. 6.3
Как видно из распечатки на рис. 6.3, все коэффициенты в модели стали незначимы, вновь добавленные регрессоры имеют также незначимые коэффициенты. Проведем формальный тест на совместную незначимость с использованием встроенных средств GRETL.
Рис. 6.4
По результатам теста р-значение < 5%, то есть можно отвергнуть нулевую гипотезу о совместной незначимости коэффициентов при вновь добавленных регрессорах, хотя бы один из коэффициентов при добавленных трех регрессорах значим. Из эмпирических соображений попробуем исключить последний регрессор — четвертую степень для расчетных значений зависимой переменной — и оценим модель без него.
Рис. 6.5
28
•
А. С. Малова. Основы эконометрики в среде GRETL
Все коэффициенты, кроме константы, стали значимы на 10%-ном уровне значимости, то есть наличие в регрессии степеней прогнозного значения зависимой переменной если не улучшает качество регрессии, то по крайней мере не ухудшает его, что говорит о наличии системных недочетов в спецификации данной модели. Как и все рассматриваемые в данном пособии тесты, RESET-тест можно проводить с помощью встроенной процедуры GRETL. Для этого после этапа оценки регрессии в меню оцененной модели выбираем Тест — тест Рамсея (RESET). В выпадающем меню выбираем вариант тестирования с квадратами и кубами.
Рис. 6.6
Результаты тестирования представлены на рис. 6.7 и совпадают с проведением вручную теста на совместную незначимость для коэффициентов при дополнительных регрессорах.
Рис. 6.7
р-значение для теста Рамсея позволяет сделать вывод о том, что гипотезу H0 нужно отвергнуть, спецификация модели нуждается в корректировке.
7. ПРОВЕРКА КАЧЕСТВА РЕГРЕССИОННОЙ МОДЕЛИ… (КОЭФФИЦИЕНТ ДЕТЕРМИНАЦИИ), ИНФОРМАЦИОННЫЕ КРИТЕРИИ После того как мы провели тест Фишера и убедились в том, что регрессия в целом значима, а также определились с тем, какие регрессоры необходимо оставить в модели, перейдем к оценке качества модели. Для начала рассмотрим понятие качества подгонки модели. Оно связано с возможностью регрессоров объяснять зависимую переменную. Под объяснением в данном случае понимается возможность по изменениям в регрессорах корректно предсказывать изменения в зависимой переменной. Понятие качества подгонки модели в англоязычных учебниках называется Goodness of Fit, или GoF. Для построения статистики Фишера мы уже использовали так называемый коэффициент детерминации [3, 9]. Определение
Коэффициент детерминации ( ) показывает, какая доля (можно говорить в %) дисперсии зависимой переменной объясняется регрессионным уравнением. Коэффициент детерминации изменяется от 0 до 1 при наличии константы в модели (от 0% до 100%), при этом чем ближе его значение к 1 (100%), тем лучше считается качество модели (то есть большая доля дисперсии зависимой переменной объясняется регрессионным уравнением.
Формула
RSS — сумма квадратов остатков, обусловленная регрессией; ESS — сумма квадратов остатков, обусловленная ошибками; TSS — общая сумма квадратов остатков регрессии
Значение для построенной нами модели [файл с данными wage1.gdt] уже было выписано в явном виде из распечатки GRETL для проведения теста Фишера (рис. 2.2). С точки зрения интерпретации можно сказать следующее: значение коэффициента детерминации нельзя назвать высоким, лишь 31% изменений в заработной плате объясняются изменениями в образовании человека и его опытом у данного работодателя, остальные 69%, видимо, объясняются другими аспектами. Однако делать вывод о том, что модель не пригодна для анализа и бесполезна, тоже не стоит — результаты просто показывают относительно
30
•
А. С. Малова. Основы эконометрики в среде GRETL
небольшой вклад образования и опыта работы у текущего работодателя в объяснение заработной платы. Стоит сказать, что на практике не всегда удается получить коэффициент детерминации, очень близкий к 1 (скажем, 0,95 или 0,99), но желательно стремиться к тому, чтобы значение было близко к 1. Что можно сделать, чтобы улучшить значение ? Скорее всего, добавить к существующим регрессорам еще какие-то переменные, которые содержали бы больше информации, либо вовсе заменить имеющиеся у нас регрессоры другими, оказывающими более существенное влияние на зависимую переменную. Однако здесь следует помнить о том, что при добавлении новых регрессоров в модель будет только расти, и даже если добавить регрессор с незначимым коэффициентом, который ничуть не улучшает объяснение дисперсии зависимой переменной, вырастет. Примером могут служить уравнения и [файл с данными wage1.gdt].
Рис. 7.1
Коэффициент детерминации для уравнения с четырьмя регрессорами составляет , а коэффициент детерминации для уравнения с тре-
• 31
7. Проверка качества регрессионной модели…
мя регрессорами несколько меньше. Для того чтобы иметь возможность сравнивать качество регрессий с разным числом объясняющих переменных, используют скорректированный коэффициент детерминации . Если принять уровень значимости не 5%, а 10%, то обе регрессии становятся сопоставимы и возникает необходимость выбрать, какая из них обеспечивает лучшее качество модели. Сравним скорректированные коэффициенты детерминации для обеих моделей. Скорректированный коэффициент детерминации находится в строке Испр. R-квадрат. Для , а для второй регрессии — первой регрессии он составляет . Мы видим, что качество первой модели, исходя из скорректированного коэффициента детерминации, чуть лучше, чем второй. Для сравнения моделей между собой с целью выбора наилучшей можно использовать так называемые информационные критерии [7]. Наиболее распространенным и известным является критерий Акаике (AIC — Akaike Information Criterion). Определение
Информационный критерий Акаике (AIC) — показывает степень качества модели (goodness of fit) и при этом вводит штрафную функцию за переизбыток регрессоров в модели. При прочих равных условиях стоит предпочитать модель, в которой значение AIC более низкое.
Формула
где k — число регрессоров модели; L — функция максимума правдоподобия для оцениваемой модели
Сравним по критерию Акаике модели, оцененные на рис. 7.1. Соответствующие данные представлены в распечатках в графе Крит. Акаике. Для первой модели , для второй модели — . По критерию Акаике первая модель лучше второй, так как информационный критерий для нее меньше. Второй популярный критерий, аналогичный критерию Акаике, это критерий Хеннана-Куинна (Hannan-Quinn information criterion — HQC). Определение
Информационный критерий Хеннана-Куинна (HQC) — при прочих равных условиях стоит предпочитать модель, в которой значение HQC более низкое.
Формула
, где k — число регрессоров модели; RSS — сумма квадратов остатков, обусловленная регрессией; n — число наблюдений
32
•
А. С. Малова. Основы эконометрики в среде GRETL
Если сравнить первую и вторую модели по критерию Хеннана– Куинна (графа в распечатках на рис. 7.1 Крит. Хеннана–Куинна), и . Значения критерия для двух моделей практически равно, различия на уровне десятых долей, однако в пользу второй модели (напомним, что по критерию Акаике лучшей была признана первая модель). Еще один широко используемый информационный критерий — это Байесовский информационный критерий (Bayesian Information Criterion — BIC), он еще носит название критерия Шварца (Schwarz criterion — SC). Определение
Информационный критерий Шварца (SC) Байесовский информационный критерий (BIC) — при прочих равных условиях стоит предпочитать модель, в которой значение SC/BIC более низкое.
Формула
где k — число регрессоров модели; L — функция максимума правдоподобия для оцениваемой модели
Информационный критерий Шварца для первой модели составляет , для второй модели . По критерию Шварца также получается, что первая модель лучше второй. Резюме вышеизложенного следующее. Существуют три информационных критерия для сравнения регрессионных моделей с целью выбора наилучшей. Для принятия решения можно руководствоваться результатами всех трех критериев и выбирать ту модель, в которой хотя бы два из трех критериев имеют наименьшее значение.
8. ИНТЕРПРЕТАЦИЯ КОЭФФИЦИЕНТОВ РЕГРЕССИИ И ПРОГНОЗИРОВАНИЕ По распечатке, представленной на рис. 2.2, было выписано регрессионное уравнение [файл с данными wage1.gdt]: . После этого, используя тест Стьюдента, мы исключили регрессор, коэффициент при котором был не значим на 5%-ном уровне значимости, и результат оценивания регрессии содержится в распечатке GRETL на рис. 8.1.
Рис. 8.1
Рассмотрим подробнее рис. 8.1. Нет никакой необходимости выписывать коэффициент с точностью до 6-го знака после запятой. В большинстве случаев достаточно округления до сотых или до десятых, в зависимости от того, что удобнее и какая степень точности нужна и какова точность исходных данных. В рассматриваемом случае удобно округлить до сотых . Опираясь на значения коэффициентов в регрессии, мы можем выписать оцененное регрессионное уравнение, а также дать интерпретацию коэффициентам модели: . Данному уравнению можно дать следующую интерпретацию: при росте уровня образования человека на 1 год его зарплата вырастет в среднем на 57 центов в час при фиксированном стаже; при росте стажа у текущего работодателя на 1 год заработная плата вырастет в среднем на 19 центов в час при фиксированном уровне образования. Если обобщить, то интерпретация коэффициентов регрессионного уравнения дается в на-
34
•
А. С. Малова. Основы эконометрики в среде GRETL
туральных единицах измерения регрессоров и зависимой переменной, при этом произвольный коэффициент показывает размер изменения зависимой переменной (в единицах измерения зависимой переменной) при изменении регрессора на единицу (в единицах измерения регрессора). Константа в регрессионном уравнении обычно присутствует, но не всегда может быть интерпретирована. Если, как в данном примере, с точки зрения здравого смысла интерпретация константы не разумна, просто не нужно ее интерпретировать. В общем же случае константа показывает, каково среднее значение зависимой переменной при нулевых регрессорах. Одной из задач построения эконометрических моделей в целом и регрессионных уравнений в частности является прогнозирование. Для оцененной нами модели мы можем также построить прогноз как автоматически, так и в ручном режиме. Допустим, мы хотели бы узнать размер заработной платы для специалиста с образованием 15 лет (то есть ) с опытом у текущего работодателя 5 лет ( . Чтобы построить прогноз вручную, нужно просто подставить соответствующие значения регрессоров в оцененное уравнение регрессии: , то есть заработная плата такого специалиста составит $7,73 в час. Аналогично можно построить прогноз и с использованием GRETL. Для этого добавляем в выборку новое наблюдение, чтобы ввести необходимые данные (если нам нужно построить прогноз на несколько шагов вперед, добавляем несколько наблюдений): Данные — Добавить наблюдения. В появившемся окне вводим количество новых наблюдений, в данном случае одно. Теперь выборка стала не 526 наблюдений, как была, а 527. Вводим значения 527-го наблюдения для каждого из регрессоров. Для этого выбираем регрессор, кликаем на него правой кнопкой мыши, чтобы появилось контекстное меню, и нажимаем Изменить значения (рис. 8.2).
Рис. 8.2
8. Интерпретация коэффициентов регрессии и прогнозирование
•
35
После этого в появившемся окне вводим нужное значение регрессора (в данном случае 15) и сохраняем изменения в переменной, нажав на зеленую галочку в меню (рис. 8.3).
Рис. 8.3
Аналогично добавляем значение нового наблюдения в переменную . Далее оцениваем регрессию и выбираем в меню с результатами оценивания Анализ — Прогнозы.
Рис. 8.4
36
•
А. С. Малова. Основы эконометрики в среде GRETL
Горизонт прогнозирования автоматически включает в себя вновь добавленное наблюдение, прогноз статический. Результаты прогнозирования представлены в виде количественных значений прогноза.
Рис. 8.5
9. ОЦЕНКА РЕГРЕССИИ В ЛОГАРИФМАХ И ИНТЕРПРЕТАЦИЯ Существует три типа регрессий в логарифмах [9]: •логарифмические модели (log-log models): •линейно-логарифмические модели (linear-log models): ; •лог-линейные модели (log-linear models):
Рис. 9.1
;
.
38
•
А. С. Малова. Основы эконометрики в среде GRETL
Логарифмические преобразования переменных очень часто необходимы для того, чтобы работать с ситуациями нелинейной зависимости между регрессором и регрессандом. Логарифмирование позволяет перейти к анализу линейной модели без потери информации, когда в действительности анализируется нелинейная зависимость. Вторая распространенная причина логарифмирования переменных — необходимость избавиться от смещения в наблюдениях. Очень часто, например, доход имеет смещение в сторону меньших значений, и логарифмирование позволяет привести наблюдения к распределению, более похожему на нормальное. Примером может служить переменная , которая до логарифмирования имеет смещение влево (рис. 9.1, вверху), а после логарифмирования становится «похожа» на нормальное распределение. Чтобы прологарифмировать переменную в GRETL, можно воспользоваться встроенной командой меню Добавить — Логарифм выделенных переменных. Для этого выделяем нужную переменную (ые) и вызываем данную команду либо можно создать переменную вручную Добавить — Добавить новую переменную и написать функцию , где — это имя новой создаваемой переменной (рис. 9.2).
Рис.9.2
Оценивание регрессионных уравнений с разными типами логарифмических зависимостей происходит одинаково, так как это один и тот же класс линейных регрессионных моделей, однако различия заключаются в интерпретации коэффициентов каждой из модели. Тип модели
Вид уравнения
Интерпретация
Логарифмические модели (log-log models)
При увеличении переменной на 1% в среднем y изменится на
Линейнологарифмические модели (linear-log models)
При увеличении
на 1% y
изменится в среднем на натуральных единиц
•
9. Оценка регрессии в логарифмах и интерпретация
39
Окончание табл. Тип модели
Лог-линейные модели (log-linear models)
Вид уравнения
Интерпретация
При увеличении на единицу y в среднем изменится на
Стоит сказать, что приведенная интерпретация работает в случае, если значения оцененных коэффициентов достаточно малы. Более точные варианты интерпретации можно узнать в [9].
10. ПРОВЕРКА ЛИНЕЙНЫХ ОГРАНИЧЕНИЙ НА КОЭФФИЦИЕНТЫ РЕГРЕССИИ Общим случаем теста на совместную незначимость коэффициентов при регрессорах является тест для проверки линейных ограничений. Линейное ограничение для коэффициентов регрессоров — это совокупность линейных комбинаций регрессоров, приравненных к некоторым величинам. Например, равенство двух регрессоров ( может быть представлено как выражение либо может быть предложено для проверки сразу два линейных ограничения, и . Идея проверки гипотез о линейных ограничениях сводится к тому, чтобы проверить, выполняются ли все ограничения вместе или нет [2, 3]. Тест Фишера (Fisher test) для линейных ограничений позволяет ответить на вопросы о том, связаны ли оценки коэффициентов регрессии между собой некоторым линейным соотношением. Гипотезы
Расчетная статистика
H0 : линейные ограничения верны H1 : не так
, где — сумма квадратов остатков для модели с ограничением (модели, в которой учтено линейное ограничение для регрессоров); — сумма квадратов остатков для модели без ограничения (модели, которая оценена без учета линейных ограничений); q — количество линейных ограничений
Правило принятия решения (гипотеза H0 отвергается, если):
где q — количество линейных ограничений; n — число наблюдений; k — число регрессоров в исходной модели
Рассмотрим данный тест на примере. Для регрессии, оценка которой приводится на рис. 5.4,
• 41
10. Проверка линейных ограничений на коэффициенты регрессии
. Ответим на вопрос, верно ли, что влияние опыта на размер заработной платы в три раза меньше, чем влияние уровня образования [файл с данными wage2.gdt]. Формально данная гипотеза будет выглядеть представленным ниже образом: не так. Чтобы проверить сформулированные гипотезы без рассмотрения доверительных интервалов для интересующих нас коэффициентов регрессии, нужно провести тест Фишера, аналогичный тесту на совместную незначимость. Вообще говоря, тест на совместную незначимость коэффициентов — это частный случай теста линейных ограничений для коэффициентов модели, в данном методическом пособии они рассматриваются по отдельности исключительно с целью облегчения восприятия информации. Если наложить указанное в нулевой гипотезе ограничение на исходную модель: , то в результате мы получим модель вида
, которая при дальнейшем рассмотрении будет моделью с ограничением. Для проведения теста нам нужно оценить как модель без ограничения (рис. 5.4), так и модель с ограничением. Для того чтобы выполнить последнее, нужно создать новую переменную вида . Это можно сделать через меню основного окна GRETL Добавить — Добавить новую переменную.
Рис. 10.1
42
•
А. С. Малова. Основы эконометрики в среде GRETL
После этого оцениваем модель с вновь созданной переменной, при этом переменные и в регрессию по отдельности не включаются. Результат оценивания приведен на рис. 10.2.
Рис. 10.2
В полученной модели с ограничением все коэффициенты значимы, модель в целом значима. Далее рассчитаем значение F-статистики. , где
,
, q = 1 (так как на коэф-
фициенты было наложено одно ограничение), n = 722, k = 7, таким образом,
,
,
, следовательно, ну-
левая гипотеза принимается, утверждение о том, что влияние опыта на размер заработной платы в три раза меньше, чем влияние уровня образования, верно. Рассмотренный тест можно также провести в автоматическом режиме. Для этого в модели без ограничений откроем меню Тесты — Линейные ограничения и в появившемся окне запишем необходимое линейное ограничение. В GRETL существуют некоторые синтаксические правила для записи такого рода ограничений, а именно, коэффициенты в ограничении записываются в виде , при этом само ограничение формулируется не в виде равенства линейной функции от одних регрессоров линейной функции других регрессоров, а в виде равенства линейной функции от всех регрессоров, на которые наложено ограничение, константе. В нашем примере это ограничение будет выглядеть указанным образом: (рис. 10.3).
10. Проверка линейных ограничений на коэффициенты регрессии
•
43
Рис. 10.3
Результаты проверки данного ограничения представлены на рис. 10.4.
Рис. 10.4
Как видно из распечатки на рис. 10.4, значение расчетной F-статистики совпадает с тем, которое было посчитано вручную, p-значение = 0,56, оно больше уровня значимости, значит, мы с вероятностью 0,56 ошибемся, если отвергнем нулевую гипотезу. Ее нужно принять, влияние опыта на размер заработной платы в три раза меньше, чем влияние уровня образования на размер заработной платы.
11. ФИКТИВНЫЕ ПЕРЕМЕННЫЕ (DUMMY VARIABLES) Фиктивная переменная для одной категории До настоящего момента в основном мы рассматривали в качестве регрессоров и зависимой переменной в модели только количественные переменные, то есть те переменные, отдельные наблюдения которых выражаются некоторой численной величиной. Однако помимо количественных переменных существует еще несколько типов переменных, один из них называется категориальные переменные. Каждое наблюдение переменной также выражается некоторым числом, однако это число не имеет количественной интерпретации, а лишь кодирует некоторую качественную категорию или признак. Например, такое свойство респондента, как пол, может проявляться в двух категориях — «мужской пол» и «женский пол». Мы можем обозначить (закодировать) «мужской пол», единицей, а «женский пол» — двойкой, в результате наблюдения по переменной «пол» будут принимать значения либо один, либо два. Однако если мы попробуем работать с такими данными в регрессионной модели, то могут возникнуть проблемы с интерпретацией результатов. В такой ситуации более эффективно становится несколько изменить кодировку и обозначить «мужской пол», например, через ноль, а «женский пол» — через единицу:
. Дальше мы увидим, что
такую переменную, которая состоит только из нулей и единиц, довольно легко интерпретировать и, следовательно, использовать в моделировании. Такие переменные, которые принимают только два значения, ноль или единица, называются фиктивными переменными (dummy variables). Рассмотрим сквозной пример про заработную плату. Допустим, мы хотели бы узнать, зависит ли в среднем размер заработной платы от семейного положения человека. Введем в рассмотрение переменную . Оценим регрессию с учетом данной переменной:
[файл с данными wage2.gdt].
•
11. Фиктивные переменные (dummy variables)
45
Рис. 11.1
Оцененное уравнение регрессии можно выписать:
Как можно увидеть из распечатки на рис. 11.1, коэффициент при переменной значим, то есть мы можем дать переменной интерпретацию. Для того чтобы лучше понять, как интерпретировать фиктивную переменную, проделаем следующее: предположим, что переменная приняла значение 1. Тогда оцененное уравнение регрессии будет изменено: . Это изменение соответствует тому, что, по сути, к константе было добавлено еще одно значение константы. Если переменная , то есть человек состоит в браке, его заработная плата в среднем увеличивается на 160,7 единиц. Если принять переменную , регрессия будет выглядеть так, будто в ней и нет фиктивной переменной
. В этом случае можно сделать вывод, что заработная плата человека, состоящего в браке, в среднем на 160,7 единиц выше заработной платы человека, не состоящего в браке, при прочих равных условиях. То есть добавление фиктивной переменной в регрессию по существу позволяет оценить размер изменения зависимой переменной при наличии некоторого признака по сравнению с его отсутствием.
46
•
А. С. Малова. Основы эконометрики в среде GRETL
Здесь стоит обратить внимание на еще один важный момент. Такое свойство человека, как «состоит в браке», можно также описать другой фиктивной переменной
. Если эту
переменную включить в регрессию, то результат будет такой же, как и в случае с фиктивной переменной с точностью до знака, то есть по сравнению с человеком, состоящим в браке, человек не в браке зарабатывает на 160,7 единиц меньше.
Рис. 11.2
Поскольку две переменные и описывают одно и то же и являются абсолютно линейно-зависимыми , их нельзя вместе включать в регрессию, так как это приведет к появлению мультиколлинеарности (об этом написано подробно в главе 13). Поэтому в регрессию включается только одна из переменных, а вторая, которая не была включена, называется базовой. Если в регрессию включена переменная , то по сравнению с базовой переменной ( ) заработная плата состоящих в браке людей в среднем выше на 160,7 единиц. Аналогичная интерпретация может быть дана переменной . Интерпретация коэффициента фиктивной переменной в случае, когда зависимая переменная — логарифм В одном из предыдущих разделов мы рассмотрели интерпретацию коэффициентов регрессии в случае, когда одна из переменных (регрессоры или зависимая переменная) логарифм. Теперь рассмотрим случай, когда зависимая переменная — это логарифм, а один из регрессоров — фиктивная переменная. Рассмотрим сквозной пример про заработную
11. Фиктивные переменные (dummy variables)
•
47
плату и используем в качестве зависимой переменной не , а ее логарифм . Оценим соответствующую регрессию
[файл с данными wage2.gdt]. Оцененная регрессия будет выглядеть так:
Рис. 11.3
Интерпретация коэффициентов всех регрессоров будет одинакова — коэффициент при каждом регрессоре нужно умножить на 100%, чтобы получить приблизительную оценку эффекта от изменения регрессора при прочих равных условиях. В сравнении с людьми, не состоящими в браке, те, кто в браке состоят, зарабатывают в среднем на 17,7% больше. Однако это приблизительная оценка, она верна только в случае, если коэффициент достаточно мал. Чтобы получить точную, нужно использовать формулу . В рассматриваемом случае это . Расхождение в оценках становится заметным, когда коэффициенты при переменных достаточно велики (как в нашем случае). В ситуации, когда коэффициенты меньше 0,1, расхождение при приблизительном и точном вычислении будет незначительно. Использование фиктивных переменных для множественных категорий (порядковая информация) В предыдущих подразделах были рассмотрены ситуации, когда категорий, которые описывает фиктивная переменная, всего две: пол либо мужской, либо женский, человек либо в браке, либо нет, покупатель
48
•
А. С. Малова. Основы эконометрики в среде GRETL
оплачивает покупку наличными либо картой. Но также достаточно часто встречаются явления, в которых категорий для описания, больше, чем две. Наиболее часто приводимый пример — это сезонные переменные, которые отражают влияние времени года на зависимую переменную. Сезонов четыре, и описать их одной фиктивной переменной не удастся. В таком случае нужно создать некоторое количество переменных по количеству категорий, то есть четыре. Каждая сезонная переменная в отдельности будет фиктивной:
Эти переменные все вместе полностью описывают явление «сезон», при этом эти переменные в совокупности являются абсолютно линейно зависимыми, поэтому их нельзя все вместе включать в регрессию из-за возникновения полной мультиколлинеарности. Одна из переменных принимается за базовую и она не включается в регрессию, а остальные переменные в регрессию входят. Интерпретация переменных при включенных в регрессию фиктивных переменных соотносится с базовой переменной. Рассмотрим условную модель . В данной модели опущена переменная , то есть ее мы полагаем базовой. Интерпретация коэффициентов при остальных регрессорах будет: изменится в среднем на единиц зимой по сравнению с летом, изменится в среднем на единиц весной по сравнению с летом, изменится в среднем на единиц осенью по сравнению с летом, значение летом составит в среднем . Теперь разберем, как можно использовать знания о фиктивных переменных для описания множественных категорий при работе с моделью заработной платы. В имеющихся данных есть переменная , которая содержит в себе информацию об образовании респондента. Эта переменная была включена в регрессию в качестве количественной, при увеличении срока образования на 1 год заработная плата в среднем растет на 39,6 единиц. Переменную можно перекодировать в аналогичную переменную , которая уже будет категориальной. В новой переменной содержатся следующие значения: 1 — респондент без образования (менее 10 лет образования), 2 — школьное образование (больше или равно 10 годам, но менее 12 лет), 3 — колледж (больше или равно 12 годам, но менее 15), 4 — университетское образование (больше или равно 15 годам, но менее 17 лет), 5 — ученая степень (больше или равно 17 годам образования).
11. Фиктивные переменные (dummy variables)
•
49
Для того чтобы построить категориальную переменную , нужно выбрать пункт меню Добавить — Добавить новую переменную и после этого ввести формулу для вычисления категорий новой переменной [6]:
Это не фиктивная переменная, но нам ее исследование будет полезно, чтобы понять возможности фиктивных переменных. Добавим эту переменную в наше регрессионное уравнение вместо количественной переменной :
и оценим данное уравнение.
Рис. 11.4
Переменная , хоть формально и является порядковой, будет в данном случае интерпретироваться как категориальная, то есть при повышении уровня образования на одну ступень (при переходе от состояния «без образования» к состоянию «школьное образование», от состояния «школьное образование» к состоянию «колледж» и т. д.) в среднем заработная плата растет на 92,1 единицы. Однако из практических соображений очевидно, что прирост заработной платы при повышении образования от школьного уровня до уровня колледжа существенно меньше, чем, например, от уровня колледжа до университетского образования. В данном случае эффект от каждой дополнительной ступени образования не дифференцируется, а усредняется. Для того чтобы получить дифференцированный эффект и понять, какой вклад в заработную плату дает каждый конкретный уровень об-
50
•
А. С. Малова. Основы эконометрики в среде GRETL
разования, введем пять фиктивных переменных, которые будут в совокупности полностью описывать образование респондента:
Задание для самостоятельной работы В GRETL постройте фиктивные переменные , на основе переменной рабочий файл.
, , , и добавьте их в основной
Эти переменные в совокупности линейно зависимы, потому все вместе не могут быть включены в регрессионное уравнение либо нужно исключить из уравнения константу. Примем за базовую переменную и включим остальные переменные в регрессию:
Оценим получившееся уравнение:
Рис. 11.5
Из четырех добавленных фиктивных переменных коэффициенты при двух из них получились незначимы. После проведения теста на сов-
•
11. Фиктивные переменные (dummy variables)
местную незначимость переменные из регрессии.
и
51
были исключены
Задание для самостоятельной работы Проверьте правильность спецификации модели с использованием доступных вам методов и инструментов GRETL.
Окончательный вариант оцененной модели представлен на рис. 11.6.
Рис. 11.6
Интерпретируя результаты оценивания, можно сказать, что по сравнению с респондентами, имеющими школьное образование (напомним, что переменная была базовой переменной), те, кто имеет университетское образование, получают в среднем на 137,1 единиц больше, а те, кто имеет ученую степень, — на 191,8 единицы больше. При этом переменные и были исключены как переменные с незначимыми коэффициентами. Это можно интерпретировать следующим образом: статистически значимой разницы в заработной плате тех, кто не имеет образования, имеет только школьное образование или закончил колледж, не наблюдается. Те выводы, которые были сделаны для университетского образования и ученой степени по сравнению со школьным образованием, справедливы и при сравнении с ситуацией без образования и с колледжем. Задание для самостоятельной работы Оцените имеющуюся модель в ситуации, когда в качестве базовой переменной вы берете . Сравните результаты с теми, которые были получены ранее. Прокомментируйте их и сделайте выводы.
Взаимодействие фиктивных переменных Добавим к модели заработной платы еще одну переменную, которая будет характеризовать расу респондента
52
•
А. С. Малова. Основы эконометрики в среде GRETL
Оценим регрессию: . Результаты оценивания представлены на рис. 11.7
Рис. 11.7
Задание для самостоятельной работы Скажите, как раса влияет на заработную плату, исходя из информации, представленной на рис. 11.7.
Теперь мы хотим ответить на вопрос, влияет ли семейное положение на уровень заработной платы белых людей. Основываясь на распечатке GRETL на рис. 11.7, мы не можем ответить на этот вопрос, каждый в отдельности регрессор оказывает влияние на зависимую переменную, но совместное влияние не очевидно. Для ответа на поставленный вопрос необходимо сконструировать переменную и добавить ее в регрессию, при этом каждую фиктивную переменную ( ) по отдельности не исключать. Оценим получившееся уравнение: . После добавления нового регрессора коэффициент при перестал быть значимым. Попробуем удалить регрессор . После этого коэффициенты при всех регрессорах модели стали значимыми.
11. Фиктивные переменные (dummy variables)
•
53
Рис. 11.8
Рис. 11.9
Используя результаты оценки регрессии на рис. 11.9, можно сказать, что семейное положение влияет на уровень заработной платы представителей различных этносов. Так, женатые афроамериканцы получают в среднем на 98,7 единиц меньше, чем неженатые белокожие. Если сравнить с результатами на рис. 11.7, то можно сделать вывод, что семейный статус частично компенсирует разрыв в заработной плате между белокожими и афроамериканцами, но тем не менее дискриминация остается. Разные наклоны регрессии с использованием фиктивных переменных Вопросы о влиянии фиктивной переменной на некоторую количественную переменную также правомерны. По существу, это вопрос об угле наклона переменной. Разберемся, как влияет этнос респон-
54
•
А. С. Малова. Основы эконометрики в среде GRETL
дента на отдачу от образования, если оценивать уровень образования как количественную переменную. Создадим новую переменную и оценим регрессию .
Рис. 11.10
После добавления нового регрессора коэффициент при перестал быть значимым даже на 10%-ном уровне. Исключим его из регрессии (рис. 11.11).
Рис. 11.11
Коэффициент при значим. Положим, переменная , тогда оцененное уравнение принимает вид
.
•
11. Фиктивные переменные (dummy variables)
Если переменная
55
, то регрессия имеет вид .
Таким образом, из того, что коэффициент при регрессоре составляет 9,5, мы можем заключить, что каждый дополнительный год образования для афроамериканцев дает вклад в заработную плату на 9,5 единиц меньше, чем каждый дополнительный год образования для белокожих.
12. ТЕСТ ЧОУ (TEST CHOW) Достаточно часто при проведении эконометрических исследований требуется проверить однородность выборки, на которой строится модель, либо установить факт наличия или отсутствия структурного сдвига в данных после некоторого наблюдения. Проверка однородности выборки может быть необходима тогда, когда мы знаем, что по некоторому признаку результаты оценивания регрессии могут отличаться для той части выборки, которая этим признаком обладает, и той, которая не обладает. В сквозном примере про заработную плату таким признаком, по которому можно разделить выборку, может являться пол. Действительно, с точки зрения экономической социологии факт того, что у женщин заработная плата может зависеть от образования, опыта и проч. не так, как у мужчин, выглядит правдоподобно. Отсюда возникает необходимость проверки однородности выборки по полу, нет ли статистической разницы в значениях регрессоров и зависимой переменной для мужчин и для женщин. Примером того, что выборка, вероятно, неоднородна после некоторого наблюдения, может быть предположение о том, что после возраста 30 лет структура формирования заработной платы и ее зависимости от регрессоров меняется. Для того чтобы отвечать на эти и прочие вопросы о структуре выборке, а точнее о ее однородности или неоднородности по какому-либо признаку, существует тест Чоу (test Chow). Общая идея теста Чоу состоит в том, что выборка делится на две части: первая часть соответствует одному значению контрольного признака, вторая часть — другому (выборка делится на две части: наблюдения для мужчин и наблюдения для женщин; другой пример: первая часть — респонденты в возрасте до 30 лет включительно, вторая часть — респонденты после 30 лет). По обеим частям выборки оценивается регрессия и тестируются коэффициенты этой регрессии. Если их значения признаются статистически равными — выборка считается однородной и обе части можно объединять; если коэффициенты имеют значимое статистическое различие в оценках, выборку объединять нельзя и нужно оценивать модели на двух ее частях отдельно [2, 3, 9].
•
12. Тест Чоу (test Chow)
57
Тест Чоу (test Chow) для проверки однородности выборки позволяет ответить на вопросы о том, является ли выборка однородной по некоторому признаку, были ли в данных структурные сдвиги (изменилась ли выборка после некоторого наблюдения) и проч.
Гипотезы
не так, где — коэффициенты регрессии, оцененной по первой части выборки (от 1 до n наблюдения), а — коэффициенты регрессии, оцененной по второй части выборки (от n + 1 до n + m наблюдения)
Расчетная статистика
, — сумма где квадратов остатков для модели всей выборки (от 1 до n+m наблюдения) , сумма квадратов где остатков для модели по первой части выборки (от 1 до n наблюдения), сумма квадратов остатков модели, оцененной по второй части выборки (от n + 1 до n + m наблюдения); k — количество регрессоров модели
Правило принятия решения (гипотеза H0 отвергается, если):
где n + m— число наблюдений; k — число регрессоров в модели
Рассмотрим варианты проведения теста Чоу на примерах. Ответим на первый вопрос, одинакова ли модель формирования заработной платы для мужчин и для женщин [файл с данными wage2.gdt]. В данном случае всего у нас 935 наблюдений в выборке. Чтобы провести тест, нужно оценить для начала регрессию с ограничением, то есть в предположении, что результаты оценки для мужчин и для женщин одинаковы и выборку можно объединять. Оцененная по всей имеющейся выборке модель представлена на рис. 12.1.
58
•
А. С. Малова. Основы эконометрики в среде GRETL
Рис. 12.1
В оцененной регрессии нас интересует значение суммы квадратов остатков модели, оно составляет . После этого нам нужно найти значений суммы квадратов остатков модели без ограничений для того, чтобы посчитать F-статистику. В списке переменных у нас есть переменная «пол» (переменная , которая принимает два значения: 0 — если респондент женщина и 1 — если респондент мужчина). Для того чтобы разделить выборку на две части по переменной «пол», сначала отсортируем ее по соответствующей переменной с помощью меню Данные — Сортировать данные, сортировать по переменной .
Рис. 12.2
После этого заметим, на каком номере наблюдения заканчиваются данные для женщин и начинаются данные для мужчин. В нашем примере — это 101 наблюдение.
•
12. Тест Чоу (test Chow)
59
Рис. 12.3
Ограничим выборку на 100-м наблюдении (Выборка — Установить диапазон).
Рис. 12.4
Ограничение выборки по фиктивной переменной можно провести еще и другим способом в GRETL. Для этого в основном меню выбираем Выборка — Изменить на основе критерия и указываем критерий для ограничения выборки — для ограничения по мужчинам и — для ограничения по женщинам. После этого оценим регрессию на ограниченном диапазоне (для женщин) (рис. 12.5).
60
•
А. С. Малова. Основы эконометрики в среде GRETL
В данном случае нас интересует сумма квадратов остатков, которая составляет . Заметим, что все коэффициенты получились не значимыми. В данном случае на это не стоит обращать внимание, так как построенная регрессия является вспомогательной, то есть она нам требуется лишь для проведения теста и пока не представляет самостоятельной ценности. К этой регрессии мы вернемся чуть позже, когда проведем тест до конца.
Рис. 12.5
Теперь изменим параметры выборки, установим диапазон от 101 до 935 и оценим регрессию для второй части, то есть только по данным мужчин.
Рис. 12.6
В данном случае нас также интересует сумма квадратов остатков . Мы можем рассчитать сумму квадратов остатков для модели без ограничений (то есть модели, в которой мы оцениваем регрессии для каждой из частей выборки, предполагая их различными)
•
12. Тест Чоу (test Chow)
и
61
. Зная значения , мы можем вычислить значение F-статистики.
критическое значение
,
, нулевая
гипотеза отвергается, то есть выборку объединять нельзя, вклад регрессоров в формирование заработной платы разный для мужчин и для женщин. Теперь вспомним о том, что регрессия, оцененная по первой части выборки (то есть для женщин), была не значима, тогда как регрессия по второй части выборки была значима. Результаты теста Чоу показывают, что выборка неоднородна по полу и данные для каждого пола нужно рассматривать по отдельности.
Рис. 12.7
Тест Чоу можно также провести в автоматическом режиме. Для этого после оценки регрессии по всей выборке без деления на части (рис. 12.1) выберем в меню Тесты — Тест Чоу. В диалоговом окне выберем переменную, по которой будем тестировать на наличие сдвигов в выборке, — в нашем случае это переменная . Результаты проведения теста представлены на рис. 12.8. Значение F-статистики для теста Чоу представлено в самом низу распечатки и совпадает с тем значением, которое было получено при проведении теста вручную. Можно либо сравнить рассчитанное значение F-статистики с критическим, либо обратить внимание, что р-значение = 0,0058. Это говорит о том, что можно отвергнуть нулевую гипотезу об однородности выборки. Теперь рассмотрим вариант проведения теста Чоу для случая, когда нужно определить структурный сдвиг по некоторому наблюдению — например, проверим, что формирование заработной платы у респондентов до 30 лет включительно отличается от формирования заработной платы для респондентов старше 30 лет [файл с данными wage2.gdt].
62
•
А. С. Малова. Основы эконометрики в среде GRETL
Рис. 12.8
Значение суммы квадратов остатков модели с ограничением такое же, как и для предыдущего примера . Для того чтобы разбить выборку на две части, также отсортируем наблюдения по переменной по возрастанию (напомним, что это делается через Данные — Сортировать данные). До 251 наблюдения включительно будет первая часть выборки, с 252 наблюдения — вторая часть.
Рис. 12.9
•
12. Тест Чоу (test Chow)
63
Установим сначала диапазон выборки от 1 до 251 наблюдения, оценим регрессию и найдем , затем выставим диапазон выборки от 252 до 935 наблюдения и получим значение , таким образом, . Зная сумму квадратов остатков для регрессии с ограничением и без ограничения, рассчитаем F-статистику 1,84, , , нулевая гипотеза принимается, то есть нет различия в структуре формирования заработной платы по возрасту, выборки можно объединять. При проведении данного теста автоматически мы устанавливаем просто номер наблюдения, по которому происходит деление выборки для проверки ее однородности.
Рис. 12.10
Результаты автоматического теста приведены на рис. 12.11.
Рис. 12.11
Значение F-статистики, рассчитанное автоматически, совпадает с тем, что было получено вручную. р-значение составляет 0,076, что больше 5%-го уровня значимости, а значит, нулевая гипотеза не должна быть отвергнута, выборка однородна.
13. МУЛЬТИКОЛЛИНЕАРНОСТЬ (MULTICOLLINEARITY) Мультиколлинеарность — свойство данных, при котором регрессоры в модели оказываются полностью или частично линейно зависимы. Полная мультиколлинеарность возникает тогда, когда регрессоры связаны друг с другом некоторой функциональной зависимостью (значение одного регрессора однозначно определяется значением другого регрессора). Примером возникновения полной мультиколлинеарности может быть включение в регрессию полной группы фиктивных переменных, например переменные
и
описывают одну и ту же характеристику — пол и образуют полную группу фиктивных переменных, то есть . Если обе эти переменные включить в регрессию, то также будет иметь место полная мультиколлинеарность. Частичная, или стохастическая мультиколлинеарность возникает в ситуации, когда регрессоры стохастически линейно зависимы, по сути это означает, что прямой линейной связи между регрессорами нет, но они изменяются похожим образом. Последствиями мультиколлинеарности является то, что, с одной стороны, снижается точность оценок коэффициентов регрессии, а с другой стороны — тест Стьюдента работает некорректно и можно совершить ошибку, проверяя значимость того или иного коэффициента при регрессоре. Для того чтобы проверить наличие мультиколлинеарности, используют следующие признаки: 1. рами больше
— коэффициент корреляции между регрессо, возможна мультиколлинеарность.
2. Нужно оценить регрессию
и получить значение
,
затем оценить регрессию любого из регрессоров на остальные регрессоры
, где
, и получить
13. Мультиколлинеарность (Multicollinearity)
значение
. Если
•
65
, то возможно наличие мультиколлинеар-
ности. 3. Значение
, возможна мультиколлинеарность.
Параметр (variance inflation factor) для j-регрессора показывает, насколько увеличивается оценка стандартного отклонения для коэффициента при регрессоре по сравнению с ситуацией, если бы мультиколлинеарности не было. 4. Если регрессия значима в целом по тесту Фишера, а по тесту Стьюдента все коэффициенты не значимы, возможна мультиколлинеарность. 5. Если регрессия имеет неправильные с точки зрения теории знаки или слишком большие по модулю коэффициенты — возможна мультиколлинеарность. 6. Если незначительное изменение в данных (например, добавление или удаление малого количества наблюдений) приводит к существенному изменению коэффициентов регрессии — возможна мультиколлинеарность. В случае, если мультиколлинеарность идентифицирована, ее можно попытаться устранить несколькими способами. Наиболее простой по сути, но сложный в исполнении способ борьбы с мультиколлинеарностью — добавление новых данных для построения регрессии. Если при проведении исследования есть возможность получить дополнительные данные, то это может помочь, но, как правило, когда дело доходит до оценки регрессии, используются все данные, которые удалось собрать, и рекомендация добавить новые данные не работает. В таком случае представляется возможным попытаться исключить коррелирующие регрессоры либо наложить на них некоторые ограничения и проверить связанные с этим гипотезы. Это может помочь в устранении дублирования информации. Рассмотрим возможности проверки некоторых признаков мультиколлинеарности в GRETL. Признак № 1
— коэффициент корреляции между регрессорами больше , возможна мультиколлинеарность.
Для того чтобы построить корреляционную матрицу регрессоров [файл с данными wage2.gdt], в основном окне GRETL выбираем Вид — Корреляционная матрица.
66
•
А. С. Малова. Основы эконометрики в среде GRETL
Рис. 13.1
Если проанализировать корреляционную матрицу регрессоров (на рис. 13.1 доступна только часть матрицы), то коэффициента корреляции более нет. Здесь можно еще обратить внимание на то, что, вообще говоря, корреляция между зависимой переменной и регрессорами также невелика. Этот факт не позволяет рассчитывать на высокий в модели, однако вместе с тем модель он построить также не мешает. Признак № 2
Нужно оценить регрессию и получить значение , затем оценить регрессию любого из регрессоров на остальные регрессоры
, и получить
где значение
,
. Если
, то возможно наличие мульти-
коллинеарности.
Результаты оценки коэффициентов исходной регрессии представлены на рис. 5.4. Качество подгонки у данной модели . Возьмем произвольный регрессор и оценим вспомогательную модель. Например, в качестве псевдозависимой переменной положим регрессор . В оцененной модели , то есть , этот признак мультиколлинеарности также не подтвердился.
•
13. Мультиколлинеарность (Multicollinearity)
67
Рис. 13.2
Признак № 3
Значение
, возможна мультиколли-
(variance inflation factor) для неарность. Параметр j-регрессора показывает, насколько увеличивается оценка стандартного отклонения для коэффициента при регрессоре по сравнению с ситуацией, если бы мультиколлинеарности не было.
Исходя из результатов проверки предыдущего признака рассчитаем значение коэффициента разом получаем, что значение
. Таким об, наличие мультиколлинеарности
не подтверждается.
Коэффициент также можно рассчитывать и средствами GRETL. Для этого в окне оцененной регрессии (рис. 13.3) выбираем Тесты — Мультиколлинеарность.
68
•
А. С. Малова. Основы эконометрики в среде GRETL
Рис. 13.3
Под заголовком Метод инфляционных факторов расположены все коэффициенты для всех регрессоров уравнения. Признак № 4, признак № 5, признак № 6
•Если регрессия значима в целом по тесту Фишера, а по тесту Стьюдента все коэффициенты не значимы — возможна мультиколлинеарность. •Если регрессия имеет неправильные с точки зрения теории знаки или слишком большие по модулю коэффициенты — возможна мультиколлинеарность. •Если незначительное изменение в данных (например, добавление или удаление малого количества наблюдений) приводит к существенному изменению коэффициентов регрессии — возможна мультиколлинеарность.
Последние три признака мультиколлинеарности носят характер вспомогательных. Это значит, что если наличие первых пяти признаков не подтвердилось, то, скорее всего, остальных сигналов о наличии мультиколлинеарности также не появится, однако если хотя бы один из вспомогательных признаков присутствует — стоит провести проверку более формальными методами.
14. ГЕТЕРОСКЕДАСТИЧНОСТЬ (HETEROSCEDASTICITY) Что такое гетероскедастичность Все методы работы с регрессионным уравнением и подходы к его анализу, которые были рассмотрены до настоящего момента, совершались в предпосылке, что рассматриваемое регрессионное уравнение удовлетворяет требованиям нормальной линейной регрессионной модели. Теперь рассмотрим, что происходит, если эти предпосылки нарушаются, и как с этим справляться. Одной из наиболее часто встречающихся проблем, с которой сталкиваются те, кто занимается практическими эконометрическими исследованиями, является гетероскедастичность, или неоднородность дисперсий ошибок регрессионного уравнения (в отличие от гомоскедастичности — однородности дисперсий ошибок регрессионного уравнения). Подробнее с понятием гетероскедастичность можно ознакомиться в [7, 9]. Причины гетероскедастичности могут быть самые разнообразные, но наиболее частые — это ошибка в спецификации модели либо природа данных. Последствиями гетероскедастичности является некорректная работа тестов Стьюдента и Фишера для проверки значимости коэффициентов при отдельных регрессорах и регрессии в целом, что приводит к ошибкам в исследовании. Вообще говоря, любое регрессионное уравнение нужно проверять не только на значимость и эконометрическую адекватность, но еще и на наличие гетероскедастичности. Способы выявления гетероскедастичности будут рассмотрены ниже. Тест Уайта (White test) Наиболее простой способ выявления гетероскедастичности — тест Уайта. Он несложен технически, при этом его чувствительность достаточно высока. К его недостаткам можно отнести то, что данный тест позволяет установить факт гомоскедастичности или гетероскедастичности, но не позволяет сделать предположений о возможных способах коррекции. Гипотезы теста Уайта (постоянство дисперсий остатков, гомоскедастичность). не так (дисперсии остатков непостоянны, гетероскедастичность).
70
•
А. С. Малова. Основы эконометрики в среде GRETL
Процедура теста Уайта 1. Оцениваем регрессионное уравнение, подозрительное на наличие гетероскедастичности, и получаем остатки этого уравнения. 2. Оцениваем регрессию квадратов остатков из исходного уравнения на все регрессоры исходного уравнения, их квадраты и попарные произведения (в коротком варианте теста Уайта регрессию квадратов остатков из исходного уравнения можно оценивать только на сами регрессоры исходного уравнения, без квадратов и попарных произведений), получаем значение для этого вспомогательного уравнения. Обозначаем через p общее количество регрессоров во вспомогательном уравнении (константа тоже регрессор). 3. Сравниваем , где n — число наблюдений, — качество подгонки во вспомогательной модели, p — число регрессоров во вспомогательной модели, — значение статистики с p –1 степенью свободы на уровне значимости . Выводы теста Уайта 1. , следовательно, не отвергается, гетероскедастичность. 2. , следовательно, не отвергается, гомоскедастичность. Рассмотрим процедуру проведения теста Уайта на примере [файл с данными hprice1.gdt]. Построим зависимость цены на дом ( от общей площади участка ( , площади дома ( и числа спален в доме ( : .
Рис. 14.1
Далее нам нужно сохранить квадраты остатков оцененного регрессионного уравнения. Для этого выбираем пункт меню Сохранить-Квадраты остатков.
• 71
14. Гетероскедастичность (Heteroscedasticity)
Рис. 14.2
После того как квадраты остатков сохранены в переменной usq1, их нужно оценить на все регрессоры тестируемой модели, их квадраты и попарные произведения. Для этого создадим новые переменные: чтобы создать квадраты регрессоров, выделяем необходимые переменные и выбираем меню Добавить — Квадраты для выделенных переменных. Чтобы создать попарные произведения регрессоров, используем меню Добавить — Добавить новую переменную и в открывшемся окне вписываем формулу для новой переменной.
Рис. 14.3
После чего оцениваем необходимую нам регрессию: .
Рис. 14.4
72
•
А. С. Малова. Основы эконометрики в среде GRETL
Из полученной регрессии нас интересует только значение . Вспомним еще раз, что мы тестируем гипотезу (гомоскедастичность) против гипотезы гетероскедастичность. Расчетная статистика , критическая статистика . Учитывая, что, , гипотеза отвергается, в исходном уравнении присутствует гетероскедастичность. Аналогично процедуру теста Уайта можно провести в GRETL автоматически. Для этого после того, как исходное (тестируемое) уравнение было оценено, выбираем меню Тесты — Гетероскедастичность — Тест Вайта либо Тесты — Гетероскедастичность — Тест Вайта (только квадраты). Второй вариант теста подразумевает, что во вспомогательное уравнение будут включены только сами регрессоры и их квадраты, попарные произведения не будут в нем присутствовать. Этот вариант теста разумно использовать тогда, когда в исходном уравнении достаточно большое количество регрессоров. С точки зрения точности расхождения в стандартном и сокращенном варианте теста Уайта не значительны, поэтому использование того или иного варианта остается на усмотрение исследователя. В рассматриваемом примере регрессоров не слишком много, поэтому можно воспользоваться стандартной, а не сокращенной версией теста Уайта.
Рис. 14.5
С точностью до погрешности вычисления значение расчетной статистики, полученной через встроенный тест, совпадает с тем, которое было получено вручную. Вывод о том, чтобы отвергнуть, можно сделать как исходя из сравнения расчетной и критической статистики, так и опираясь на p-значение, которое составляет 0,0001, то есть близко к нулю, значит, можно отвергнуть нулевую гипотезу, гетероскедастичность присутствует.
•
14. Гетероскедастичность (Heteroscedasticity)
73
Задание для самостоятельной работы Проведите встроенную процедуру теста Уайта только для квадратов модели, а также проделайте тест вручную. Сравните полученные результаты.
Сильной стороной теста Уайта является его простота и удобство технической реализации (он представлен во всех эконометрических пакетах), при этом его недостатком можно считать то, что он не дает возможности распознать форму гетероскедастичности, а только установить факт ее наличия или отсутствия. С точки зрения коррекции гетероскедастичности хотелось бы также иметь представление о том, какова ее природа. Для того чтобы попытаться распознать форму гетероскедастичности, существует тест Голдфельда–Квандта. Тест Голдфельда–Квандта (Goldfeld–Quandt test) При идентификации гетероскедастичности бывает полезно установить, какую форму имеют дисперсии остатков. Это помогает более точно применять методы коррекции гетероскедастичности. Одним из тестов на наличие гетероскедастичности с возможностью установления формы дисперсий остатков является тест Голдфельда–Квандта. Так, в гипотезах теста предполагается, что дисперсия остатков зависит от некоторого регрессора и изменения в дисперсии объясняются изменениями в регрессоре. Предположим, дисперсия остатков зависит от некоторого регрессора . Гипотезы теста Голдфельда–Квандта (постоянство дисперсий остатков, гомоскедастичность). (дисперсия остатков непостоянна, гетероскедастичность; дисперсия остатков зависит от регрессора ). Процедура теста Голдфельда–Квандта 1. Сортируем наблюдения по возрастанию регрессора . 2. Делим выборку на две части, исключив около четверти наблюдений из середины (исключаем из выборки d наблюдений. В первой части выборки остается
наблюдений и во второй части выборки
остается такое же количество наблюдений). 3. Оцениваем регрессию по двум частям выборки и из каждого оцененного уравнения выписываем значение суммы квадратов остатков для модели. По первой части выборки мы получаем значение и по второй части выборки получаем значение . 4. Вычисляем значение расчетной статистики и сравниваем его со значением критической статистики . Если
гипотеза
в уравнении присутствует гетероскедастичность.
отвергается,
74
•
А. С. Малова. Основы эконометрики в среде GRETL
Выводы теста Голдфельда–Квандта 1. , следовательно, не отвергается, гетероскедастичность. 2. , следовательно, не отвергается, гомоскедастичность. Спецификации теста Голдфельда–Квандта Для данного теста также возможна альтернативная спецификация. (постоянство дисперсий остатков, гомоскедастичность). (дисперсия остатков непостоянна, гетероскедастичность; дисперсия остатков зависит от регрессора ). Вся механика теста будет такая же, как описано ранее, единственное отличие будет состоять в том, что сортировать наблюдения нужно по убыванию регрессора и расчетная статистика будет вычисляться как
.
Рассмотрим процедуру проведения теста Голдфельда–Квандта на примере. Оценим регрессию .
Рис. 14.6
Проведем встроенный тест Уайта и убедимся, что в данной модели присутствует гетероскедастичность.
Рис. 14.7
В распечатке теста р-значение = 0,00, что позволяет отвергнуть гипотезу о гомоскедастичности. Если проанализировать график зависимости
14. Гетероскедастичность (Heteroscedasticity)
•
75
остатков от переменной (это можно сделать через пункт меню Графики — Графики остатков — В зависимости от ), то можно наглядно увидеть зависимость остатков от регрессора.
Рис. 14.8
Будем тестировать гипотезу о том, что дисперсия остатков зависит от регрессора . (постоянство дисперсий остатков, гомоскедастичность). (дисперсия остатков непостоянна, гетероскедастичность; дисперсия остатков зависит от регрессора ). Отсортируем наблюдения по возрастанию переменной . Для этого в основном меню выберем Данные — Сортировать данные и переменную для сортировки выберем .
Рис. 14.9
После сортировки исключим из рассмотрения серединные наблюдения выборки. Всего в выборке 88 наблюдений, исключить нужно четверть, то есть 22 наблюдения. Выборка делится на две части — в первой части остаются наблюдения с 1 по 34, а во второй части — с 55 по 88.
76
•
А. С. Малова. Основы эконометрики в среде GRETL
Для того чтобы оценить регрессию по двум выборкам, ограничиваем диапазон через меню Выборка — Установить диапазон.
Рис. 14.10
После чего оценим регрессию по первому и по второму диапазону.
Рис. 14.11
Получаем, что
и
. Рассчитаем зна-
чение F-статистики, она составляет тическое значение
. Кри,
,
то есть гипотеза отвергается, гетероскедастичность присутствует в модели, причем форма дисперсии остатков известна.
•
14. Гетероскедастичность (Heteroscedasticity)
77
Коррекция Тест Голдфельда — Квандта позволяет не только протестировать наличие гетероскедастичности, но и выявить подходы к ее коррекции. . Чтобы дисперсия Так, например, мы установили, что остатков стала постоянна, необходимо поделить обе части на переменную янную величину
. Если оценить дисперсию мы получим постои
. Если все
регрессоры и зависимую переменную уравнения поделить на
, то
мы получим устойчивые по отношению к гетероскедастичности оценки:
. Чтобы оценить эту регрессию, созда-
дим несколько новых переменных, а именно — и
, где scal — это единичный вектор (переменная,
компоненты которой единицы). Чтобы создать scal, выбираем в основном меню Добавить — Фиктивная переменная по диапазону наблюдений.
Рис. 14.12
После этого оценим уравнение:
Рис. 14.13
.
78
•
А. С. Малова. Основы эконометрики в среде GRETL
Оцененное уравнение выглядит следующим образом: , при этом нужно помнить, что тот коэффициент, который является константой в данном уравнении, — это коэффициент наклона прямой в исходном, а угол наклона в данном уравнении — это константа исходного уравнения. При этом стандартные ошибки коэффициентов и коэффициент детерминации (в скорректированной модели они рассчитаны верно) берутся также соответственно регрессорам. Мы можем выписать исходной уравнение, оцененное с поправкой на гетероскедастичность: . Если гетероскедастичность присутствует в модели как свойство данных, то для оценки такой модели стоит использовать обобщенный метод наименьших квадратов.
15. АВТОКОРРЕЛЯЦИЯ (AUTOCORRELATION) Существует несколько типов данных: пространственные данные, временные ряды и панельные данные. Пространственные данные — это данные о некотором наборе объектов и их наблюдаемых характеристик в один и тот же момент времени; временные ряды — это наблюдения за одним и тем же объектом в последовательные моменты времени; панельные данные — это данные о наборе объектов и их характеристиках в последовательные моменты времени. До настоящего момента в данном пособии мы имели дело только с пространственными данными. Однако теперь возникла необходимость обсудить явление, которое характерно для временных рядов, — это автокорреляция. Вообще говоря, работа с временными рядами — это отдельный раздел эконометрики, освещение которого не входит в задачи этого пособия (подробнее см. [1]), однако в данном случае обойти вниманием автокорреляцию мы также не можем, поскольку одной из предпосылок линейной регрессионной модели является необходимость отсутствия автокорреляции в модели. Что такое автокорреляция и ее причины Начнем с рассмотрения авторегрессионного процесса 1-го порядка, то есть , — белый шум, процесс, который характеризуется нулевым средним и постоянной дисперсией. Автокорреляцией 1-го порядка называется явление, при котором остатки модели удовлетворяют авторегрессионному процессу 1-го порядка. Причин автокорреляции может быть много, наиболее основные из них это: 1) неправильная спецификация модели; 2) циклические преобразования данных; 3) наличие лагированных переменных. Различают два типа автокорреляции 1-го порядка: положительную и отрицательную. Положительная автокорреляция ( ) характеризуется тем, что ошибки в модели очень редко меняют знак, и наблюдения достаточно большими группами располагаются по разные стороны регрессионной прямой. Отрицательная автокорреляция ( ) типична тем, что ошибки очень часто меняют знак и наблюдения располагаются не случайным образом вокруг прямой, а через одно.
80
•
А. С. Малова. Основы эконометрики в среде GRETL
К последствиям наличия автокорреляции можно отнести то, что дисперсии ошибок занижаются, следовательно, коэффициент детерминации завышается, стандартные ошибки рассчитываются некорректно, поэтому, некорректно работают тест Стьюдента на значимость отдельных коэффициентов и тест Фишера на значимость регрессии в целом. Тест Дарбина–Ватсона (Durbin–Watson test) Требования теста Дарбина–Ватсона 1. В уравнении должна быть константа. 2. В данных не должно быть пропусков. 3. Регрессоры должны быть детерминированы. 4. В регрессии не должно быть лагированных зависимых переменных. 5. Тест Дарбина–Ватсона тестирует только автокорреляцию первого порядка. 6. Регрессоры и ошибки не должны быть коррелированны. «Приблизительный вариант» теста Дарбина–Ватсона Оценим регрессионное уравнение, подозрительное на наличие автокорреляции, сохраним остатки этого уравнения и оценим авторегрессию первого порядка для остатков: . Статистика Дарбина–Ватсона вычисляется следующим образом: . Значение коэффициента
Значение статистики DW
Вывод
Автокорреляции нет Положительная автокорреляция Отрицательная автокорреляция
Гипотезы теста Дарбина–Ватсона (автокорреляции нет). (автокорреляция есть: либо ). Процедура теста Дарбина–Ватсона 1) Оцениваем регрессионное уравнение, подозрительное на наличие автокорреляции. 2) Сохраняем остатки оцененного уравнения. 3) Оцениваем авторегрессию первого порядка на остатках: . 4) Вычисляем значение статистики Дарбина–Ватсона . 5) По таблицам критических значений определяем критические точки статистики Дарбина–Ватсона. Этих точек будет две: и . Располагаем эти точки на отрезке от 0 до 4 в следующей последовательности: [0; ; ; 4 – ;4 – ;4] и определяем, в какой из интервалов попадает расчетное значение статистики Дарбина–Ватсона.
•
15. Автокорреляция (Autocorrelation)
81
Выводы теста Дарбина–Ватсона Интервал, в который попала статистика Дарбина–Ватсона:
Положительная автокорреляция ) (
[0; ] [ ;
Невозможно сделать вывод
] ]
Отсутствие автокорреляции ( )
;4– ]
Невозможно сделать вывод
[ ;4– [4 –
Вывод:
[4 – ; 4]
Отрицательная автокорреляция ( )
Рассмотрим использование теста Дарбина–Ватсона в GRETL [файл с данными hseinv.gdt]. Оценим уравнение зависимости инвестиций в жилье от цен на жилье в логарифмах , где linvpc — логарифм реальных инвестиций в жилье (млн долларов), lprice — логарифм индекса цен на жилье (базовый период — 1982 г., данные ежегодные с 1947 по 1988 г.), и протестируем его на наличие автокорреляции. В файле hseinv.gdt данные представлены как временные ряды. Стоит заметить, что в GRETL нет возможности работать с автокорреляцией, если данные классифицируются как пространственные. Поэтому из технических соображений рассмотрим, как менять структуру данных на временные ряды. Для этого нужно выбрать в основном меню пункт Данные — Структура данных. Далее последовательно в открывающихся окнах выбираем «Временные ряды».
Рис. 15.1
Затем выбираем частоту данных (если точно не известна частота данных, можно выбрать опцию Другая).
82
•
А. С. Малова. Основы эконометрики в среде GRETL
Рис. 15.2
После чего подтверждаем, что данные нумеруются с первого наблюдения по последнее. В рассматриваем примере необходимости в изменении структуры данных нет, поэтому перейдем непосредственно к оценке уравнения.
Рис. 15.3
В принципе, после того, как мы оценили уравнение, статистика Дарбина–Ватсона уже отражена в распечатке GRETL и составляет DW = 0,81. Однако проделаем всю процедуру теста. Сохраним остатки из оцененного уравнения. Это можно сделать через Сохранить — Остатки (остатки сохранятся в переменной uhat1). После этого оцениваем регрессию . Выбираем Модель — Метод наименьших квадратов, после чего в качестве зависимой
•
15. Автокорреляция (Autocorrelation)
83
переменной ставим uhat1 и нажимаем кнопку Лаги, чтобы добавить в регрессоры первый лаг зависимой переменной.
Рис. 15.4
В результате должна получиться следующая спецификация модели.
Рис. 15.5
84
•
А. С. Малова. Основы эконометрики в среде GRETL
Оцененное уравнение представлено на рис.15.6:
Рис. 15.6
Из распечатки можно выписать значение , значение стати. стики Дарбина–Ватсона Найдем критические значения статистики Дарбина–Ватсона. Это можно сделать с использованием таблиц либо через GRETL. Для этого в основном окне выберем Инструменты — Критические значения — Дарбина–Ватсона. Установим размер выборки 41, число экзогенных переменных — 1 (не считая константу).
Рис. 15.7
Критические значения будут иметь следующий вид:
Рис. 15.8
Рассчитаем крайние точки для интервалов теста Дарбина–Ватсона и определим, в какую область попадает статистика DW = 0,84: Интервал, в который попала статистика Дарбина-Ватсона:
Вывод:
[0; 1,45]
Положительная автокорреляция (
[1,45; 1,54]
Невозможно сделать вывод
[1,54; 4 – 1,54] = [1,54; 2,46]
Отсутствие автокорреляции (
)
)
•
15. Автокорреляция (Autocorrelation)
85
Окончание табл. Интервал, в который попала статистика Дарбина-Ватсона:
Вывод:
[4 – 1,54; 4 – 1,45] = [2,46; 2,55] Невозможно сделать вывод [4 – 1,45; 4] = [2,55; 4]
Отрицательная автокорреляция (
)
Статистика попадает в интервал [0; 1,45], в рассматриваемом примере нулевая гипотеза об отсутствии автокорреляции отвергается. Существенными недостатками теста Дарбина–Ватсона является то, что он позволяет тестировать только автокорреляцию первого порядка и в нем присутствуют зоны неопределенности. Однако чем больше размер выборки, тем меньше становятся зоны неопределенности. Положительным моментом теста Дарбина–Ватсона является то, что он позволяет понять знак автокорреляции, то есть определить, положительная она или отрицательная. Встроенный тест на наличие автокорреляции До настоящего момента мы говорили об автокорреляции 1-го порядка, то есть о наличии в ошибках модели авторегрессионного процесса 1-го порядка. На практике возможно присутствие в ошибках авторегрессионного процесса более высокого порядка, то есть в случае, если ошибки модели удовлетворяют авторегрессионному процессу p-го порядка , то говорят о наличии автокорреляции p-го порядка в модели. Для тестирования автокорреляции любого порядка в GRETL предусмотрен встроенный тест. После того как мы оценили уравнение, подозрительное на наличие автокорреляции, выберем меню Тесты — Автокорреляция, установим нужный порядок лагов для тестирования (он может быть больше, чем 1, однако в данном примере нам нужно протестировать автокорреляцию 1-го порядка).
Рис. 15.9
86
•
А. С. Малова. Основы эконометрики в среде GRETL
GRETL предлагает целую серию тестов на наличие автокорреляции [тест Бреуша–Годфри (Breusch–Godfrey test), LM–тест, тест Льюнга– Бокса (Ljung–Box test)]. В приведенных тестах проверяется одна и та же гипотеза H0: автокорреляции нет против гипотезы H1: автокорреляция есть. Для того чтобы принять решение о наличии или отсутствии автокорреляции, обратим внимание на p-значения каждого из тестов. p-значения < 0,05, можно отвергнуть нулевую гипотезу, то есть автокорреляция в рассматриваемом уравнении присутствует. Коррекция Для коррекции автокорреляции можно попробовать изменить спецификацию. Если автокорреляция 1-го порядка и известен ее коэффициент , то можно проделать некоторое преобразование, а именно рассмотрим само уравнение и это же уравнение, но с лагированными переменными . После чего вычислим разность этих уравнений, предварительно умножив лагированный вариант уравнения на коэффициент , то есть . Их разность будет выглядеть как представлено далее: . В таком случае ошибки уже не будут коррелированы и можно оценивать уравнение .
Рис. 15.10
Возможен и другой вариант поправки — это встроенная в GRETL процедура, которая позволяет вычислять робастные оценки стандартных
•
15. Автокорреляция (Autocorrelation)
87
ошибок. Для этого на этапе спецификации модели нужно установить галочку в окне Робастные стандартные ошибки. Если оценить модель с указанной поправкой, то результат будет следующим:
Рис. 15.11
Стоит обратить внимание на то, что оценки коэффициентов остались неизменными, однако стандартные ошибки и, следовательно, расчетные значения статистик были скорректированы.
16. LOGIT- И PROBIT-МОДЕЛИ До настоящего момента мы рассматривали модели, в которых зависимая переменная была количественной, бинарная переменная (или фиктивная переменная) выступала только в качестве регрессора. Бывают ситуации, в которых необходимо отвечать не на «количественный» вопрос (например, как зависит объем спроса на товар от его цены), а на «качественный», например, вернет человек вовремя кредит или нет, поступит школьник в университет или нет, купит семья автомобиль или нет. Для ответов на подобные вопросы в качестве зависимой переменной в регрессионном уравнении используется бинарная переменная и для оценивания таких уравнений применяются logit- и probit-модели [2, 3, 9]. В общем случае необходимо оценить вероятность наступления события. Так, например, если мы принимаем за единицу факт поступления школьника в университет (у = 1), а за ноль факт непоступления (у = 0), то в качестве зависимой переменной в модели будет вероятность поступления школьника в университет . Основной идеей как logit-, так и probit-модели является оценивание вероятности наступления события через функцию, область значений которой лежит в диапазоне [0,1]: . Наиболее часто в качестве функции используют функцию стандартного нормального распределения и функцию логистического распределения. Logitмодель где Probitмодель где
Logit-модель: оценивание и прогнозирование Рассмотрим модель оценки вероятности одобрения кредита [файл с данными loanapp.gdt]. Для оценки logit-модели выбираем меню Модель — ограниченная зависимая переменная — Логит–Бинарный.
• 89
16. Logit- и probit-модели
Рис. 16.1
Для начала выпишем уравнение регрессии по распечатке GRETL для logit-модели:
. Чтобы построить прогноз вероятности одобрения кредита при некоторых известных значениях регрессии, нужно подставить эти значения в оцененное уравнение и вычислить значение логистической функции. Например, если мы хотим узнать вероятность выдачи кредита белому заявителю, у которого 20% расходов на коммунальные платежи и 13% прочих расходов, то мы вычислим
. Прогноз также можно построить и в GRETL (аналогично тому, как строился прогноз для линейной модели). Для этого добавляем одно новое наблюдение (Данные — Добавить новое наблюдение), затем для регрессоров, участвующих в регрессии, добавляем значения в это последнее новое наблюдение ( ), после чего оцениваем уравнение регрессии (оно автоматически будет оценено по исходному диапазону, так как в зависимой переменной нет значений нового наблюдения) и выбираем в меню Анализ — Прогнозы:
90
•
А. С. Малова. Основы эконометрики в среде GRETL
Рис. 16.2
Прогнозное значение представлено на рис. 16.3.
Рис. 16.3
Также можно оценить logit-модель и построить прогноз вероятности для заданных значений регрессоров c использованием скриптов в GRETL [5, 6]. Скрипт GRETL можно написать и запустить через меню основного окна Файл — Скрипты — Новый скрипт — Скрипт для GRETL. В открывшемся окне сначала нужно записать функцию, которая позволит оценить требуемую logit-модель, а затем еще одну функцию, позволя-
•
16. Logit- и probit-модели
91
ющую рассчитать прогнозное значение вероятности для оцененной модели при заданных значениях регрессоров:
Рис. 16.4
Для того чтобы запустить скрипт, нужно нажать на значок, изображающий две шестеренки. После запуска программа выдаст следующий результат:
Рис. 16.5
На рисунке 16.5 представлена сначала распечатка оценки logit-модели (та же, которую мы получили, использовав меню Модель — Модели с ограниченными зависимыми переменными — Logit), а следом прогнозное значение вероятности одобрения кредита при заданных значениях регрессоров, которое составляет 97,2%. Probit-модель: оценивание и прогнозирование Аналогично logit-модели можно оценить и probit-модель через Модель — Ограниченная зависимая переменная — Пробит — Бинарный.
92
•
А. С. Малова. Основы эконометрики в среде GRETL
Рис. 16.6
Чтобы вычислить прогнозное значение вероятности одобрения кредита белому заявителю, у которого 20% расходов на коммунальные платежи и 13% прочих расходов, необходимо рассчитать
. Прогнозное значение вероятности для probit-модели также можно вычислить через скрипт в GRETL. Запускаем Файл — Скрипты — Новый скрипт — Скрипт для GRETL. В открывшемся окне нужно записать для начала команду оценки probit-модели ( ), а затем функцию, которая генерирует значения нормального распределения для заданного аргумента. Эта функция имеет синтаксис , где N — это постоянный аргумент, дающий понять, что нужно вычислять значение стандартного нормального распределения, а — это значение, от которого нужно вычислить значение функции нормального распределеможно ния. При этом в качестве значения аргумента ( записать как конкретное число, так и линейную функцию. Проведем расчет с помощью подобного скрипта на нашем примере для таких же значений регрессоров, как мы считали в случае logit-модели, то есть . Скрипт будет выглядеть как представлено ниже:
• 93
16. Logit- и probit-модели
Рис. 16.7
Результатом работы скрипта будет следующая распечатка:
Рис. 16.8
Исходя из распечатки, вероятность одобрения кредита при заданных параметрах составляет 97,5%. Очень часто возникает потребность расчета прогнозного значения для средних значений регрессоров. Это можно сделать также через скрипт:
.
Рис. 16.9
94
•
А. С. Малова. Основы эконометрики в среде GRETL
Результаты вычисления представлены на рис. 16.10. Аналогично можно посчитать вероятность одобрения кредита при средних значениях регрессоров и для logit-модели.
Рис. 16.10
Проверка значимости коэффициентов регрессии и оценка качества регрессии Значимость отдельных коэффициентов при регрессорах в бинарных моделях (как logit, так и probit) можно проверять, ориентируясь либо на р-значения, либо сравнивая расчетные значения статистики с критическими значениями для нормального распределения, а не с критическими значениями распределения Стьюдента. Нужно обратить внимание на то, что р-значения выводятся в распечатке не по умолчанию. Для этого нужно при оценке регрессии выбрать соответствующую опцию либо после того, как модель оценена, выбрать Правка — Изменить модель и также выбрать нужную опцию. Для проверки гипотез о коэффициентах модели используется тест отношения правдоподобия, в частности он позволяет проверять гипотезу о совместной незначимости коэффициентов модели.
• 95
16. Logit- и probit-модели
Рис. 16.11
Тест отношения правдоподобия позволяет проверить линейные гипотезы о коэффициентах в модели. Частным случаем такой проверки является проверка коэффициентов при регрессорах на совместную незначимость. Правило принятия Гипотезы Расчетная статистика решения (гипотеза отвергается, если): линейные ограничения верны не так
, где q — количество где — функция линейных правдоподобия для модели с ограничениями; ограничений — функция правдоподобия для модели без ограничений; q — количество линейных ограничений
Проиллюстрируем данный тест примером. Добавим в исходную модель несколько новых регрессоров так, чтобы она приняла вид
96
•
А. С. Малова. Основы эконометрики в среде GRETL
где: loanamt — сумма кредита, appinc — доход заявителя, и оценим ее с использованием логистической функции (для probit-модели процедура тестирования аналогична):
Рис. 16.12
Мы видим, что два коэффициента в данной модели не значимы и поэтому требуется проверка на их совместную незначимость для того, чтобы понять, можно ли их исключить совместно или нужно один из регрессоров оставить. Значение функции правдоподобия для данной модели (это модель без ограничения) . Оценим теперь модель с ограничением, то есть исключим регрессоры с подозрительными на совместную незначимость коэффициентами:
Рис. 16.13
• 97
16. Logit- и probit-модели
Для тестирования избыточных переменных в автоматическом режиме можно использовать тест Вальда (как и для обычной регрессионной модели). Для этого в окне модели выбираем Тесты — Избыточные переменные — Тест Вальда, переносим регрессоры с подозрительными на незначимость коэффициентами в поле для тестирования.
Рис. 16.14
Результат тестирования, представленный на рис. 16.15, показывает, что коэффициенты являются совместно незначимыми (p-значение = 0,14 > 0,05, гипотеза H0 принимается) и могут быть исключены из регрессии:
Рис. 16.15
Для оценки качества модели используется аналог — это . Коэффициент детерминации McFadden вычисляется как , где
— это значение функции правдоподобия для оценива-
емой модели, а — значение функции правдоподобия для модели, которая включает в себя только константу. Если максимум правдоподобия для полной модели близок к значению максимума правдоподобия для модели только с константой (то есть их частное близко к единице),
98
•
А. С. Малова. Основы эконометрики в среде GRETL
то объясняющая способность модели будет близка к нулю. В рассматриваемом примере для logit-модели , для probit-модели — практически такой же и составляет , что в обоих случаях свидетельствует о не очень высокой объясняющей способности моделей. Также достаточно часто для оценки качества модели бинарного выбора используют число корректно предсказанных значений, в данном случае для logit-модели процент корректно предсказанных случаев составляет 88%, для probit-модели — 87,9%. Этот показатель не всегда является приемлемым, так как в случае, если в наблюдаемых значениях зависимой переменной имеется смещение в сторону одного из вариантов (допустим, единиц существенно больше в наблюдениях, чем нулей), то даже если модель не точна и в качестве расчетных значений зависимой переменной мы будем получать только единицы (как результат округления расчетной вероятности в ту или иную сторону по правилам округления), процент корректно предсказанных значений будет в любом случае велик. Интерпретация коэффициентов Теперь рассмотрим, как интерпретировать оценки для коэффициентов регрессионного уравнения. Поскольку наблюдается нелинейная зависимость, то очевидно, что эффект от изменения одного регрессора при прочих равных условиях не будет постоянным, а будет изменяться. В общем виде эффект от изменения i-го регрессора можно выписать следующим образом: изводная функции,
, где
— первая про-
— значение коэффициента при i-м регрессоре.
Logitмодель
Probitмодель
Для того, чтобы оценить эффект от изменения одного регрессора, необходимо также знать значения остальных регрессоров. На базовом уровне считают среднее значение для каждого из регрессоров и при заданном среднем вычисляют предельный эффект от изменения отдельно взятого регрессора, но для более точного прогноза стоит считать предельный эффект для конкретных интересующих значений регрессоров (не средних значений).
•
16. Logit- и probit-модели
99
Интерпретация коэффициентов: logit-модель На практике предельный эффект от изменения некоторого регрессора проще считать через скрипты в GRETL. Оценим, как изменится вероятность одобрения кредита при повышении доли расходов на коммунальные услуги на 1% при том, что исходные траты на коммунальные услуги составляют 20%, прочие расходы составляют 13% и заемщик белый. Для этого напишем скрипт:
Рис. 16.16
Результат оценивания представлен на рис. 16.17:
Рис. 16.17
При изменении доли расходов заемщика на коммунальные услуги на 1% вероятность одобрения кредита вырастет на 0,0006% (результат расчета предельного эффекта представлен внизу распечатки).
100
•
А. С. Малова. Основы эконометрики в среде GRETL
Для logit-моделей помимо оценки предельного эффекта от изменения регрессоров также существует и другая интерпретация коэффициентов, а именно — число е, возведенное в степень, равную коэффициенту перед регрессором, показывает изменение шансов на реализацию события, в данном случае на получение кредита, при изменении регрессора на единицу. При этом число показывает исходные шансы на реализацию события при заданных условиях. Чем отличаются шансы от вероятности? Если шанс получить одобрение кредита составляет, к примеру,
— то есть четыре одобрения приходятся на один отказ
в кредите (из пяти заемщиков один получает отказ и четверо получают одобрение), то есть, вероятность одобрения кредита составляет
.
Мы можем вычислить шансы и их изменения, также используя инструмент скриптов. Для вычисления шансов запишем:
Рис. 16.18
Результат выполнения скрипта:
Рис. 16.19
• 101
16. Logit- и probit-модели
Чтобы оценить, как изменятся шансы получения кредита при росте, например, доли расходов на коммунальные услуги на 1%, запустим следующий скрипт:
Рис. 16.20
Результат исполнения скрипта представлен ниже:
Рис. 16.21
При росте расходов на коммунальные услуги на 1% шансы одобрения кредита вырастут в 1,02 раза. Интерпретация коэффициентов: probit-модель Для probit-модели вычисления также могут быть произведены с использованием возможностей скриптов GRETL, а именно через функцию pdf можно вычислить плотность распределения в заданной точке и далее умножить значение плотности на коэффициент при соответствующей переменной. Синтаксис функции pdf аналогичен синтаксису функции cdf, то есть , где N — это постоянный аргумент, дающий понять, что нужно вычислять значение плотности стандартного нормального распределения,
102
•
А. С. Малова. Основы эконометрики в среде GRETL
а — это значение, от которого нужно вычислить само значение плотности нормального распределения. Для того чтобы узнать, каков предельный эффект от изменения доли коммунальных расходов на 1% для белого заемщика при исходных коммунальных расходах в размере 20% и прочих расходах в размере 13%, запишем скрипт:
:
Рис. 16.22
Результаты вычисления представлены на рис. 16.23.
Рис. 16.23
Для белого заемщика, имеющего 20% коммунальных и 13% прочих расходов, при увеличении доли коммунальных расходов в бюджете на 1% вероятность одобрения кредита возрастает на 0,0007%.
17. СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ При моделировании экономических ситуаций достаточно часто возникает проблема невозможности полного описания взаимодействия величин и объектов через единственное регрессионное уравнение. Так, например, спрос на некоторый товар среди прочего определяется ценой на этот товар. Вместе с тем очевидно также, что цена товара некоторым образом зависит от спроса. Возникает необходимость построения нескольких регрессионных уравнений, причем задача осложняется тем, что, как в примере со спросом и ценой, та переменная, которая в одном из уравнений была экзогенной (внешней, влияющей переменной), в другом уравнении становится эндогенной (внутренней, зависимой переменной). Совокупность такого рода уравнений носит название систем одновременных уравнений [1, 9]. Такие уравнения достаточно часто требуют специальных методов оценки, так как МНК оценки не являются состоятельными. Разберем некоторые основы работы с системами одновременных уравнений на примере. Рассмотрим пример с данными, определяющими статус занятости замужних женщин в США [файл с данными mroz.gdt]. Составим следующую систему одновременных уравнений: , где первое уравнение отражает занятость замужних женщин, причем — это объем занятости замужних женщин в часах, — логарифм заработной платы женщины, — доход семьи работающей женщины, — количество детей младше 6 лет в семье. Второе уравнение моделирует объем заработной платы работающей женщины, все переменные, входящие в него, уже обозначены, кроме — это уровень образования женщины в годах. Поскольку в данном случае количество часов занятости в неделю и заработная плата работающей замужней женщины одновременно зависят друг от друга, переменные и являются эндогенными, тогда как остальные переменные в системе являются экзогенными. Совокупность указанных уравнений называется системой одновременных уравнений в структурной форме. Эндогенные переменные в системе одновременных уравнений характеризуются тем, что в каждом уравнении они коррелированы с ошиб-
104
•
А. С. Малова. Основы эконометрики в среде GRETL
кой регрессии, из-за чего непосредственное применение к каждому уравнению системы МНК приводит к смещенным и несостоятельным оценкам коэффициентов структурной формы. Оценка приведенной формы системы Приведенная форма системы одновременных уравнений позволяет выразить каждую эндогенную переменную только через экзогенные переменные, без включения в число регрессоров других эндогенных переменных. В случае системы уравнений для работающих замужних женщин приведенная форма будет выглядеть следующим образом:
Поскольку все регрессоры являются экзогенными переменными, к каждому из уравнений приведенной формы можно применить метод наименьших квадратов. Это можно сделать либо через стандартное меню GRETL Модель — Метод наименьших квадратов и оценить каждое уравнение в отдельности либо через скрипт. Поскольку мы уже знакомы со скриптами, используем их для оценивания:
Команда ols запускает выполнение метода наименьших квадратов. Та переменная, которая стоит первой, после команды ols распознается как зависимая переменная, остальные переменные, которые следуют за зависимой, считаются регрессорами.
Рис. 17.1
Результат оценивания обоих уравнений представлен на рис. 17.2. Оценки коэффициентов приведенной формы могут быть использованы для восстановления коэффициентов структурной формы. При этом возможны три принципиальные ситуации: 1) коэффициенты структурной формы могут быть однозначно выражены через коэффициенты приведенной формы (система уравнений в таком случае называется точно идентифицируемой); 2) коэффициенты структурной формы неоднозначно восстанавливаются по коэффициентам приведенной формы (система сверхидентифицируема);
•
17. Системы одновременных уравнений
105
3) коэффициенты структурной формы не могут быть восстановлены по коэффициентам приведенной формы (система уравнений называется неидентифицируемой). Процедура оценки приведенной формы и восстановления по ней коэффициентов структурной формы носит название косвенного метода наименьших квадратов.
Рис. 17.2
Оценка структурной формы системы Структурная форма системы одновременных уравнений оценивается двухшаговым методом наименьших квадратов (2МНК). В двухшаговом методе наименьших квадратов все экзогенные переменные выступают в качестве инструментальных переменных, причем одни и те же переменные выступают в качестве инструментов к обоим уравнениям системы. Запишем скрипт, необходимый для оценки системы с помощью 2МНК:
Команда tsls запускает процедуру двухшагового метода наименьших квадратов аналогично методу наименьших квадратов, первая пере-
106
•
А. С. Малова. Основы эконометрики в среде GRETL
менная после команды tsls — это зависимая переменная, остальные переменные до точки с запятой — это регрессоры. После точки с запятой указываются инструментальные переменные, по существу, все экзогенные переменные. При этом нужно учитывать, что константа тоже инструмент.
Рис. 17.3
Результаты оценивания представлены в распечатке на рис. 17.4: При оценке каждого из уравнений системы с помощью 2МНК помимо результатов оценки коэффициентов структурной формы в распечатке приводятся также результаты некоторых вспомогательных тестов: теста Хаусмана, теста на слабые инструменты (слабыми инструментами являются те переменные, которые слабо коррелируют с эндогенными переменными) и теста Саргана (проверяется допустимость использования инструментов в условиях сверхидентифицируемости).
•
17. Системы одновременных уравнений
107
Рис. 17.4
Тест Хаусмана позволяет оценить, была ли необходимость использования 2МНК (то есть являются ли оценки коэффициентов по МНК не состоятельными) Правило принятия решения (гипотеза отвергается, если):
Гипотезы МНК оценки состоятельны не так
где
р-значение — зафиксированный уровень значимости
При оценке обоих уравнений мы установили, что использование двухшагового метода наименьших квадратов оправдано, инструменты сильные. Тест Саргана для второго уравнения не проводился, так как оно не сверхидентифицируемо. По результатам оценки можно выписать оба уравнения в структурной форме:
Существует еще один способ оценивания системы уравнений в GRETL. Для этого в основном окне нужно выбрать Модель — Система уравнений. Синтаксис в этом случае также несколько напоминает скрипты. Чтобы оценить систему, нужно записать:
108
•
А. С. Малова. Основы эконометрики в среде GRETL
После чего внизу окна выбрать метод оценивания. В нашем случае это двухшаговый метод наименьших квадратов (tsls).
Рис. 17.5
Результат оценивания при этом может визуально отличаться от того, который был получен через скрипты (хотя содержательно это одни и те же уравнения и коэффициенты одинаковые) (рис. 17.6).
Рис. 17.6
Существует также еще один полезный способ оценивания системы одновременных уравнений. Случается, что есть необходимость оценить
•
17. Системы одновременных уравнений
109
каждое уравнение системы по отдельности. Для этого нужно воспользоваться меню Модель — Инструментальные переменные — Двухшаговый МНК. В открывшемся окне, так же как и для стандартного метода наименьших квадратов, выбираем зависимую переменную уравнения, регрессоры. Далее двухшаговый МНК требует выбрать инструменты (рис. 17.7).
Рис. 17.7
После этого запускаем процедуру оценки и получаем распечатку оцененного уравнения такую же, как была получена через скрипты для второго уравнения всей системы.
Рис. 17.8
110
•
А. С. Малова. Основы эконометрики в среде GRETL
Здесь стоит осветить еще один вопрос. Если двухшаговый метод наименьших квадратов достаточно хорош, почему все же лучше использовать МНК в тех случаях, когда он дает состоятельные оценки и не использовать 2МНК? При использовании МНК в случае состоятельности оценки получаются более эффективными, чем при использовании 2МНК (хотя и в этом случае оценки состоятельны).
СПИСОК ЛИТЕРАТУРЫ 1. 2. 3. 4. 5. 6. 7. 8. 9.
Вербик М. Путеводитель по современной эконометрике. М.: Научная книга, 2008. Доугерти К. Введение в эконометрику. М.: Инфра-М, 2010. Магнус Я. Р., Катышев П. К., Пересецкий А. А. Эконометрика. М.: ДЕЛО, 2004. Носко В. П. Эконометрика: в 2 т. М.: ДЕЛО, 2011. Adkins L. C. Using GRETL for Principles of Econometrics. 4th ed. 2014. Cottrell A., Lucchetti R. J. GRETL User’s Guide. 2015. Gujarati Damodar N. Basic Econometrics. 5th ed. MacGraw-Hill, 2009. Hill R. C., Griffiths W. E. Lim G. C. Principles of Econometrics. 4th ed, Wiley, 2011. Wooldridge J. M. Introductory Econometrics: A Modern Approach. 4th ed. South-Western CENGAGE Learning, 2009.
ПО И ФАЙЛЫ С ДАННЫМИ Эконометрический пакет GRETL можно скачать и установить, перейдя по ссылкам: •версия для ОС Windows http://GRETL.sourceforge.net/win32/ •версия для Mac OS http://GRETL.sourceforge.net/osx.html Все использованные в методическом пособии файлы были взяты из учебника Jeffrey M. Wooldridge «Introductory Econometrics: A Modern Approach» (2nd ed.) и доступны по ссылке: http://GRETL.sourceforge.net/GRETL_data.html 1. 2. 3. 4. 5. 6.
Wage1.gdt Wage2.gdt Hprice1.gdt Hseinv.gdt Loanapp.gdt Mroz.gdt
СОДЕРЖАНИЕ Введение……….. …………………………………………………………………………………….3 1. Линейная регрессионная модель ………………………………………………………5 2. Оценка линейной регрессионной модели ………………………………………….6 3. Тест Фишера (Fisher test)…………………………………………………………………..9 4. Тест Стьюдента (t-test) …………………………………………………………………… 12 5. Проверка гипотезы о совместной незначимости коэффициентов ……… 20 6. Проверка правильности спецификации модели (RESET test)……………. 25 7. Проверка качества регрессионной модели (коэффициент детерминации), информационные критерии …………….. 29 8. Интерпретация коэффициентов регрессии и прогнозирование ………… 33 9. Оценка регрессии в логарифмах и интерпретация ……………………………. 37 10. Проверка линейных ограничений на коэффициенты регрессии ……….. 40 11. Фиктивные переменные (dummy variables)………………………………………. 44 12. Тест Чоу (test Chow) ………………………………………………………………………. 56 13. Мультиколлинеарность (Multicollinearity) ……………………………………….. 64 14. Гетероскедастичность (Heteroscedasticity) ………………………………………… 69 15. Автокорреляция (Autocorrelation) …………………………………………………… 79 16. Logit- и probit-модели ……………………………………………………………………. 88 17. Системы одновременных уравнений …………………………………………….. 103 Список литературы …………………………………………………………………………… 111 ПО и файлы с данными …………………………………………………………………….. 111
- Оценивание нормальности распределения остатков модели
- Оценивание однородности дисперсии остатков модели. Проверка гетероскедастичности. Тест Уайта
- Функции автокорреляции и частной автокорреляции
- Периодограмма и спектр процессов
- Проверка единичных корней
- Эконометрические модели сезонных колебаний
- Авторегрессионные модели AR(p)
- Модели ARMA (p, q)
- Модели ARIMA (p, d, q)
- Метод X-12-ARIMA
- Оценивание параметров модели методом наименьших квадратов
- Верификация модели
- Тест автокорреляции Дарбина—Уотсона
- Тест автокорреляции Бройша-Годфри
- Тест автокорреляции Лджунга-Бокса
GRETL (GNU Regression, Econometrics and Time-series Library — Библиотека для регрессий, эконометрики и временных рядов) — прикладной программный пакет (ППП) для эконометрического моделирования.
GRETL является программным обеспечением, лицензия которого разрешает легально и бесплатно копировать как исходный, так и конечный код, а также самостоятельно модифицировать исходный код.
Согласно правилам FreeSoftwareFoundation, ввиду бесплатного лицензирования пакета программ на него не распространяются гарантии действующего законодательства. Относительно качества и точности функционирования пакета программ рискует только его пользователь. Однако применение пакета программ GRETL оказывается привлекательным благодаря многочисленным положительным рецензиям, публикуемым в различных экономстрических изданиях.
Основные сведения о пакете программ GRETL можно найти в Интернете на сайте http://gretl.sourceforge.net
Начало работы в GRETL
В начале работы с пакетом программ GRETL необходимо, в первую очередь, создать или открыть набор статистических данных. Каждый набор данных должен иметь один из трех типов: срезы данных (определяемые как undated), не привязанные к моментам времени; временные ряды с фиксацией периодичности наблюдений (годовые, квартальные, ежемесячные, еженедельные, ежедневные и почасовые); панельные данные — срезово-временные.
Новый набор данных создается средствами пакета программ GRETL при помощи функции File/Createdataset, объявляющей один из представленных ниже типов данных
Построение набора данных в виде временного ряда (англ. time—series) начинается с вписывания начального (например, 1990:01) и конечного (например, 2003:12) моментов, а также выбора названия первой базовой переменной.
Ручной ввод информации с клавиатуры — достаточно трудоемкое занятие, поскольку данные в каждой ячейке должны редактироваться отдельно.
Гораздо проще создавать базу фактических (не генерируемых) данных путем, импорта из заранее подготовленной таблицы EXCEL или из текстового файла, но не путем ввода данных непосредственно с клавиатуры. Импортировать можно только данные в формате xls (Excel не выше 2003)
В расчетах были использованы данные по индексу потребительских цен в зависимости от ряда экономических данных.
Файл EXCEL должен быть подготовлен следующим образом. В первой строке должны описываться переменные процессы, а в столбцах — приводиться числовые данные. В считываемой таблице EXCEL не должно храниться никаких данных помимо поименованных столбцов, поскольку отсутствие заголовка — названия столбца — приведет к некорректному импорту данных.
Источник: Куфель Т. Эконометрика: решение задач с применением пакета программ GRETL. Монография, Варшава, 2007, 200 с.

Министерство образования и науки Украины Севастопольский национальный технический университет
РЕАЛИЗАЦИЯ ЭКОНОМЕТРИЧЕСКИХ МЕТОДОВ ОБРАБОТКИ ФИНАНСОВО-ЭКОНОМИЧЕСКОЙ
ИНФОРМАЦИИ В GRETL 1.7.1
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к лабораторному практикуму
по дисциплине «Эконометрия»
для студентов специальности 6.050201 — «Менеджмент организаций» всех форм обучения
МАТЕРИАЛЫ ДОСТУПНЫ НА САЙТЕ https://sites.google.com/site/ekonometriya2014/
И В ФОРМАТЕ ВИДЕОЛЕКЦИЙ НА КАНАЛЕ youtube https://www.youtube.com/watch?v=wmyt6dFzVNM&list=PLT44QhlIFnVx
7XQCIlJnpefO_Qq6EtqHn
Севастополь
2008
2
УДК 658
«Реализация эконометрических методов обработки финансово-экономической информации в GRETL 1.7.1»
методические указания к выполнению лабораторных работ по дисциплине «Эконометрия» для студентов специальности 8.050201 – «Менеджмент организаций» всех форм обучения / Сост. А.В. Цуканов, Т.А. Кокодей. – Севастополь: Изд-во СевНТУ, 2008г. – 135 с.
Целью методических указаний является получение практических навыков построения эконометрических моделей при изучении экономических явлений и процессов с использованием системы Gretl 1.7.1.
Методические указания утверждены на заседании кафедры менеджмента и экономико-математических методов, (протокол № 5 от 23.01.2008 г.).
Допущено учебно-методическим центром СевНТУ в качестве методических указаний.
Рецензент:
Фисун С.Н., канд. техн. наук, доцент кафедры «Кибернетика и вычислительная техника».
3
СОДЕРЖАНИЕ
Лабораторная работа №1. Введение в пакет программ GRETL 1.7.1………… 5
1.Цель работы……………………………………………………………………………… 5
2.Теоретический раздел……………………………………………………………… 5
2.1.Общие сведения о пакете Gretl………………………………………………….. 5
2.2.Стартовый экран Gretl…….……………………………………………………… 6
2.3.Построение набора статистических данных………………………………………… 7
2.3.1.Ручной ввод информации с клавиатуры……………………………………… 8
2.3.2.Импорт данных…………………………………………………………………. 10
2.4.Открытие встроенного или ранее созданного набора данных………………… 11 2.5 Редактирование набора статистических данных…………………………………….. 12 2.6. Экспорт данных………………………………………………………………….. 15
3.Порядок выполнения лабораторной работы…………………………………….. 16
4.Содержание отчета о выполнении лабораторной работы………………………. 17 Библиографический список………………………………………………………….. 18
Лабораторная работа №2. Линейный регрессионный анализ взаимосвязи статистических данных в среде GRETL 1.7.1……………………………………………. 19
1.Цель работы………………………………………………………………………… 19
2.Теоретические сведения о линейном регрессионном анализе…………………….. 19
3.Описание средств системы Gretl для выполнения регрессионного анализа……………………………………………………………….……………….. 21
3.1.Оценка параметров линейной регрессионной модели методом 1МНК (OLS)
и проверка адекватности модели……………………………………………………. 21
3.2.Анализ выполнения предпосылок 1МНК…….………………………………… 28
4.Порядок выполнения лабораторной работы ……………………………………….. 33
5.Содержание отчёта о выполнении лабораторной работы…………………………. 33
Библиографический список…..………………………………………………………. 34
Приложение А. (справочное) Основные описательные статистики………………. 35 Приложение Б. (справочное) Статистические таблицы в GRETL…………………. 36 Приложение В. (справочное) Построение графиков………………………………….. 38
|
Лабораторная работа №3. Применение GRETL 1.7.1. при построении и |
40 |
|
анализе регрессионных моделей с гетероскедастичной случайной |
|
|
составляющей………………………………………………………………………… |
|
|
1. Цель работы…………………………………………………………………………… |
40 |
2. Теоретические сведения …………………………………………..………………. 40 3. Описание средств системы Gretl для выполнения регрессионного анализа при 43 наличии гетероскедастичности………………………………………………………
3.1.Пример обнаружения гетероскедастичности в Gretl ………………………….. 43
3.2.Оценивание гетероскедастичной модели с использованием взвешенного
метода наименьших квадратов ВМНК (WLS)……………………………………… 50
4.Порядок выполнения лабораторной работы ……….……………………………. 59
5.Содержание отчёта о выполнении лабораторной работы………………………….. 59
Библиографический список………………………………………………………….. 60
4
Лабораторная работа №4. Реализация метода главных компонент в среде 61
GRETL 1.7.1…………………………………………………………………………..
1.Цель работы………………………………………………………………………… 61
2.Теоретический раздел ………………………………………………………………………………. 61
|
3. Пример практической реализации метода главных компонент с |
62 |
|
использованием системы Gretl………………………………………………….…… |
|
|
3.1. Исходная информация……………………………………………………………. 63 |
|
|
3.2.Построение главных компонент и интерпретация результатов |
68 |
|
моделирования………………………………………………………………………… |
4.Порядок выполнения лабораторной работы ……….……………………………. 74
5.Содержание отчёта о выполнении лабораторной работы………………………….. 76
Библиографический список…..……………………………………………………… 77
Приложение А. (справочное) Основные показатели результатов деятельности компаний Ford Motor Company и General Motors (2002-2006)……………………… 78
Лабораторная работа №5. Анализ временных рядов в среде Gretl 1.7.1.……. 82
1.Цель работы………………………………………………………………………… 82
2. Теоретический раздел ………………………………………….……………………. 82
2.1.Анализ тренда………………………………………………………………………. 83
2.2.Декомпозиция временного ряда..……………………………………………….. 85
2.3.Анализ сезонности. Коррелограмма……………………………………………. 86
2.4.Метод авторегрессии……………………………………………………………….. 87
2.5.Спектральный (Фурье) анализ…………………………………………………. 87 3. Описание средств анализа временных рядов системы Gretl……………………. 88
3.1.Пример построение полиномиальной модели тренда…………………………. 88
3.2.Пример декомпозиции динамики макроэкономических показателей…………… 95
|
3.3. Пример анализа сезонности с применением коррелограммы ………………… |
102 |
|
3.4. Пример применения метода авторегрессии……………………………………. |
104 |
|
3.5. Пример применения метода спектрального (Фурье) анализа………………… |
107 |
4.Порядок выполнения лабораторной работы ……………………………………….. 109
5.Содержание отчёта о выполнении лабораторной работы……………………….. 110
Библиографический список…..……………………………………………………… 111
|
Приложение А. (справочное) Исходные данные……………………………………………….. |
112 |
|
Лабораторная работа №6 Анализ систем одновременных |
|
|
эконометрических уравнений в среде Gretl 1.7.1………………………………… |
115 |
1.Цель работы………………………………………………………………………… 115
2.Теоретический раздел…………………………………………..……………………. 115
3.Описание средств анализа систем одновременных эконометрических
уравнений пакета Gretl………………………………………………….………………… 117
4.Порядок выполнения лабораторной работы ……………………………………….. 128
5.Содержание отчёта о выполнении лабораторной работы………………………….. 134
Библиографический список…..……………………………………………………… 135
5
ЛАБОРАТОРНАЯ РАБОТА №1 ВВЕДЕНИЕ В ПАКЕТ ПРОГРАММ GRETL 1.7.1
1. ЦЕЛЬ РАБОТЫ
Целью данной работы является ознакомление с функциональными возможностями программного продукта Gretl 1.7.1.
2. ТЕОРЕТИЧЕСКИЙ РАЗДЕЛ
2.1. Общие сведения о пакете GRETL
Пакет программ GRETL (GNU Regression Econometrics and Time Series Library) представляет собой инструментарий для практической реализации сложных вычислительных процедур эконометрического моделирования. В 2002 году его автор проф. Аллен Котрелл (США) включил GRETL в проект www.sourceforget.net, делая его общедоступным, бесплатным продуктом с возможностью дальнейшей доработки открытых кодов (Open Source – свободным программным обеспечением). Таким образом, данный пакет программ, статистические данные для обработки, учебное пособие и исходный код всех выпущенных версий доступны на Интернет-сайтах http://gretl.sourceforge.net или http://www.kufel.torun.pl.
Возможности программы:
1.Основные описательные статистики (среднее арифметическое, медиана, минимальное и максимальное значения, среднеквадратическое отклонение, коэффициент изменчивости (вариации), коэффициент асимметрии, коэффициент эксцесса).
2.Проверка нормальности распределения, распределение частот случайной величины, распределение плотности вероятностей, определение коэффициентов корреляции и т.д.
3.Предусматривает непосредственный доступ к статистическим таблицам. Пакет Gretl содержит встроенные статистические таблицы для следующих распределений: нормального, t-распределения Стьюдента, F-распределения Фишера, хи-квадрат, Пуассона, биномиального и распределения ДарбинаУотсона. Существует возможность вычисления критических значений, p-value.
4.Анализ временных рядов (набор методов оценивания обобщённым МНК, модели ARMAX и GARCH , система уравнений авторегрессии (VAR), проверка коинтеграции; построение линии тренда, коррелограммы, периодограммы; проверка единичных корней, моделирование типа ARIMA, а также процедуры десезонализации X-12-ARIMA и TRAMO).
5.Регрессионный анализ (одношаговый метод наименьших квадратов (1МНК), взвешенный МНК, двухшаговый МНК — оценка систем одновременных уравнений, методы оценивания логитовых, пробитовых и тобитовых моделей и нелинейных моделей, и т.д.)
6
6. Метод главных компонент.
7. Экспорт и импорт GretlMicrosoft Excel и текстовые редакторы (Notepad и т.д).
8. Построение графиков и др.
Запуск программы осуществляется через Пуск-Программы-Gretl-Gretl или двойным щелчком мыши по иконке Gretl на рабочем столе.
2.2. Стартовый экран Gretl
Стартовый экран пакета программ GRETL (рисунок 1) подразделяется на три части:
—Меню, из которого реализуется набор функций. Меню функций состоит из следующих разделов: File (файл), Tools (инструменты), Data (данные),View (вид), Add (добавить), Sample (выборка), Variable (переменная), Model (модель), Help (помощь). Каждый раздел содержит группу программных функций.
—Список переменных (процессов), который содержит перечень названий и описаний переменных открытого набора данных.
—Набор иконок (пронумерованный от 1 до 10), обеспечивает быстрый
доступ к выбранным программным функциям. Набор иконок №1-10, рисунок 1.
обеспечивает быстрый доступ к некоторым программным функциям: 1. Открывает окно системного калькулятора.
2. Открывает новое окно для скриптов GRETL.
3. Открывает окно инструкций GRETL.
4. Открывает окно иконок.
5. Обращается к сайту пакета программ GRETL. 6. Открывает окно «Руководство» в pdf формате. 7. Открывает окно помощи.
8. Открывает окно определения графика разброса точек.
9. Открывает окно спецификации модели для оценивания с применением МНК.
10.Открывает окно с примерами – базы фактических данных.

7
Меню
Список переменных
Набор иконок
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Рисунок 1 — Стартовый экран GRETL
2.3.Построение набора статистических данных
Вначале работы с пакетом GRETL необходимо создать или открыть набор статистических данных. Меню File содержит команды по созданию, открытию и сохранению файлов с данными и командами GRETL.
Каждый набор данных должен иметь один из трёх типов:
1. Срезы данных (cross-sectional) – это неупорядоченный набор данных, например, данные, относящиеся к одному моменту времени и дающие нечто вроде поперечного среза: данные опроса семей об их уровнях дохода на определённый момент времени или данные о курсе доллара в различных городах на какую-то фиксированную дату (таблица 1);
2. Временные ряды (time series) – это наблюдения некоторых показателей с фиксацией периодичности (год, месяц), например, курс доллара за несколько дней (таблица 2);
3. Панельные данные (panel) – срезово-временные — это наблюдения за одной и той же группой объектов (фирмы, индивиды и т.п.), проведённые через определённые промежутки времени, т.е. это набор срезов (данные среза в динамике). Это могут быть данные ежегодных опросов выбранной группы семей об их уровнях дохода или ежеквартальный набор сведений (о прибыли, доходе и т.д.) об избранной группе фирм (таблица 3).
Таблица 1 — Данные типа срез данных (cross-sectional)
Курс доллара на 9.02.2008 по регионам
|
Севастополь |
1 |
|
Ялта |
6 |
|
Одесса |
7 |
|
Киев |
23 |
|
Львов |
45 |

8
Таблица 2 — Данные типа временной ряд (time series)
|
Курс доллара в г. Киев |
|
|
07.02.2008 |
4,9 |
|
08.02.2008 |
5 |
|
09.02.2008 |
5,06 |
Таблица 3 — Панельные данные (panel)
Панельные данные
|
07.02.2008 |
08.02.2008 |
09.02.2008 |
|
|
Киев |
4,9 |
5 |
5,06 |
|
Севастополь |
5 |
5,1 |
5,08 |
|
Одесса |
4,8 |
5,02 |
5,03 |
2.3.1. Ручной ввод информации с клавиатуры
Для создания нового набора данных необходимо выбрать пункт New Data Set в меню File (рисунок 1), указав число наблюдений создаваемого ряда (number of observations), один из перечисленных выше типов данных, и название первой создаваемой переменной набора, рисунок 2.
Сохранение данных в формате Gretl *.gdt осуществляется при помощи
FileSave Data, а закрытие набора данных при помощи FileClear Dataset.
Пример 1. В меню File выберем пункт New Data Set и введём непосредственно с клавиатуры:
Шаг 1. Число наблюдений (number of observations): «5» и нажмём кнопку «ок» (рисунок 2).
Шаг 2. Тип данных (structure of dataset): выберем срез данных (cross-sectional) и
кнопку «forward».
Шаг 3. Нажмём кнопки “ок” для подтверждения структуры данных. Шаг 4. Нажмём кнопку «yes» для подтверждения ввода данных в Gretl.
Шаг 5. Введём название переменной «А» в открывшемся окне и нажмём кнопку “ок”.
Шаг 6. В окне редактирования данных введём с клавиатуры пять значений наблюдений 1, 6, 7, 23, 45 (рисунок 3), нажмём кнопки Apply и Close, чтобы записать данную переменную в список стартового экрана (в создаваемый набор данных).
При помощи FileSave Data сохраним данный набор данных как файл example1.gdt. Закроем созданный набор данных при помощи FileClear Dataset.

9
|
ШАГ 1. |
ШАГ 2. |
ШАГ 3. |
||
|
ШАГ 6. |
ШАГ 5. |
ШАГ 4. |
||
Рисунок 2 — Этапы построения набора данных «срез данных»
Рисунок 3 — Ввод с клавиатуры данных типа «срез данных»

10
2.3.2. Импорт данных
Также возможен импорт заранее подготовленной таблицы EXСEL при помощи команды FileOpen DataImportExcel, а также некоторых других типов файлов.
Пример 2.
Осуществим импорт данных из файла Exel в пакет GRETL:
1.Создадим и поместим на рабочий стол файл example2.xls (рисунок 4).
2.Обратимся к команде Gretl — FileOpen DataImportExcel, укажем номер строки и столбца начала таблицы Excel и выберем тип данных, например, срез данных (crosssectional).
3.Дважды щёлкнем левой кнопкой мыши по названию появившихся в списке переменных стартового экрана Gretl переменных X1 и X2 для просмотра их значений (рисунок 5).
4.Сохраним набор данных FileSave Data как файл example2.gdt на рабочем столе.
Рисунок 4 — Файл с данными example2.xls
Рисунок 5 — Вывод значений импортированной переменной X1