Статья расскажет о происхождении термина «Алгоритм» и о том, какими свойствами он обладает.
Алгоритмом называют определенную конечную последовательность действий (набор инструкций), выполнение которых приводит к достижению конкретной цели (решению поставленной задачи). В литературе по информатике, как и на просторах глобальной сети, можно найти множество общей теоретической информации относительно понятия и решения алгоритма. Достаточно запомнить основную мысль: достижение алгоритмического результата обеспечивается выполнением определенной последовательности действий (чаще всего, действий арифметических или логических).
История возникновения термина
Сегодня это понятие является фундаментальным и в математике, и в информатике. Однако сам термин возник задолго до появления компьютеров и прочих электронных средств вычислительной техники. Впервые об алгоритме заговорили в средние века — именно тогда европейские ученые ознакомились с методами вычисления арифметических действий, производимых в десятичной системе счисления азиатским математиком по имени Мухаммед ибн Муса аль-Хорезми (от имени этого математика и сформировался термин Algorithm). Сочинение аль-Хорезми перевели, а в последующие столетия появилось много трудов, посвященных вопросу обучения искусству счёта посредством цифр. Можно вспомнить описание алгоритма в европейской науке в те годы:
Также значение слова «алгоритм» сегодня нередко связывают со значениями таких слов, как «рецепт», «метод», «процесс», «инструкция».
Исполнитель и программа
Судя по историческим справкам, изначально речь шла о способе выполнения арифметических действий над десятичными числами. Прошли годы. Понятие стали применять при обозначении любой последовательности действий, которая приводит к получению требуемого результата. Причем алгоритмы существуют не сами по себе — они предназначаются для конкретного исполнителя. Кто может выступать таким исполнителем:
— человек;
— роботизированное/автоматизированное устройство, механизм;
— компьютер;
— язык программирования и т. д.
Отличительная черта исполнителя — способность выполнять команды, которые включены в алгоритм. Это становится возможным, благодаря описанию последнего на формальном языке, который исключает неоднозначность толкования. Множество команд задано изначально строго и является конечным. Действия, которые должен выполнить исполнитель, называют элементарными действиями, а сама запись алгоритмической последовательности на формальном языке — это программа. Разработка алгоритма в целях решения задачи — это алгоритмизация.
Главные характеристики
Выделяют следующие свойства алгоритма: массовость, дискретность, результативность, определенность, понятность, формальность, завершаемость. Будет не лишним рассмотреть их более подробно, дав каждому свойству алгоритма пояснение:
1. Массовость (универсальность). Благодаря этому свойству, алгоритм можно успешно применять к различным наборам исходных данных. Пусть существует запись некой абстрактной последовательности, выраженная формулой. Подставляя в эту формулу значения (каждый раз новые), пользователь будет получать верные решения в соответствии с определенным алгоритмом действий.
2. Дискретность (разрывность). Это свойство характеризует структуру. Каждая алгоритмическая последовательность действий делится на этапы (шаги), а процесс решения задачи — это последовательное исполнение простых шагов. Также дискретность обозначает, что для выполнения каждого этапа потребуется конечный временной отрезок (исходные данные преобразуются во времени в результат дискретно).
3. Определенность (точность, детерминированность) — это свойство указывает алгоритму, что каждый его шаг должен быть строго определенным, то есть различные толкования должны быть исключены. Строго определяется и порядок выполнения шагов. В результате каждый шаг определяется состоянием системы однозначно, когда четко понятно, какая команда станет выполняться на следующем шаге. Как итог — при любом исполнителе для одних и тех же исходных данных при выполнении одной и той же цепочки команд будет выдаваться одинаковый результат. Да, существуют вероятностные алгоритмы — в них на последующий шаг влияют как текущее состояние системы, так и генерируемое случайное число. Но при включении способа генерации рандомных чисел в перечень «исходных данных», вероятностный алгоритм превращается в подвид обычного.
4. Понятность. Должны быть включены лишь те команды, которые доступны и понятны исполнителю, то есть входят в систему его команд.
5. Формальность. Любой исполнитель действует формально и лишь выполняет инструкции, не вникая в смысл. Он не отвлекается от поставленной задачи и не рассуждает, зачем и почему они нужны. Рассуждениями занимается разработчик алгоритма, задача же исполнителя — просто исполнить предложенные команды и получить результат. «Приказы не обсуждают, а выполняют».
6. Завершаемость (конечность). Если исходные данные заданы корректно, алгоритм завершит свое действие и выдаст результат за конечное число шагов.
7. Результативность. Согласно этому свойству, любой алгоритм должен завершаться конкретными результатами.
Основные виды алгоритмов
В информатике и программировании выделяют много видов алгоритмов. Основные из них:
— линейные (команды выполняются последовательно, одна за одной);
— разветвляющиеся (есть условие, при проверке которого возможно разветвление на несколько параллельных ветвей);
— циклические (предусматривается многократное повторение одних и тех же действий).
Источники:
• https://math-it.petrsu.ru/users/semenova/Informatika/DOC/Sam_Izuch/Algoritm.pdf;
• https://www.sites.google.com/site/algoritmyvidyisvojstva/materialy/materialy-1.
#статьи
- 7 дек 2022
-
0
Что такое алгоритмы и какими они бывают
Ты можешь разрабатывать микросервисы и знать все уровни модели OSI, но какой ты программист, если не можешь объяснить ребёнку, что такое алгоритм?
Иллюстрация: Катя Павловская для Skillbox Media
Пишет об истории IT, разработке и советской кибернетике. Знает Python, JavaScript и немного C++, но предпочитает писать на русском.
Ведущий бэкенд-разработчик мобильного приложения «Альфа-Банка».
Иногда совсем простые вопросы о профессии вводят в ступор даже опытных специалистов. Примерно так происходит, когда у разработчика с 5–10-летним стажем спрашивают: «Что такое алгоритм?»
Но для того мы здесь и собрались, чтобы дать понятные ответы на «глупые» вопросы. В этой статье расскажем, что такое алгоритмы, для чего они нужны и какими бывают.
Вы узнаете:
- Что такое алгоритмы
- Для чего их используют
- Какие у них есть свойства
- Что такое псевдокод
- Что такое блок-схемы и как их рисовать
- Примеры линейных, ветвящихся, циклических и рекурсивных алгоритмов и блок-схем
В широком смысле алгоритм — это последовательность действий, которые нужно выполнить, чтобы получить определённый результат.
Слово «алгоритм» произошло от имени персидского математика Абу Абдуллаха аль-Хорезми. В своём труде «Китаб аль-джебр валь-мукабала» учёный впервые дал описание десятичной системы счисления. А наука алгебра получила своё название в честь его книги.
Мы часто пользуемся алгоритмами в повседневной жизни. Например, когда хотим приготовить кофе в капсульной кофемашине, руководствуемся примерно таким алгоритмом:
1. Устанавливаем капсулу.
2. Проверяем уровень воды в специальном отсеке.
3. Если воды недостаточно — доливаем.
4. Ставим чашку под кран кофемашины.
5. Запускаем кофемашину.
6. Выключаем кофемашину, когда чашка наполнилась.
7. Достаём кружку.
Если не перепутать порядок шагов, то с помощью такой инструкции любой сможет порадовать себя чашкой горячего кофе. Достаточно лишь знать, как установить капсулу и включить/выключить кофемашину.
С компьютерами намного сложнее. Им неизвестно, что значит «установить капсулу», «долить воду», «запустить кофемашину» и так далее. Чтобы запрограммировать робота-баристу под определённую модель бытовой техники, алгоритм придётся расписать более детально:
1. Возьми штепсельную вилку шнура питания кофемашины.
2. Вставь штепсельную вилку в розетку.
3. Проверь, есть ли вода в отсеке для воды.
4. Если воды недостаточно:
4.1. Подними крышку отсека.
4.2. Возьми кувшин с водой.
4.3. Лей воду из кувшина в отсек, пока он не заполнится.
4.4. Закрой крышку отсека.
4.5. Поставь кувшин с водой на стол.
5. Открой крышку кофемашины.
6. Возьми из коробки капсулу с кофе.
7. Вставь капсулу в отсек для капсулы.
8. Закрой крышку кофемашины.
9. Поверни рычаг кофемашины вправо.
10. Когда чашка наполнится, поверни рычаг кофемашины влево.
11. Возьми кружку.
12. Принеси кружку хозяину.
Конечно, если мы собираем робота с нуля, то даже такой детализации будет недостаточно. Каждую процедуру ещё нужно будет реализовать на языке программирования (например, на C++ или Python), что само по себе — нетривиальная задача. Тем не менее описание стало более точным и формальным.
C научной точки зрения определение алгоритма, которое мы дали выше, не совсем точное. Ведь не всякую последовательность действий, приводящую к результату, можно назвать алгоритмом.
Алгоритм в информатике — это понятный исполнителю набор правил для решения конкретного множества задач, который получает входные данные и возвращает результат за конечное время.
У алгоритмов есть два замечательных качества: они позволяют эффективно решать задачи и не изобретать решения, которые кто-то уже придумал до нас. Это справедливо как для повседневной жизни, так и для IT.
Представьте, что оформляете загранпаспорт. Если будете всё делать сами и без инструкции, около 40 минут потратите только на выяснение необходимых справок и порядка оформления. Куда проще воспользоваться «Госуслугами», потому что алгоритм там уже составлен — делаете, что вам говорят, и ждёте результат. А ещё проще — обратиться к посреднику, который подготовит все справки и оформит паспорт за неделю.
Это очень бытовой пример, но программирование примерно так и работает. Разработчики изучают алгоритмы, чтобы писать быстрый и эффективный код, — распознают типовую задачу и подбирают для неё оптимальный алгоритм.
Допустим, нужно отсортировать в порядке возрастания числа в списке из 1000 элементов. Можно пройтись по списку 1000 раз: на каждой итерации находить наименьшее число и переставлять его в начало списка. В этом случае общее количество шагов будет равно 1 000 000 — современный компьютер справится с этим за секунду.
А если нужно упорядочить массив из 10 000 000 элементов? Тогда компьютеру придётся выполнить 1014 шагов, что потребует гораздо больше времени. Надо оптимизировать!
Разработчик, не сведущий в computer science, начнёт ломать голову над более эффективным решением. А опытный специалист применит алгоритм быстрой сортировки, который в среднем случае даст «время» 16 × 107 шагов.
Знатоки скажут, что ещё проще было бы воспользоваться библиотечной функцией сортировки (например, sorted() в Python). Тем не менее даже встроенные алгоритмы бывают недостаточно эффективными и разработчикам приходится писать собственные функции для сортировки. Но это уже совсем другая история 🙂
Теперь представьте: вы живёте в XX веке где-нибудь в США и зарабатываете тем, что ездите по городам и продаёте мультимиксеры. Чтобы сэкономить время и деньги, вам нужно придумать кратчайший маршрут, который позволит заехать в каждый город хотя бы один раз и вернуться обратно.
Это знаменитая задача коммивояжёра, для которой практически невозможно подобрать лучшее решение. Простой перебор здесь не поможет. Уже при 10 городах количество возможных маршрутов будет равно 3,6 млн, а при 26 — даже самым мощным компьютерам понадобится несколько миллиардов лет, чтобы перебрать все варианты.
Тем не менее каждый день миллионы устройств решают эту задачу: смартфоны строят маршруты между городами, а маршрутизаторы рассчитывают оптимальный путь для пакетов в сети. Дело в том, что существуют специальные алгоритмы, которые дают неидеальный, но достаточно эффективный результат. И их нужно знать, если вы хотите работать в компаниях, которые создают сложные, интересные проекты.
Информатик и автор классических учебников по программированию Дональд Кнут выделял следующие свойства алгоритмов:
- конечность,
- определённость,
- наличие ввода,
- наличие вывода, или результативность,
- универсальность,
- эффективность.
Рассмотрим каждое подробно.
Конечность. Алгоритм должен решать задачу за конечное число шагов. Необходимость этого критерия очевидна: программа, которая решает задачу бесконечно долго, никогда не приведёт к результату.
Определённость. Исполнитель (компьютер, операционная система) должен однозначно и верно интерпретировать каждый шаг алгоритма.
Наличие ввода. Как и у математической функции, результат работы алгоритма зависит от входных данных. Например, на вход алгоритма сортировки подаётся массив чисел. А функция, рассчитывающая факториал, принимает натуральное число.
Наличие вывода, или результативность. Алгоритм должен выдавать конкретный результат. Например, если мы ищем подстроку в строке и такая подстрока в ней присутствует, то на выходе мы должны получить позицию этой строки. Если такой подстроки нет — алгоритм должен вернуть соответствующее значение, например -1.
Универсальность. Алгоритм должен решать задачи с разными входными данными. Например, хорошая функция для сортировки массивов должна одинаково хорошо справляться с массивами из 10, 100 и 1 000 000 элементов.
Эффективность. Это требование продиктовано ограниченными ресурсами компьютеров. На заре развития вычислительной техники каждая секунда работы процессора, каждый байт памяти были на счету. И хотя современные компьютеры гораздо мощнее своих предшественников, они тоже могут «тормозить» из-за неэффективных алгоритмов.
Представьте, что вы изучили какой-нибудь язык программирования, например Go, и устроились бэкенд-разработчиком в IT-компанию. В вашей команде, помимо бэкендеров, есть фронтенд-разработчики, которые пишут код на JavaScript.
Вы придумали крутой алгоритм, который ускорит работу приложения, и хотите рассказать о нём коллегам. Но как это сделать, если они программируют на другом языке?
Для таких ситуаций есть псевдокод. Он позволяет изложить логику программы с помощью понятных для всех команд, не углубляясь в детали реализации конкретного языка. В учебной литературе алгоритмы описывают в основном с помощью псевдокода.
У псевдокода нет общепринятых стандартов, и авторы используют собственные оригинальные нотации. Хотя часто они заимствуют названия операций из Python, Pascal и Java. Например, код ниже напоминает программу на Python:
int linear_search(int[] arr, int x): if arr is empty: return -1 for i in 0..n: if arr[i] == x: return i return -1
Также псевдокод можно писать на русском языке, как в школьных учебниках по информатике:
ФУНКЦИЯ линейный_поиск(целое[] массив, целое x):
ЕСЛИ массив ПУСТОЙ:
ВЕРНУТЬ -1
ДЛЯ i В ДИАПАЗОНЕ ОТ 0 ДО ДЛИНА(массив):
ЕСЛИ массив[x] РАВНО x:
ВЕРНУТЬ i
ВЕРНУТЬ -1
Главное — чтобы тот, кто читает ваш алгоритм, понял его и воспроизвёл на своём языке программирования.
Если у вас в школе были уроки по информатике, то вы наверняка рисовали и читали блок-схемы. Если нет, то знайте: алгоритмы можно описывать не только словесно, но и графически.
Блок-схемы — это геометрические фигуры, соединённые между собой стрелками. Овалы, прямоугольники, ромбы и другие фигуры обозначают отдельные шаги алгоритма, а стрелки указывают направление потока данных. При этом в каждый блок записывается команда в виде логического или математического выражения.
В таблице ниже представлены основные элементы блок-схем:
Графическое изображение
Значение
Элемент кода в Python
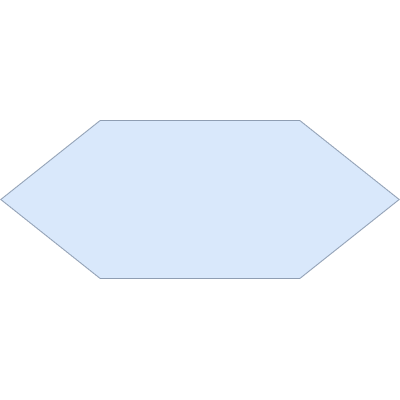
Начало/конец программы
Никак не обозначается
или обозначается как начало функции:
def foo(x): #код
Конец функции обозначается словом return
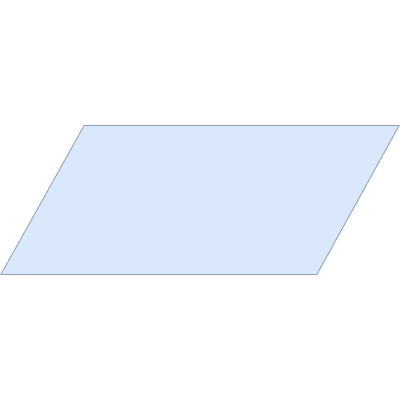
Ввод/вывод данных
Операторы ввода и вывода:
print("Hello!")
word = input()
Арифметические операции
Арифметические операторы:
100 - 10 25 + 100 6 * 12.0
Условие
Условный оператор:
if n < 5: sum += 10
Цикл со счётчиком
Цикл for:
for k,v in enumerate(arr): print(k, v)
Ввод/вывод в файл
Функции для работы с файлами:
f = open("text.txt", 'r') f.close()
С помощью этого нехитрого набора фигур можно нарисовать схему практически любого алгоритма. Другие фигуры блок-схем вы найдёте в документации к ГОСТ 19.701-90.
Блок-схемы можно рисовать в Microsoft Visio и в Google Docs (Вставка → Рисунок → Новый +). Также есть специальные сервисы: например, облачный Draw.io и десктопные Dia и yEd.
А теперь разберёмся, какими бывают алгоритмы, напишем примеры на Python и нарисуем для них блок-схемы.
По конструкции алгоритмы можно разделить на несколько групп.
В линейных алгоритмах действия идут последовательно, одно за другим. Такие программы — самые простые, но на практике они встречаются редко.
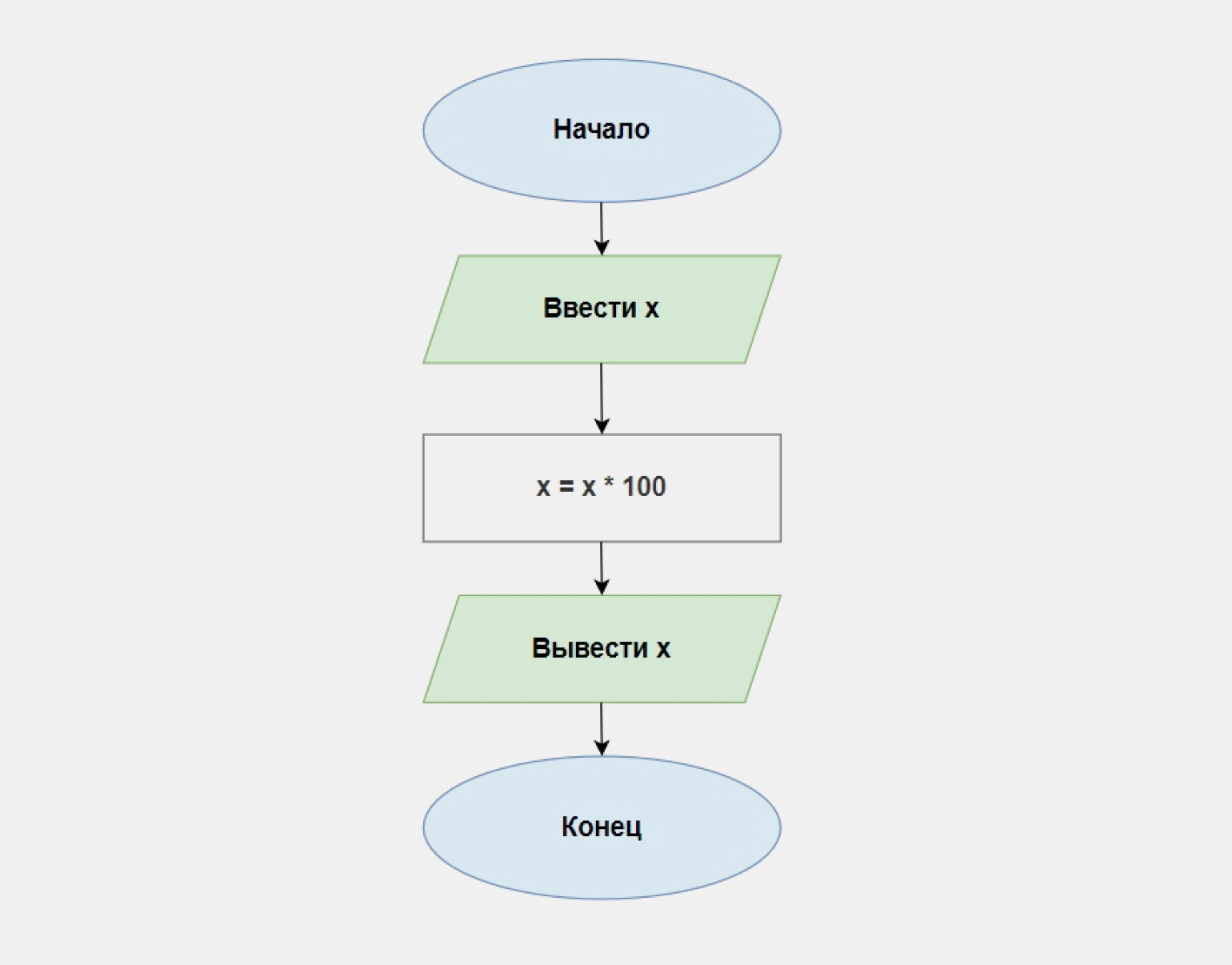
Пример. Напишите программу, которая умножает число, введённое пользователем, на 100 и выводит результат на экран.
Последовательность действий уже изложена в задании: ввести число → умножить на 100 → вывести результат. Переведём это на язык блок-схем:
Ниже приведена реализация алгоритма на языке Python:
x = int(input()) x = x * 100 print(x) >>> 5 >>> 500
В ветвящихся алгоритмах ход программы зависит от значения логического выражения в блоке «Условие». По большому счёту, любое логическое выражение сводится к выбору между истиной (True, «1») или ложью (False, «0»).
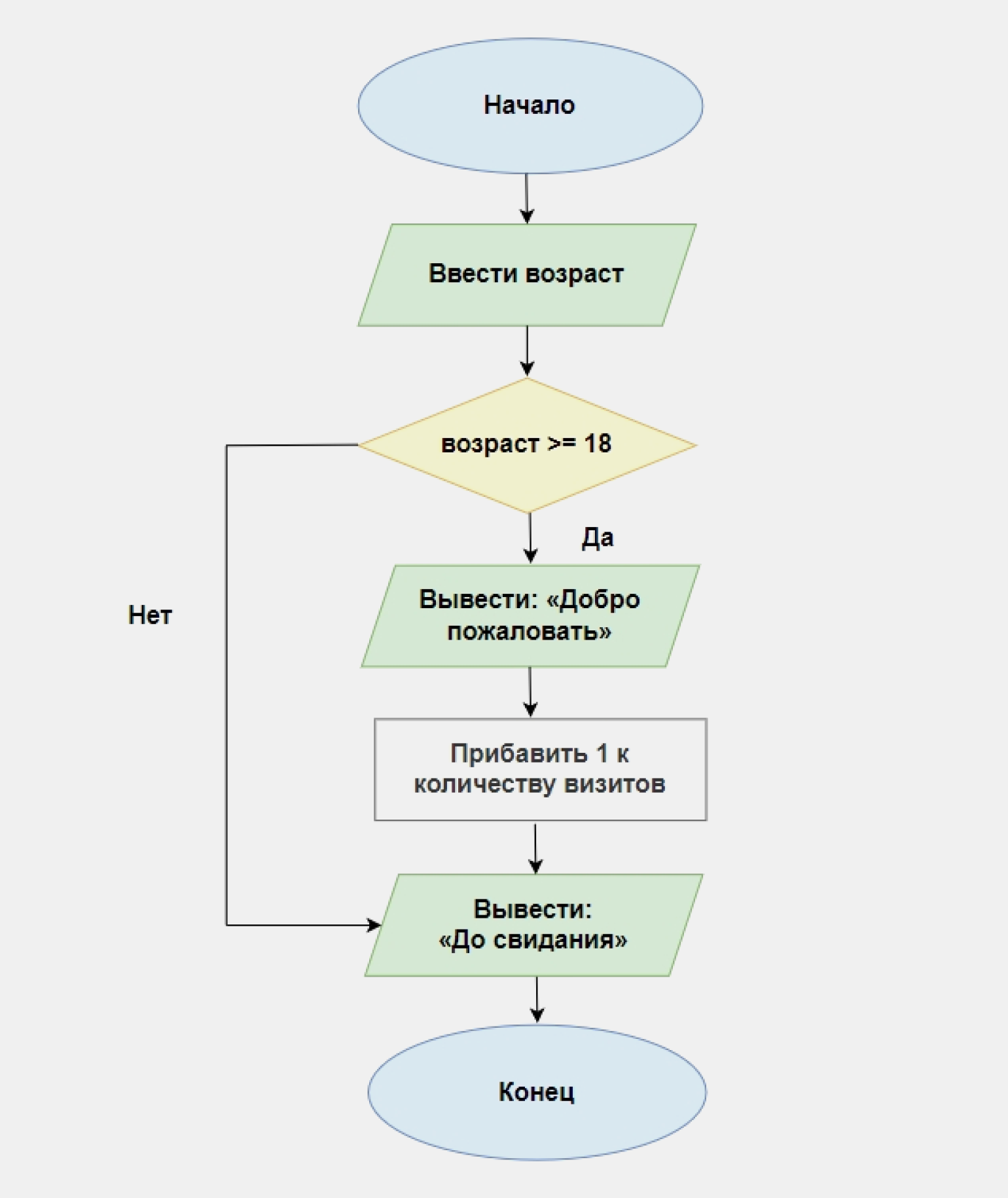
Пример. Напишите программу, которая запрашивает у пользователя возраст. Если он равен или больше 18, программа выводит приветствие, увеличивает значения счётчика посетителей на 1 и прощается, а если меньше — сразу прощается и завершает работу.
Чтобы изобразить ход решения, воспользуемся условным блоком. Во всех схемах его обозначают ромбом с вписанным условием:
То же самое на Python:
visits_counter = 0 answer = int(input("Сколько вам лет? ")) if answer >= 18: print("Добро пожаловать!") visits_counter += 1 else: print("Доступ запрещён")
Когда пользователь вводит 18 или больше, программа выполняет часть кода, которая записана под оператором if. Если же возраст меньше 18, то на экран выводится сообщение «Доступ запрещён» и программа завершает работу.
Такие алгоритмы содержат циклы — наборы действий, которые выполняются несколько раз. Количество повторений может задаваться целым числом или условием. В некоторых случаях, например, в операционных системах и прошивках микроконтроллеров, используются бесконечные циклы.
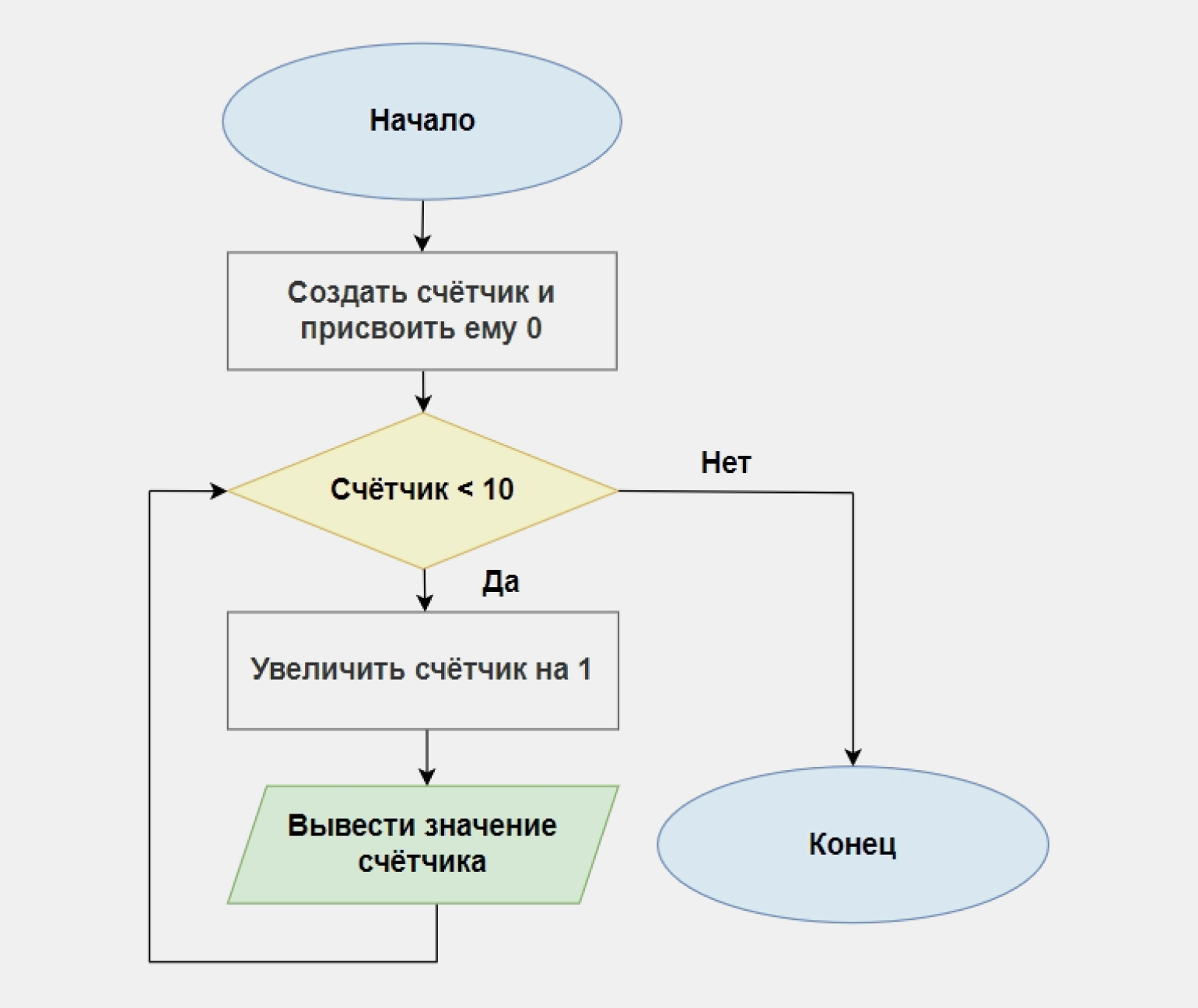
Пример. Напишите программу, которая циклично увеличивает значения счётчика на 1 и на каждом шаге выводит его значение. Когда значение счётчика достигнет 10, программа должна завершиться.
В основе нашего решения будет лежать следующее условие: если значение счётчика меньше 10 — прибавить 1, иначе — завершить работу. Вот как это выглядит в виде блок-схемы:
Переведём это в код на Python. Обратите внимание, что мы не прописываем отдельную ветвь для случая «Нет»:
count = 0 #прибавлять 1 к count, пока count меньше 10 while count < 10: count += 1 print(count) print("Переменная count равна 10!")
Результат работы программы:
1 2 3 4 5 6 7 8 9 10
Рекурсия — это явление, при котором система вызывает саму себя, но с другими входными данными. Такие алгоритмы используют для обхода словарей в глубину, вычисления факториала, расчёта степеней и других практических задач. В целом всё это можно сделать с помощью циклов, но код рекурсивных функций более лаконичен и удобочитаем.
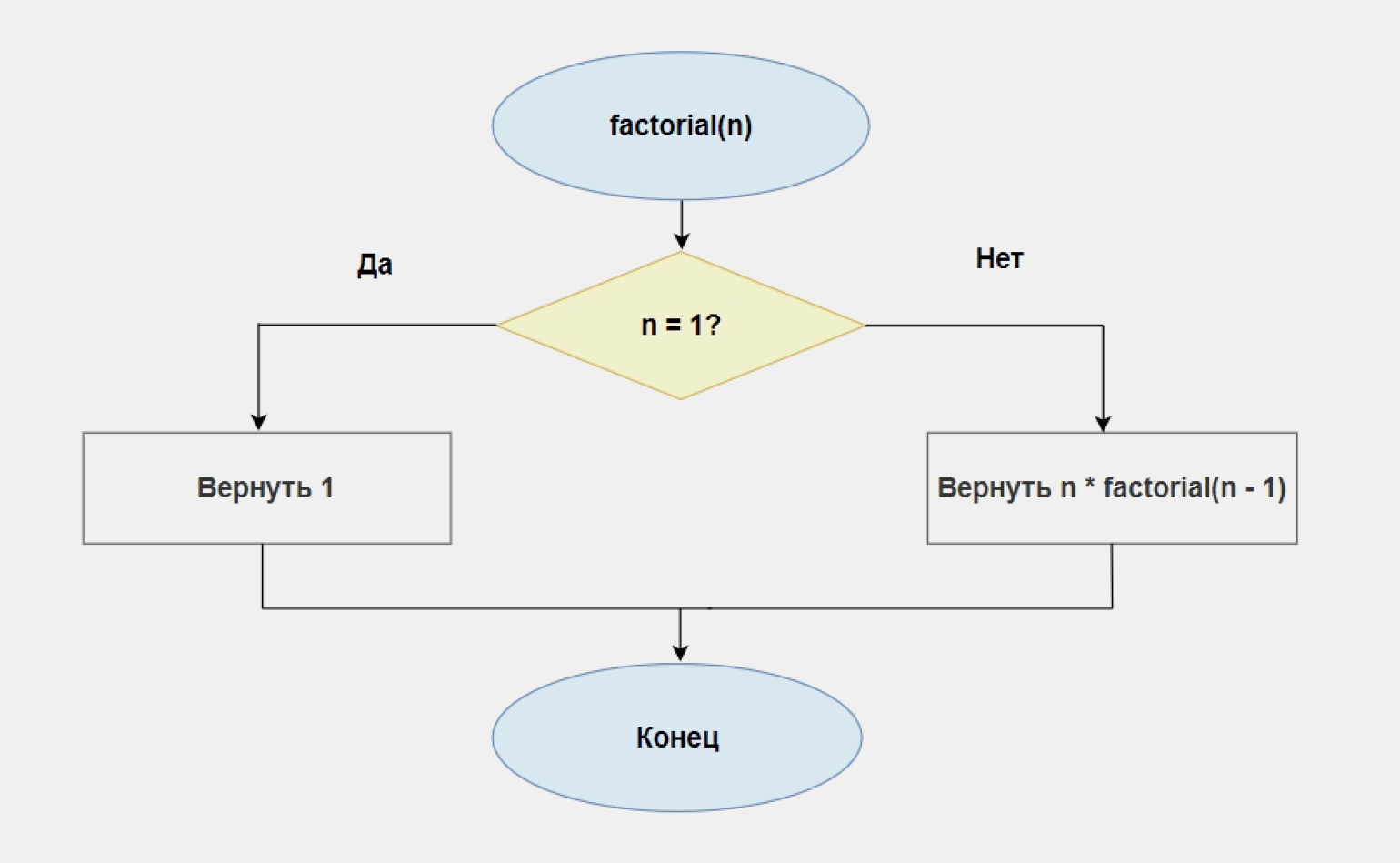
Пример. Пользователь вводит число n. Посчитайте его факториал и выведите результат на экран.
#функция, которая вызывает саму себя def factorial(n): if n == 1: return 1 #когда функция возвращает значение, #она вызывает себя, но с аргументом n - 1 return n * factorial(n - 1)
Вот как выглядит блок-схема рекурсивного алгоритма:
На практике чисто последовательные, условные или циклические алгоритмы встречаются редко, но вместе они позволяют создать решение любой сложности.
Есть и другие классификации алгоритмов. Например, по множеству решаемых задач их можно разделить на численные, поисковые, сортировочные, строковые, сетевые и криптографические. А по точности получаемых результатов — на нормальные и стохастические (вероятностные).
Если хотите изучить алгоритмы более подробно, начните с простых и увлекательных книг по computer science:
- «Грокаем алгоритмы», Адитья Бхаргава;
- «Теоретический минимум по Computer Science», Владстон Фило;
- «Гид по Computer Science», Вильям Спрингер.
Когда познакомитесь с основными алгоритмами и научитесь решать с их помощью стандартные задачи, переходите к более серьёзной литературе. Например, прочитайте Computer Science Роберта Седжвика и «Алгоритмы» Рода Стивенса.
У «Яндекса» есть бесплатные тренировки с разбором алгоритмических задач и распространённых ошибок. А попрактиковаться, закрепить теорию и подготовиться к техническому интервью можно на LeetCode — там есть сотни задач разной сложности и для разных языков программирования.

Научитесь: Профессия Python-разработчик
Узнать больше
Алгоритм — это четкая последовательность действий, выполнение которой дает какой-то заранее известный результат. Проще говоря, это набор инструкций для конкретной задачи. Известнее всего этот термин в информатике и компьютерных науках, где под ним понимают инструкции для решения задачи эффективным способом.
Сейчас под этим словом понимают любые последовательности действий, которые можно четко описать и разделить на простые шаги и которые приводят к достижению какой-то цели. Например, пойти на кухню, налить воду и положить в нее пакетик чая — это алгоритм для выполнения задачи «Заварить чай».
Алгоритмы в информатике — инструкции для компьютеров, набор шагов, который описывается программным кодом. Существуют конкретные алгоритмы для тех или иных действий, причем некоторые из них довольно сложные. Одна из целей использования алгоритмов — делать код эффективнее и оптимизировать его.
Кто пользуется алгоритмами
В общем смысле — абсолютно все живые и некоторые неживые существа, потому что любую последовательность действий, ведущую к цели, можно считать алгоритмом. Поиск еды животным — алгоритм, движения робота тоже описываются алгоритмом.
В узком смысле, в котором понятие используется в компьютерных науках, алгоритмами пользуются разработчики, некоторые инженеры и аналитики, а также специалисты по машинному обучению, тестировщики и многие другие. Это одно из ключевых понятий в IT.
Для чего нужны алгоритмы
Алгоритмы в информатике нужны для эффективного решения различных задач, в том числе тех, выполнение которых «в лоб» имеет высокую сложность или вовсе невозможно. На практике существуют алгоритмы практически для чего угодно: сортировки, прохождения по структурам данных, поиска элементов, фильтрации информации, математических операций и так далее.
Например, отсортировать массив можно в ходе полного перебора — это самое очевидное решение. А можно воспользоваться алгоритмом быстрой сортировки: он сложнее и не так очевиден, зато намного быстрее работает и не так сильно нагружает мощности компьютера. Строго говоря, полный перебор — это тоже алгоритм, но очень простой.
Существуют алгоритмически неразрешимые задачи, для решения которых нет и не может существовать алгоритма. Но большинство задач в IT разрешимы алгоритмически, и алгоритмы активно используются в работе с ними.
Алгоритмы применяются во всех направлениях IT и во многих других отраслях. Инструкции для автоматизированного станка или линии производства — алгоритмы, рецепт блюда — тоже.
Свойства алгоритмов
Дискретность. Алгоритм — не единая неделимая структура, он состоит из отдельных маленьких шагов, или действий. Эти действия идут в определенном порядке, одно начинается после завершения другого.
Результативность. Выполнение алгоритма должно привести к какому-либо результату и не оставлять неопределенности. Результат может в том числе оказаться неудачным — например, алгоритм может сообщить, что решения нет, — но он должен быть.
Детерминированность. На каждом шаге не должно возникать разночтений и разногласий, инструкции должны быть четко определены.
Массовость. Алгоритм обычно можно экстраполировать на похожие задачи с другими исходными данными — достаточно поменять изначальные условия. Например, стандартный алгоритм по решению квадратного уравнения останется неизменным вне зависимости от того, какие числа будут использоваться в этом уравнении.
Понятность. Алгоритм должен включать только действия, известные и понятные исполнителю.
Конечность. Алгоритмы конечны, они должны завершаться и выдавать результат, в некоторых определениях — за заранее известное число шагов.
Какими бывают алгоритмы
Несмотря на слово «последовательность», алгоритм не всегда описывает действия в жестко заданном порядке. Особенно это актуально сейчас, с распространением асинхронности в программировании. В алгоритмах есть место для условий, циклов и других нелинейных конструкций.
Линейные. Это самый простой тип алгоритма: действия идут друг за другом, каждое начинается после того, как закончится предыдущее. Они не переставляются местами, не повторяются, выполняются при любых условиях.
Ветвящиеся. В этом типе алгоритма появляется ветвление: какие-то действия выполняются, только если верны некоторые условия. Например, если число меньше нуля, то его нужно удалить из структуры данных. Можно добавлять и вторую ветку: что делать, если условие неверно — например, число больше нуля или равно ему. Условий может быть несколько, они могут комбинироваться друг с другом.
Циклические. Такие алгоритмы выполняются в цикле. Когда какой-то блок действий заканчивается, эти действия начинаются снова и повторяются некоторое количество раз. Цикл может включать в себя одно действие или последовательность, а количество повторений может быть фиксированным или зависеть от условия: например, повторять этот блок кода, пока в структуре данных не останется пустых ячеек. В некоторых случаях цикл может быть бесконечным.
Рекурсивные. Рекурсия — это явление, когда какой-то алгоритм вызывает сам себя, но с другими входными данными. Это не цикл: данные другие, но «экземпляров» работающих программ несколько, а не одна. Известный пример рекурсивного алгоритма — расчет чисел Фибоначчи.
Рекурсия позволяет изящно решать некоторые задачи, но с ней надо быть осторожнее: такие алгоритмы могут сильно нагружать ресурсы системы и работать медленнее других.
Вероятностные. Такие алгоритмы упоминаются реже, но это довольно интересный тип: работа алгоритма зависит не только от входных данных, но и от случайных величин. К ним, например, относятся известные алгоритмы Лас-Вегас и Монте-Карло.
Основные и вспомогательные. Это еще один вид классификации. Основной алгоритм решает непосредственную задачу, вспомогательный решает подзадачу и может использоваться внутри основного — для этого там просто указываются его название и входные данные. Пример вспомогательного алгоритма — любая программная функция.
Графическое изображение алгоритмов
Алгоритмы могут записывать текстом, кодом, псевдокодом или графически — в виде блок-схем. Это специальные схемы, состоящие из геометрических фигур, которые описывают те или иные действия. Например, начальная и конечная точка на схеме — соответственно, начало и конец алгоритма, параллелограмм — ввод или вывод данных, ромб — условие. Простые действия обозначаются прямоугольниками, а соединяются фигуры с помощью стрелок — они показывают последовательности и циклы.
В схемах подписаны конкретные действия, условия, количество повторений циклов и другие детали. Это позволяет нагляднее воспринимать алгоритмы.
Сложность алгоритма
Понятие «сложность» — одно из ключевых в изучении алгоритмов. Оно означает не то, насколько трудно понять тот или иной метод, а ресурсы, затраченные на вычисление. Если сложность высокая, алгоритм будет выполняться медленнее и, возможно, тратить больше аппаратных ресурсов; такого желательно избегать.
Сложность обычно описывают большой буквой O. После нее в скобках указывается значение, от которого зависит время выполнения. Это обозначение из математики, которое описывает поведение разных функций.
Какой бывает сложность. Полностью разбирать математическую O-нотацию, как ее называют, мы не будем — просто перечислим основные обозначения сложности в теории алгоритмов.
- O(1) означает, что алгоритм выполняется за фиксированное константное время. Это самые эффективные алгоритмы.
- O(n) — это сложность линейных алгоритмов. n здесь и дальше обозначает размер входных данных: чем больше n, тем дольше выполняется алгоритм.
- O(n²) тоже означает, что чем больше n, тем выше сложность. Но зависимость тут не линейная, а квадратичная, то есть скорость возрастает намного быстрее. Это неэффективные алгоритмы, например с вложенными циклами.
- O(log n) — более эффективный алгоритм. Скорость его выполнения рассчитывается логарифмически, то есть зависит от логарифма n.
- O(√n) — алгоритм, скорость которого зависит от квадратного корня из n. Он менее эффективен, чем логарифмический, но эффективнее линейного.
Существуют также O(n³), O(nn) и другие малоэффективные алгоритмы с высокими степенями. Их сложность растет очень быстро, и их лучше не использовать.
Графическое описание сложности. Лучше разобраться в сложности в O-нотации поможет график. Он показывает, как изменяется время выполнения алгоритма в зависимости от размера входных данных. Чем более пологую линию дает график, тем эффективнее алгоритм.
O-нотацию используют, чтобы оценить, эффективно ли использовать ту или иную последовательность действий. Если данные большие или их много, стараются искать более эффективные алгоритмы, чтобы ускорить работу программы.
Использование алгоритмов в IT
Мы приведем несколько примеров использования разных алгоритмов в отраслях программирования. На самом деле их намного больше — мы взяли только часть, чтобы помочь вам понять практическую значимость алгоритмов.
Разработка ПО и сайтов. Алгоритмы используются для парсинга, то есть «разбора» структур с данными, таких как JSON. Парсинг — одна из базовых задач, например в вебе. Также алгоритмы нужны при отрисовке динамических структур, выводе оповещений, настройке поведения приложения и многом другом.
Работа с данными. Очень активно алгоритмы применяются при работе с базами данных, файлами, где хранится информация, структурами вроде массивов или списков. Данных может быть очень много, и выбор правильного алгоритма позволяет ускорить работу с ними. Алгоритмы решают задачи сортировки, изменения и удаления нужных элементов, добавления новых данных. С их помощью наполняют и проходят по таким структурам, как деревья и графы.
Отдельное значение алгоритмы имеют в Big Data и анализе данных: там они позволяют обработать огромное количество информации, в том числе сырой, и не потратить на это слишком много ресурсов.
Поисковые задачи. Алгоритмы поиска — отдельная сложная отрасль. Их выделяют в отдельную группу, в которой сейчас десятки разных алгоритмов. Поиск важен в науке о данных, в методах искусственного интеллекта, в аналитике и многом другом. Самый очевидный пример — поисковые системы вроде Google или Яндекса. Кстати, подробности об используемых алгоритмах поисковики обычно держат в секрете.
Машинное обучение. В машинном обучении и искусственном интеллекте подход к алгоритмам немного другой. Если обычная программа действует по заданному порядку действий, то «умная машина» — нейросеть или обученная модель — формирует алгоритм для себя сама в ходе обучения. Разработчик же описывает модель и обучает ее: задает ей начальные данные и показывает примеры того, как должен выглядеть конечный результат. В ходе обучения модель сама продумывает для себя алгоритм достижения этого результата.
Такие ИИ-алгоритмы могут быть еще мощнее обычных и используются для решения задач, которые разработчик не в силах разбить на простые действия сознательно. Например, для распознавания предметов нужно задействовать огромное количество процессов в нервной системе: человек просто физически не способен описать их все, чтобы повторить программно.
В ходе создания и обучения модели разработчик тоже может задействовать алгоритмы. Например, алгоритм распространения ошибки позволяет обучать нейросети.
Алгоритм. Свойства алгоритмов.
Блок-схемы. Алгоритмические языки
Код ОГЭ: 1.3.1. Алгоритм, свойства алгоритмов, способы записи алгоритмов.
Блок-схемы. Представление о программировании
Понятие алгоритма является одним из основных понятий вычислительной математики и информатики.
■ Алгоритм
— строго определенная последовательность действий для некоторого исполнителя, приводящая к поставленной цели или заданному результату за конечное число шагов.
Любой алгоритм составляется в расчете на конкретного исполнителя с учетом его возможностей. Исполнитель — субъект, способный исполнять некоторый набор команд. Совокупность команд, которые исполнитель может понять и выполнить, называется системой команд исполнителя.
Для выполнения алгоритма исполнителю недостаточно только самого алгоритма. Выполнить алгоритм — значит применить его к решению конкретной задачи, т. е. выполнить запланированные действия по отношению к определенным входным данным. Поэтому исполнителю необходимо иметь исходные (входные) данные — те, что задаются до начала алгоритма.
В результате выполнения алгоритма исполнитель должен получить искомый результат — выходные данные, которые исполнитель выдает как результат выполненной работы. В процессе работы исполнитель может создавать и использовать данные, не являющиеся выходными, — промежуточные данные.
Свойства алгоритмов
Алгоритм должен обладать определенными свойствами. Наиболее важные свойства алгоритмов:
- Дискретность. Процесс решения задачи должен быть разбит на последовательность отдельных шагов — простых действий, которые выполняются одно за другим в определенном порядке. Каждый шаг называется командой (инструкцией). Только после завершения одной команды можно перейти к выполнению следующей.
- Конечность. Исполнение алгоритма должно завершиться за конечное число шагов; при этом должен быть получен результат.
- Понятность. Каждая команда алгоритма должна быть понятна исполнителю. Алгоритм должен содержать только те команды, которые входят в систему команд его исполнителя.
- Определенность (детерминированность). Каждая команда алгоритма должна быть точно и однозначно определена. Также однозначно должно быть определено, какая команда будет выполняться на следующем шаге. Результат выполнения команды не должен зависеть ни от какой дополнительной информации. У исполнителя не должно быть возможности принять самостоятельное решение (т. е. он исполняет алгоритм формально, не вникая в его смысл). Благодаря этому любой исполнитель, имеющий необходимую систему команд, получит один и тот же результат на основании одних и тех же исходных данных, выполняя одну и ту же цепочку команд.
- Массовость. Алгоритм предназначен для решения не одной конкретной задачи, а целого класса задач, который определяется диапазоном возможных входных данных.
Способы представления алгоритмов:
- словесная запись (на естественном языке). Алгоритм записывается в виде последовательности пронумерованных команд, каждая из которых представляет собой произвольное изложение действия;
- блок–схема (графическое изображение). Алгоритм представляется с помощью специальных значков (геометрических фигур) — блоков;
- формальные алгоритмические языки. Для записи алгоритма используется специальная система обозначений (искусственный язык, называемый алгоритмическим);
- псевдокод. Запись алгоритма на основе синтеза алгоритмического и обычного языков. Базовые структуры алгоритма записываются строго с помощью элементов некоторого базового алгоритмического языка.
Словесная запись алгоритма
Произвольное изложение этапов алгоритма на естественном языке имеет свои недостатки. Словесные описания строго не формализуемы, поэтому может быть нарушено свойство определенности алгоритма: исполнитель может неточно понять описание этапа алгоритма. Словесная запись достаточно многословна. Сложные задачи трудно представить в словесной форме.
■ Пример 1. Записать в словесной форме правило деления обыкновенных дробей.
Решение.
Шаг 1. Числитель первой дроби умножить на знаменатель второй дроби.
Шаг 2. Знаменатель первой дроби умножить на числитель второй дроби.
Шаг 3. Записать дробь, числителем которой являет результат выполнения шага 1, знаменателем — результат выполнения шага 2.
Описанный алгоритм применим к любым двум обыкновенным дробям. В результате его выполнения будут получены выходные данные — результат деления двух дробей (исходных данных).
Формальные исполнители алгоритма
Формальный исполнитель — это исполнитель, который выполняет все команды алгоритма строго в предписанной последовательности, не вникая в его смысл, не внося ничего в алгоритм и ничего не отбрасывая. Обычно под формальным исполнителем понимают технические устройства, автоматы, роботов и т. п. Компьютер можно считать формальным исполнителем.
Программы на языке произвольного формального исполнителя могут состоять только из элементарных команд, которые входят в его систему (которые исполнитель «понимает»).
Исполнитель может иметь свою среду (например, систему координат, клеточное поле и др.). Среда исполнителя — это совокупность объектов, над которыми он может выполнять определенные действия (команды), и связей между этими объектами. Алгоритмы в этой среде выполняются исполнителем по шагам.
■ Пример 2. Исполнитель Крот имеет следующую систему команд:
- вперед k — продвижение на указанное число шагов вперед;
- поворот s — поворот на s градусов по часовой стрелке;
- повторить m [команда1 … командаN] — повторить m раз серию указанных команд.
Какой след оставит за собой исполнитель после выполнения следующей последовательности команд?
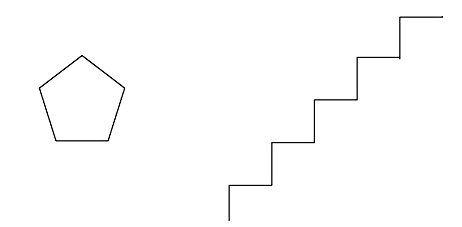
Повторить 5 [вперед 10 поворот 72]
Решение. Команда вынуждает исполнителя 5 раз повторить набор действий: пройти 10 шагов вперед и повернуть на 72° по часовой стрелке. Так как поворот происходит на один и тот же угол, то за весь путь исполнитель повернет на 5 х 72° = 360°. Поскольку все отрезки пути одинаковой длины и сумма внешних углов любого многоугольника составляет 360°, то в результате будет оставлен след в форме правильного пятиугольника со стороной в 10 шагов исполнителя.
Заметим, что если увеличить количество повторов серии команд, то исполнитель будет повторно передвигаться по тем же отрезкам (произойдет повторное движение по тому же пятиугольнику).
■ Пример 3. В системе команд предыдущего исполнителя Крот сформировать алгоритм вычерчивания пятиступенчатой лестницы (длина ступеньки — 10 шагов исполнителя).
Решение. За каждый шаг цикла должно происходить 4 действия: движение вперед на 10 шагов исполнителя, поворот на 90° по часовой стрелке, еще 10 шагов вперед и поворот на 90° против часовой стрелки (= 270° по часовой). В результате за один шаг цикла формируется ломаная из двух отрезков длиной 10 под прямым углом. За пять таких шагов сформируется 5–ступенчатая лестница (ломаная будет содержать 10 звеньев).
Повторить 5 [вперед 10 поворот 90 вперед 10 поворот 270]
Блок–схема
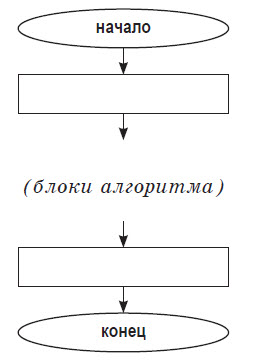
Блок–схема — наглядный способ представления алгоритма. Блок–схема отображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Определенному типу действия соответствует определенная геометрическая фигура блока. Линии, соединяющие блоки, определяют очередность выполнения действий. По умолчанию блоки соединяются сверху вниз и слева направо. Если последовательность выполнения блоков должна быть иной, используются направленные линии (стрелки).
Основные элементы блок–схемы алгоритма:
Общий вид блок–схемы алгоритма:
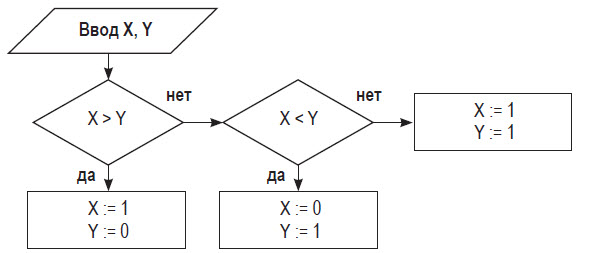
■ Пример 4. Алгоритм целочисленных преобразований представлен в виде фрагмента блок–схемы. Знаком := в нем обозначен оператор присваивания некоторого значения указанной переменной. Запись X := 1 означает, что переменная Х принимает значение 1.
Определить результат работы алгоритма для исходных данных Х = 7, Y = 12.
Решение.
- Блок ввода данных определит исходные значения переменных Х и Y (7 и 12 соответственно).
- В первом условном блоке осуществляется сравнение значений Х и Y. Поскольку условие, записанное в блоке, неверно (7 < 12), происходит переход по линии «нет».
- Во втором условном блоке выполняется второе сравнение, которое для исходных данных оказывается верным. Происходит переход по линии «да».
- Вычисляется результат выполнения алгоритма: X := 0, Y := 1.
Ответ: X := 0, Y := 1.
Алгоритмические языки
Алгоритмический язык — это искусственный язык (система обозначений), предназначенный для записи алгоритмов. Он позволяет представить алгоритм в виде текста, составленного по определенным правилам с использованием специальных служебных слов. Количество таких слов ограничено. Каждое служебное слово имеет точно определенный смысл, назначение и способ применения. При записи алгоритма служебные слова выделяют полужирным шрифтом или подчеркиванием.
В алгоритмическом языке используются формальные конструкции, но нет строгих синтаксических правил для записи команд. Различные алгоритмические языки различаются набором служебных слов и формой записи основных конструкций.
Алгоритмический язык, конструкции которого однозначно преобразуются в команды для компьютера, называется языком программирования. Текст алгоритма, записанный на языке программирования, называется программой.
Псевдокод
Псевдокод занимает промежуточное положение между естественным языком и языками программирования. Пример псевдокода — учебный алгоритмический язык. Алфавит учебного алгоритмического языка является открытым. Существенным достоинством этого языка является то, что его служебные слова, конструкции и правила записи алгоритма весьма схожи с теми, что применяются в распространенных языках программирования. Благодаря этому учебный алгоритмический язык позволяет легче освоить основы программирования.
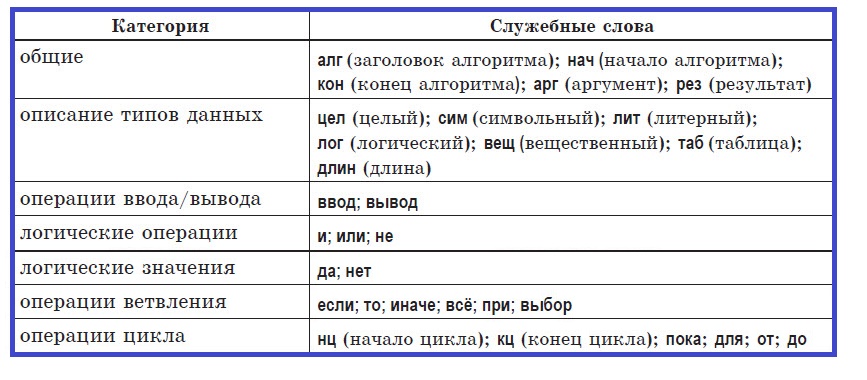
Служебные слова учебного алгоритмического языка:
Стандартная структура алгоритма
Представление алгоритма на алгоритмическом языке (в том числе и языке программирования) состоит из двух частей. Первая часть — заголовок — задает название алгоритма и включает описание переменных, которые используются в нем. Вторая часть — тело алгоритма — содержит последовательность команд алгоритма.
Общий вид записи алгоритма на учебном алгоритмическом языке:
В начале заголовка записывается служебное слово алг, после чего указывается имя алгоритма. Описание переменных, являющихся аргументами алгоритма и его результатами, приводится после названия в круглых скобках.
В следующих строках конкретизируют, какие именно переменные являются аргументами алгоритма (входными данными), а какие — его результатами (выходными данными). Для этого после служебного слова арг приводится список имен переменных–аргументов; в следующей строке после служебного слова рез приводится список имен переменных–результатов.
Между служебными словами нач и кон размещается тело алгоритма — конечная последовательность команд, выполнение которых предписывает алгоритм. Команды алгоритма записывают одну за одной в отдельных строках. В случае необходимости можно записать две или более команд в одной строке, тогда соседние команды разделяют точкой с запятой. Если в алгоритме применяются промежуточные переменные, их описание приводят в начальной строке тела алгоритма рядом со словом нач.
Примеры заголовков алгоритмов:
В первом примере алгоритм имеет название Объем_шара, один вещественный аргумент Радиус и один вещественный результат Объем. Во втором примере алгоритм под названием Choice имеет три аргумента — целые M и N и логический b, а также два результата — вещественные Var1 и Var2.
Пример алгоритма вычисления гипотенузы прямоугольного треугольника:
На вход алгоритму даются два вещественных аргумента a и b (величины катетов), результатом является вещественная переменная с (гипотенуза). Для ее расчета используется функция вычисления квадратного корня sqrt.
Описание величин и действия над ними
При описании алгоритма необходимо указать названия (обозначения) всех величин, которые будут в нем найдены или использованы.
При представлении алгоритма решения в виде блок–схемы выбранные обозначения величин приводятся отдельно от блок–схемы (как объяснение к ней). Если алгоритм представлен на языке программирования, то характеристика обрабатываемых величин включается в программу. Учебный алгоритмический язык также предусматривает описание величин, используемых в алгоритме.
Все величины в алгоритме разделяют на постоянные (константы) и переменные. Константа не может изменять свои значения в процессе работы алгоритма. Переменная может приобретать различные значения, которые сохраняются до тех пор, пока она не получит новое значение. Переменным величинам назначают имена. Таким образом, переменная — это именуемая величина, которая в процессе выполнения алгоритма может приобретать и хранить различные значения.
В алгоритмическом языке не существует специальных правил именования переменных. Однако их названия не должны совпадать со служебными словами алгоритмического языка. Во многих языках программирования для имен можно использовать только латинские буквы, цифры, знак подчеркивания. Имена обязательно должны начинаться с буквы, при этом строчные и прописные буквы в именах не различаются. В одном алгоритме не могут существовать разные объекты с одинаковыми именами. Все имена являются уникальными. Имена переменных и констант стараются выбирать так, чтобы они напоминали их смысл. Например, имена переменных и констант: S, p12, result, итог.
При представлении алгоритма на алгоритмическом языке именуются не только величины, но и сам алгоритм, и другие объекты. Имя алгоритма выбирают так же, как и имена переменных.
Величина — переменная, с которой связывается определенное множество значений. Этой величине присваивается имя (в языках программирования его называют идентификатор).
Значение — то, чему равна переменная в конкретный момент. Значение переменной можно задать двумя способами: присваиванием и с помощью процедуры ввода.
Тип переменной определяет диапазон всех значений, которые может принимать данная переменная, и допустимые для нее операции. Существует несколько предопределенных типов переменных. К стандартным типам относятся числовые, литерные и логические типы.
Числовой тип предназначен для обработки числовых данных. Различают целый и вещественный числовые типы. Целый тип в учебном алгоритмическом языке обозначается служебным словом цел, к нему относятся целые числа некоторого определенного диапазона. Они не могут иметь дробной части, даже нулевой. Число 123,0 является не целым, а вещественным числом. Вещественные величины относятся к вещественному типу данных и обозначаются в учебном алгоритмическом языке служебным словом вещ. Такие величины могут отображаться двумя способами: в форме с фиксированной запятой (например, 0,0511 или –712,3456) и с плавающей запятой (те же примеры: 5,11*10-2 и –7,123456*102).
Над числовыми данными можно выполнять арифметические операции и операции сравнения.
Над целыми числами можно также выполнять две операции целочисленного деления div и mod. Операция div обозначает деление с точностью до целых чисел (остаток от деления игнорируется). Операция mod позволяет узнать остаток при делении с точностью до целых чисел. Например, результатом операции 100 div 9 будет число 11, а результатом 100 mod 9 — число 1.
Литерный тип представляет собой символы и строки, он дает возможность работать с текстом. Литерные величины — это произвольные последовательности символов. Эти последовательности заключаются в двойные кавычки: «результат», «sum_price». В качестве символов могут быть использованы буквы, цифры, знаки препинания, пробел и некоторые другие специальные знаки (возможными символами могут быть символы таблицы ASCII). В учебном алгоритмическом языке литерные величины обозначаются лит.
Над литерными величинами возможны операции сравнения и слияния. Сравнение литерных величин производится в соответствии с их упорядочением: «a» < «b», «b» < «с» и т. д. Слияние (конкатенация) литерных величин приводит к образованию новой величины: «пол» + «е» образует «поле».
Логический тип определяет логические переменные, которые могут принимать только два значения — истина (True) или ложь (False). Над логическими величинами можно выполнять все стандартные логические операции.
Команды учебного алгоритмического языка
Учебный алгоритмический язык использует следующие команды для реализации алгоритма:
ОПЕРАЦИЯ ПРИСВАИВАНИЯ
Ко всем типам величин может быть применена операция присваивания, которая обозначается знаком «:=» и служит для вычисления выражения, стоящего справа, и присваивания его значения переменной, указанной слева. Например, если переменная H имела значение 12, а переменная М — значение 3, то после выполнения оператора присваивания H := М + 10 значение переменной H изменится и станет равным 13.
Вычисления в операторе присваивания выполняются справа налево: сначала необходимо вычислить значение выражения справа от знака присваивания. Поэтому допустимы конструкции вида H := Н + 10. В этом случае сначала будет вычислено выражение в правой части (12 + 10), а его результат будет присвоен в качестве нового значения переменной Н (значение 22).
Для оператора присваивания обязательно должны быть определены значения всех переменных в его правой части. Кроме того, типы данных в левой и правой части должны соответствовать друг другу.
ВВОД И ВЫВОД ДАННЫХ
В процессе работы алгоритма происходит обработка исходных данных для получения выходных (результирующих) данных. В процессе этого преобразования могут быть найдены некоторые промежуточные результаты. Входные данные должны быть переданы алгоритму («введены»), а по окончании работы алгоритм должен вывести результат.
При записи алгоритма с помощью блок–схемы ввод и вывод данных отображаются с помощью блоков ввода/вывода (параллелограммов). При этом только указывается перечень данных для ввода или вывода, а сам процесс не детализируется.
Описание алгоритма средствами псевдокода может вовсе не предусматривать команды ввода или вывода данных. В заголовке алгоритма указывается, какие данные являются аргументами, какие — результатами работы алгоритма. Считается, что аргументы будут предоставлены до выполнения алгоритма, результаты будут выведены после его выполнения, и описывается лишь процесс превращения аргументов в результаты.
В записи алгоритма с помощью учебного алгоритмического языка для операций ввода/вывода используются команды ввод и вывод. После этих служебных слов указывается список ввода или вывода. Элементы этих списков перечисляются через запятую.
Список ввода может содержать только имена переменных. После выполнения команды ввод алгоритм получит значения перечисленных в списке переменных.
Список вывода может содержать имена переменных, константы и выражения. Если в списке вывода указано имя переменной, будет выведено ее значение. Если список вывода содержит выражение, будет выведен результат его вычисления. Текстовые константы следует записывать в списке вывода в кавычках (выводиться они будут без кавычек).
Если при выполнении алгоритма ввести значения 20 и 10, то переменная v примет значение 20, а переменная t — значение 10. По окончании работы алгоритма будет выведен результат:
Путь 200 м
Тот же результат был бы получен, если бы изменить строку вывода на
вывод «Путь «, v * t, » м»
Конспект по информатике «Алгоритм. Свойства алгоритмов. Блок-схемы. Алгоритмические языки».
Вернуться к Списку конспектов по информатике.