Руководство по геогебре

GeoGebra (Геогебра) — это динамическая математическая программа, которая объединяет геометрию, алгебру и исчисления. Она разработана для изучения и преподавания математики в школах Маркусом Гогенвартером (Markus Hohenwarter) и международым сообществом программистов. Это руководство относится к текущей версии (4.0). Геогебра обратно совместима со всеми предыдущими версиями с небольшими отличиями.

Установка GeoGebra

Руководство по установке поможет вам установить GeoGebra в различных операционных системах.

Создание динамических чертежей

Чертежи в GeoGebra состоят из математических объектов нескольких типов, которые могут быть созданы с помощью инструментов or команд. В первых построениях вам могут помочь учебники.

Интерфейс GeoGebra

Главное окно разделено на Виды. По умолчанию слева расположена Панель объектов, а справа — Полотно. Над ними могут быть размещены Панель меню и Панель инструментов, а под ними — Шаги построения. Многие функции GeoGebra могут быть доступны с помощь горячих клавиш. GeoGebra также включает специальные возможности, такие как Клавиатура.

Публикацию

Закончив чертёж, вы можете:

• сохранить его в файл (формат файла GeoGebra),
• создать Интерактивный чертеж с помощью аплета Java или HTML5,
• распечатать чертёж, в том числе и с протоколом,
• Экспортировать в изображение в форматах PNG, SVG, PDF, EPS, EMF или LaTeX и Asymptote,
• загрузить на GeoGebra.en:Manual:Main Page

Использование
ПО Geogebra на уроках математики

Адрес сайта: https://www.geogebra.org/

ГЛАВА
I. ПОДГОТОВКА К РАБОТЕ С ПО GEOGEBRA

§1. Установка
ПО GEOGEBRA на компьютер GeoGebra — это бесплатная, кроссплатформенная
динамическая математическая программа для всех уровней образования, включающая
в себя геометрию, алгебру, таблицы, графы, статистику и арифметику, в одном
удобном для использования пакете.

Для того, чтобы начать работать,
сначала нужно установить программу Geogebra на компьютер. В браузере строке
ввода адреса вводим ссылку на официальный сайт https://www.geogebra.org/
и переходим в раздел AppDownloads.

Откроется страница с различными
приложениями. Выбираем Graphing Calculator и нажимаем DOWNLOAD.

После того, как файл будет скачан,
нужно будет дважды кликнуть по нему мышкой. Появится диалоговое окно, в котором
мы нажимаем кнопку «Запустить». Через некоторое время откроется сама программа.

§2.
Знакомство с интерфейсом ПО GEOGEBRA

Итак, мы готовы приступить к работе.
Для начала давайте разберемся с тем, что мы видим перед собой.

Для
того, чтобы перейти в раздел «Геометрия» над полем ввода выбрать значок

После этого слева откроется Панель инструментов
«Геометрия»:

 

Приступим к изучению инструментов,
которые мы сможем использовать на уроках геометрии. Для того, чтобы увидеть
весь набор инструментов, нужно будет нажать на кнопку «More» в нижнем левом
углу Панели инструментов.

Первый
блок инструментов Basic Tools.

Самый важный из инструментов
первого блока – инструмент «Перемещать». При помощи него можно выделять,
перемещать и изменять положение объектов в координатной плоскости. Для того,
чтобы выделить несколько объектов, нужно зажать клавишу CRTL и последовательно
выделить необходимые объекты.

Инструмент «Точка» позволяет в координатной
плоскости построить точку. Точка будет обозначаться заглавной латинской буквой.

Инструмент «Ползунок»
задает параметр, и границы его изменения. Этот  инструмент позволяет создавать
анимированные объекты и показывает, как будет изменяться положение объектов в
системе координат в зависимости, от заданного параметра.

Инструмент «Пересечение»
позволяет построить точку пересечения двух объектов. Для того, чтобы построить
точку пересечения двух объектов,  необходимо выбрать инструмент «Пересечение»,
а затем последовательно

выбрать два объекта, точку пересечения которых нужно
построить.

Блок
Lines 

 

Основными инструментами, которыми мы
будем пользоваться в блоке Lines , являются «Отрезок», «Прямая, «Луч» и
«Вектор».

Инструмент «Отрезок» позволяет построить отрезок по
двум точкам. Для того, чтобы построить отрезок, необходимо

—    выбрать
инструмент «Отрезок»

—    отметить
две точки в координатной плоскости.

Инструмент «Прямая» позволяет в координатной
плоскости построить прямую. Для того, чтобы построить прямую, необходимо

—    выбрать
инструмент «Прямая»

—    отметить
две точки в координатной плоскости.

Инструмент «Луч» позволяет в координатной плоскости
построить луч. Для того, чтобы построить луч, необходимо        — выбрать
инструмент «Луч»

—    отметить
первую точку

—    отметить
вторую точку, выбрав направление луча

Инструмент «Вектор»
позволяет в координатной плоскости построить вектор. Для того, чтобы построить
вектор, необходимо

—    выбрать
инструмент «Вектор»

—    отметить
первую точку

—    отметить
вторую точку, выбрав направление вектора

Блок
Polygons

 

Этот блок содержит инструменты, которые позволяют
строить многоугольники.

Инструмент «Многоугольник» позволяет построить
произвольный многоугольник. Для того, чтобы построить многоугольник необходимо

—    выбрать
инструмент «Многоугольник»

—    отметить
первую точку

—    последовательно
отметить нужное количество точек

—    вернуться
к первой точке и мышкой указать на нее. Таким образом, завершить построение

Инструмент «Правильный многоугольник» позволяет
построить правильный многоугольник. Для того, чтобы построить правильный
многоугольник необходимо

—

—    выбрать
инструмент «Правильный отметить первую точку   многоугольник»

—    отметить
вторую точку

—    в
открывшемся окне ввести нужное количество вершин правильного многоугольника

Блок
Circles

 

Данный блок позволяет различными способами
построить окружности.

«Окружность по центру и точке». Чтобы построить окружность
необходимо:

—    выбрать
инструмент «Окружность по центру и точке»

—    отметить
центр окружности

—    отметить
произвольным точку, лежащую на окружности.

«Окружность по центру и радиусу». Чтобы построить
окружность по центру и радиусу необходимо:

—    выбрать
инструмент «Окружность по центру и радиусу»

—    отметить
центр окружности

—    ввести в
открывшемся окне значение радиуса

«Окружность по трем точкам». Чтобы построить окружность по
трем точкам, необходимо:

—    выбрать
инструмент «Окружность»

—   
отметить последовательно три точки, через которые будет проходить
окружность.

ГЛАВА
II. ПРОСТЕЙШИЕ ПОСТРОЕНИЯ В GEOGEBRA

§1. Построение плоских фигур Задача 1. 

а) Построить в плоскости три точки 𝐴, 𝐵 и 𝐶. 

б) Поменять их цвета на красный, черный и зеленый
соответственно.

1.                     
Выбрать инструмент «Точка»

2.                     
В координатной плоскости произвольным образом отметить точки 𝐴, 𝐵 и 𝐶.

3.

4.

палитра цветов, в которой мы выбираем красный цвет.

 

7.
Выполните эти же действия для того, чтобы раскрасить оставшиеся точки в
черный и зеленый цвета.

 

Задача
2. 

а) Построить произвольный восьмиугольник. 

б) Стороны восьмиугольника раскрасить в четыре
разных цвета.

в) Две стороны восьмиугольника сделать
пунктирными.  

Прежде, чем мы приступим к решению
следующей задачи, нам необходимо расчистить место для построения. Для того,
чтобы очистить координатную плоскость, можно последовательно выделять мышкой
элементы и нажимать клавишу DELETE на клавиатуре. Но, конечно, все построения
можно оставить и выполнять построения рядом. 

Итак, решение.

1.                      
Выбрать элемент «Многоугольник» на Панели инструментов и
выполнить построение восьмиугольника по точкам.

 

У меня получился вот такой многоугольник. 

2.                      
Рассмотрите многоугольник, который получился у вас. Обратите
внимание на следующие детали:

•
Каждый отрезок, который является стороной многоугольника имеет два
названия: первое – двумя заглавными латинскими буквами, а второе – маленькой
латинской буквой. Например, на моем рисунке отрезок 𝐴𝐵 также назван просто буквой 𝑎. Иногда двойное имя
каждого элемента на чертеже сильно загромождает рисунок. Однако, Geogebra дает возможность
одно из названий убрать. Уберем название каждого отрезка. Для этого 

—  выберем инструмент
«Перемещать» и мышкой выделим отрезок 𝑎.
Он должен стать подсвеченным. 

—  появится меню для
работы с отрезком. В нем необходимо выбрать три вертикально расположенных точки

—  в выпавшем меню
выбрать пункт «Настройки»

—  справа появится меню
для работы с объектом. В этом меню нужно убрать галочку рядом со словами
«Показывать обозначение»

Если вы все сделали верно, то
название отрезка 𝑎
исчезнет. Выполните эти действия для оставшихся отрезков. В результате
получается менее нагроможденный чертеж

 

•     Продолжим
изучать многоугольник. Обратите внимание на расположение

точек 𝐴, 𝐵, 𝐶, 𝐷,
𝐸, 𝐹 и 𝐺. Точки 𝐵
и 𝐶 хорошо видны на рисунке. А вот расположение остальных точек
не очень удобно для восприятия. Попробуем это исправить. 

Для того, чтобы переместить имя точки необходимо навести
курсор мыши на имя точки так, чтобы курсор принял вид «Пальца». После этого, не
отпуская левую кнопку мыши переместить имя точки туда, где вы хотите, чтобы оно
было. У меня в результате всех перемещений получился такой рисунок:

•    
И еще один момент, на который я бы хотела

обратить ваше внимание. Если вы выполняете построение
многоугольника при помощи инструмента «Многоугольник», то внутренняя область
многоугольника по умолчанию будет окрашиваться в голубой цвет. Работать можно и
с таким рисунком. Но будет полезно узнать и то, как внутреннюю область сделать
прозрачной.

Для того, чтобы сделать внутреннюю область прозрачной,
необходимо, курсор мыши поместить во внутреннюю часть многоугольника так, чтобы
он принял форму «Пальца». После этого нужно один раз нажать левой кнопкой мыши
на внутренней области многоугольника. Появится меню для работы с
многоугольником. 

В этом меню выбираем «Ведро с
краской». У вас появится палитра цветов. Обратите внимание на то, что когда мы
меняли цвет точки, то заливка в палитре была сплошной. Здесь же палитра
полупрозрачная. Чтобы внутренняя часть многоугольника стала прозрачной,
необходимо бегунок переместить в крайнее левой положение, чтобы вместо числа 10
появился 0.

Должно получиться так

 

3.                      
Продолжим решать задачу. Теперь нам необходимо раскрасить стороны
в четыре различных цвета. Чтобы раскрасить стороны в различные цвета,
необходимо выполнить те же действия, что и в задаче 1 б), когда мы раскрашивали
точки в различные цвета. Только теперь нам необходимо будет выделять отрезки, а
не точки. Попробуйте выполнить эти действия самостоятельно.

У меня получился такой многоугольник

 

4.                      
Далее выполним задание под буквой в). Нужно две стороны
многоугольника сделать пунктирными. Для этого одним нажатием левой кнопки мыши
выделим одну из сторон так, чтобы появилось вспомогательное меню для работы с
отрезком. В нем находим инструмент «Стиль линии». 

Нажимаем 1 раз. Появится еще одно вспомогательное
меню. В нем выбираем любой тип пунктира.

 

Теперь рисунок выглядит так:

 

Выполните эту операцию еще для 1-2 сторон
многоугольника.

Задача
3. 

а) Построить правильный семиугольник. 

б) Раскрасить все стороны правильного семиугольника
в разные цвета. 

в) Сделать внутреннюю область правильного семиугольника
невидимой.

1.                      
На панели инструментов необходимо выбрать инструмент «Правильный
многоугольник»

2.                      
Отметить в координатной плоскости первую вершину семиугольника, а
затем вторую. 

3.                      
В открывшемся окне ввести количество вершин многоугольника – 7.
Получится такой рисунок:

 

4.                      
Повторяя действия, которые вы выполнили при решении предыдущей
задачи, переместите названия вершин семиугольника так, чтобы было более удобно
для восприятия. После этого скройте обозначение объекта «Многоугольник», как вы
это делали при решении предыдущей задачи (см. страницу 8). У меня получилось
так:

 

5.                      
Вы также можете изменить цвет серых вершин на синие или любы
другие.

6.                      
Самостоятельно раскрасьте стороны семиугольника в разные цвета и
сделайте внутреннюю область семиугольника невидимой.

 

Задача
4.

а) Построить окружность по центру и точке.

б) Построить окружность по центру и радиусу.
Изменить цвет окружности.

в) Построить окружность по трем точкам. 

Используя алгоритмы на странице 5,
решите задачу 4 самостоятельно. Задача 5.

К окружности, вписанной в квадрат 𝐴𝐵𝐶𝐷,
проведена касательная, пересекающая стороны 𝐴𝐵
и 𝐴𝐷 в
точках 𝑀 и 𝑁 соответственно.

а) Докажите, что периметр треугольника 𝐴𝑀𝑁
равен стороне квадрата.

б) Прямая 𝑀𝑁 пересекает прямую 𝐶𝐷 в точке 𝑃. В каком отношении
делит сторону 𝐵𝐶
прямая, проходящая через точку 𝑃
и центр окружности, если 𝐴𝑀
: 𝑀𝐵 = 1 : 3?

Выполним чертеж к задаче в программе Geogebra. 

1.                      
Уберем координатные оси, чтобы они не нагромождали рисунок. Для
этого в любом месте координатной плоскости кликните правой кнопкой мыши и
снимите галочку напротив пункта «Показывать оси». Координатные оси исчезнут.

2.                      
Построим квадрат при помощи инструмента «Правильный
многоугольник»

3.                      
Построим окружность по трем точкам. Выбирайте любые три середины
сторон квадрата. Получается вот такой рисунок

 

4.                      
Поработаем с этим рисунком. Скроем название «многоугольник1». Для
этого кликнем левой кнопкой мыши по любой части внутренней области квадрата, в
открывшемся меню выберем три точки и далее пункт «Настройки». В открывшемся
справа окне снимите галочку с пункта «Показывать обозначение». Здесь же можно
убрать и имя окружности 𝑐.
Для этого наведите курсор мыши на окружность так, чтобы курсор принял форму
«Пальца». Кликните по окружности. В меню справа снова снимите галочку
«Показывать обозначение»

5.                      
Сделаем прозрачной внутреннюю часть квадрата, изменим цвет всех
точек на синий. Перетащите имена некоторых точек так, чтобы было удобно их
читать.

 

6.                      
Теперь будем проводить касательную. Перед тем, как приступим к
проведению касательной, рассмотрим Панель для ввода формул. Для того, чтобы
перейти на Панель для ввода формул слева найдите кнопку «Алгебра» с
изображением

Нажмите на нее. Теперь ваш экран выглядит так

 

Обратите внимание, что слева приведен
полный список объектов, которые изображены у вас на полотне. Точки с
координатами, многоугольник и окружность с уравнением ее задающим. Это
алгебраическое описание построенных вами объектов. Кстати, если мышкой нажимать
на кружочки рядом с объектами в этом списке, то объекты будут исчезать.
Например, если мы нажмем на кружок рядом с точкой 𝐴, то на рисунке эта точка исчезнет:

 

Чтобы точку вернуть, вам
необходимо снова нажать на кружок рядом с точкой 𝐴.

Вернемся к задаче. Нам нужно провести
касательную к окружности, которая пересекает стороны 𝐴𝐵 и 𝐴𝐷. Вернемся обратно на Панель
инструментов «Геометрия». Для этого выберем значок «Треугольник и окружность»
на панели справа

 

7.
Для того, чтобы построить касательную, нам необходимо выбрать точку за
пределами окружности, из которой касательная будет проведена. Например, точка 𝐻

Выберем его. Теперь чтобы
построить

Как можно увидеть, из точки проведены

Теперь рисунок выглядит так

 

9.                      
Отметим точки 𝑀
и 𝑁, которые по условию задачи являются точками пересечение
касательной и сторон 𝐴𝐵
и 𝐴𝐷 соответственно. Чтобы построить точки пересечения,
выберем инструмент «Пересечение» на Панели инструментов

 

10.                  
Чтобы построить точку пересечения, нам необходимо последовательно
выделить мышкой два объекта, для которых мы строим точку пересечения. Например,
выделим сначала сторону 𝐴𝐵,
а потом касательную. У меня появилась точка 𝐼.
Переименуем ее.

 

11.                  
Чтобы переименовать точку, кликните по ней левой кнопкой мыши, в
выпадающем меню выберите пункт «три точки», далее пункт «Настройки» 

12.                  
Справа в открывшемся меню найдите пункт «Имя» и поставьте курсор
мыши справа от имени точки. Нажмите клавишу Back Space для того, чтобы удалить
имя точки и введите новое имя – 𝑀.
Далее кликните в любом месте полотна, где изображены окружность и квадрат. Имя
точки изменится. 

 

13.                  
Для того, чтобы построить точку 𝑁,
выполните действия из пунктов 9 – 12.

 

14.                  
Приступим к решению задачи. 

а) Пусть окружность, вписанная в
квадрат, касается его стороны 𝐴𝐵
в точке 𝐸,
стороны 𝐴𝐷
– в точке 𝐹, а
прямой 𝑀𝑁
— в точке 𝑇. 

Построим         точку 𝑇
         –          точку касания окружности и прямой 𝑀𝑁. Для
этого выполним пункты 9-12.

По свойству касательных 𝑁𝐹 = 𝑁𝑇
и 𝑀𝑇 = 𝐸𝑀 и 𝐴𝐹 = 𝐴𝐸. Тогда 

𝐴𝑀 + 𝑀𝑁
+ 𝐴𝑁 = 𝐴𝑀 + 𝑀𝑇 + 𝑁𝑇
+ 𝐴𝑁 =

(𝐴𝑀 + 𝑀𝐸)
+ (𝑁𝐹 + 𝐴𝑁) =  𝐴𝐵 +  𝐴𝐷 = 𝐴𝐵

Что и требовалось доказать.

б) Прямая 𝑀𝑁
пересекает прямую 𝐶𝐷
в точке 𝑃.
Построим эту прямую и точку

пересечения 𝑀𝑁 и 𝐶𝐷. 

Для того, чтобы построить прямую 𝐶𝐷 выберем
инструмент «Прямая» и построим прямую через точки 𝐶 и 𝐷. Далее при помощи
инструмента «Пересечение» построим точку пересечения двух прямых и переименуем
ее в точку 𝑃.
(см. рис.1)

Также необходимо построить точку 𝑂 – центр окружности и
прямую, соединяющую центр окружности и точку 𝑃.
Воспользуемся инструментом «Прямая» и построим прямую по двум точкам — 𝑂 и 𝑃. (см.
рис.2)

 

                             Рис.1                                           Рис.2
                                         Рис. 3

б) Положим 𝐴𝐵 = 12𝑎, 𝑇𝑁
= 𝑁𝐹 = 𝑥. Тогда

𝐴𝑀
= 3𝑎; 𝐴𝑁 = 𝐴𝐹 − 𝑁𝐹 = 6𝑎
− 𝑥;

𝑀𝑁
= 𝑀𝑇 + 𝑇𝑁 = 3𝑎 + 𝑥;

По теореме Пифагора: 𝐴𝑀² +
𝐴𝑁² = 𝑀𝑁², то есть 9𝑎²
+ (6𝑎 − 𝑥)² = (3𝑎 + 𝑥)²; 𝑥 = 2𝑎.

Тогда 𝐴𝑁 =
4𝑎 и 𝑀𝑁
= 5𝑎. Пусть O
– центр окружности, а прямая PO пересекает стороны AD и BC
в точках L и K соответственно. (Построим прямую 𝑃𝑂 и точки пересечения этой прямой со
сторонами 𝐴𝐷 и 𝐵𝐶 в точках 𝐿
и 𝐾
соответсвенно. Для этого воспользуемся сначала инструментом

«Прямая» и построим прямую 𝑃𝑂, а затем дважды воспользуемся
инструментом «Пересечение» — см.рис.3). Из равенства треугольников DOL и
BOK следует, что DL = BK, 

поэтому ^𝐵𝐾
=
^𝐷𝐿. Окружность вписана в угол MPC, значит, PL — биссектриса
треугольника DPN,

𝐾𝐶            𝐿𝐴
который подобен
треугольнику AMN. Используя свойство биссектрисы и подобие, находим:

𝐷𝐿           𝑃𝐷          𝐴𝑀          3

= = = , откуда 𝐷𝐿 =𝐷𝑁. 𝐿𝑁 𝑃𝑁
𝑀𝑁 5

Учитывая, что 𝐷𝑁
= 𝐷𝐴 − 𝐴𝑁 = 12𝑎 − 4𝑎 = 8𝑎,
находим, что 𝐷𝐿
= 3𝑎, 𝐿𝐴 = 9𝑎. Тогда

                                                                                          𝐵𝐾       𝐷𝐿      1

                                                                                                  =         =   

                                                                                          𝐾𝐶       𝐿𝐴      3

Ответ: б) 1 : 3.

§2. Построение объемных фигур

Для того, чтобы построить объемные
фигуры в Geogebra, нам необходимо переключиться на 3D интерфейс. Для этого
выполним следующие действия:

1)     
Над Панелью
инструментов найдем значок «Три черты». (см. рис. 1). Кликнем по нему левой
кнопкой мыши.

2)     
Откроется меню
(см. рис.2). В открывшемся меню нужно выбрать пункт Apps (см.рис.2)

3)     
И в новом
открывшемся меню выбрать 3D Calculator (см.рис.3). Начнется открытие
приложения. Разверните его на весь экран.

Тогда вы увидите следующее
изображение (см. на следующей странице):

 

Часть инструментов будет повторяться.
Рассмотрим те инструменты, которые характерны для построений в пространстве.

Блок Solids

 

                                              Рис. 4                                                                     Рис.
5

Инструмент «Призма» позволяет
построить произвольную призму. Для того, чтобы построить призму, необходимо:

1)     
Выбрать
инструмент «Призма»;

2)     
Отметить нужно
количество точек в основании пирамиды в плоскости xOy;

3)     
Постройте первую
верхнюю вершину (см. рис. 5)

Инструмент «Цилиндр» позволяет
построить цилиндр по двум точкам и радиусу. Для того, чтобы построить цилиндр,
необходимо:

1)     
Выбрать
инструмент «Цилиндр»;

2)     
Отметить две
точки на оси Oz;

3)     
В открывшемся
окне ввести радиус цилиндра (см. рис. 6)

Инструмент «Конус» позволяет
построить конус по двум точкам и радиусу. Для того, чтобы построить конус,
необходимо:

1)     
Выбрать
инструмент «Конус»;

2)     
Отметить две
точки на оси Oz;

3)     
В открывшемся
окне ввести радиус конуса (см. рис. 7)

 

                                                                         

                                              Рис.6                                                                      Рис.7

Инструмент «Сфера по центру и
точке» позволяет построить сферу по ее центру и точке, лежащей на сфере.
Для того, чтобы построить сферу по центру и точке, необходимо:

1)     
Выбрать
инструмент «Сфера по центру и точке»;

2)     
Отметить центр
сферы;

3)     
Отметить вторую
точку, которая лежит на сфере (см. рис.

Инструмент «Сфера по центру и
радиусу» позволяет построить сферу по ее центру и радиусу. Для того, чтобы
построить сферу по центру и радиусу, необходимо:

1)     
Выбрать
инструмент «Сфера по центру и радиусу»;

2)     
Отметить центр
сферы;

3)     
В открывшемся
окне ввести радиус сферы (см. рис. 9)

                                   

                                              Рис.8                                                                      Рис.9

§3. Решение задач в Geogebra 3D Calculator

Задачи 1-6 выполните самостоятельно, используя
вышеприведенные алгоритмы.

Задача 1. Постройте пятиугольную пирамиду по алгоритму.

Задача 2. Постройте треугольную призму по алгоритму.

Задача 3. Постройте цилиндр с радиусом 3 по алгоритму.

Задача 4. Постройте конус с радиусом 2 по алгоритму.

Задача 5. Постройте сферу по центру и точке, лежащей на сфере. Задача 6.
Постройте сферу по центру и радиусу (𝑟 = 3).

Задача 7. Постройте треугольную пирамиду 𝐷𝐴𝐵𝐶. На ребрах 𝐴𝐵,
𝐵𝐷 и 𝐶𝐷 отметьте точки

𝑀,
𝑁 и 𝑃
соответственно. Постройте сечение тетраэдра плоскостью 𝑀𝑁𝑃 (рис.10)

Решение. Проведем прямые 𝑀𝑁 и 𝑁𝑃 (рис.11). Для наглядности повращайте
3D полотно.

Построим прямую 𝐵𝐶 и найдем точку 𝐸 – точку пересечения прямых 𝐵𝐶
и 𝑁𝑃 (рис.12)

Точки 𝐸 и 𝑀 лежат в одной плоскости. Проведем
прямую 𝐸𝑀 (рис.13)

Точка 𝐹 – точка пересечения прямых 𝐸𝑀 и 𝐴𝐶. (рис. 14)

Точки 𝐹 и 𝑃 лежат в одной плоскости. Проведем
прямую 𝐹𝑃 (рис. 15)

Итак, четырехугольник FPMN – искомое сечение. Далее можно изменить
стиль линий, заливку пирамиды и т.д. (рис.16) 

 

                                             Рис. 10                                                                   Рис.
11

 

                                            Рис. 12                                                                   Рис.
13

 

                                            Рис. 14                                                                   Рис.
15

 

Рис. 16

Преимущество Geogebra 3D Calculator также
состоит в том, что всегда можно проверить, правильно ли сечение было построено.

Для того, чтобы проверить
правильность построенного сечения, необходимо выбрать инструмент «Плоскость по
трем точкам» и выбрать три точки (в задаче 7 это точки 𝑀,
𝑁 и 𝑃.

 

Рис. 17

Задача 8. Точка 𝑀 лежит на боковой грани 𝐴𝐵𝐷 тетраэдра 𝐷𝐴𝐵𝐶. Построить сечение тетраэдра
плоскостью, проходящей через точку 𝑀, параллельно основанию 𝐴𝐵𝐶. (рис. 18 а,б)

 

                                                а)                                                                           б)

Рис.18

ГЛАВА III. ПРИМЕНЕНИЕ GEOGEBRA НА
УРОКАХ АЛГЕБРЫ

§1. Знакомство с интерфейсом

Задача 1. Построить график функции 𝑦 = 3𝑥 + 2

В поле ввода ввести 𝑦
= 3𝑥 + 2 и нажать клавишу Enter.

 

У нас получилась прямая

 

Подпишем график.

Для этого переключимся на Панель инструментов
«Геометрия»

Нажимаем кнопку LaTeX формула.

Кликаем мышкой в поле ввода. Теперь можно написать 𝑦 = 3𝑥 + 2 и
жмем кнопку OK.

 

Если надпись кажется мелкой, то можно увеличить ее
размер. Для этого на Панели инструментов нужны кликнуть по кнопке «Стрелка».

 

Теперь кликнем по надписи, которую мы только что
сделали. У вас появится вспомогательная панель для работы с текстом. Здесь
можно изменить цвет надписи, придать ей форматирование (курсив, жирный) и
изменить размер. Для этого кликаем по кнопке «тТ» и выбираем тот размер,
который хотим. 

 

Например, «Большой»

 

Задача 2. Построим график функции 𝑦 = 𝑥² + 2.

Переходим обратно на панель ввода формул

На полотне до сих пор
остались прямая и надпись. Можете их убрать. 

Для этого возвращаемся на панель инструментов.

Посмотрите,

рядом с каждой формулой есть цветной кружочек. Чтобы
сделать рисунок невидимым, вам нужно один раз нажать на него, чтобы он
превратился в окружность.

Вот так теперь выглядит панель инструментов.

 

А вот так выглядит сам график. Не забудьте его
подписать.

 

Задача 3. Построить график функции 𝑦 = ³

𝑥

Чтобы построить график обратной
пропорциональности, нам понадобиться ввод дроби. Вводим y=3/x и жмем клавишу
Enter.

 

Задание 4. Построить график
функции 𝑦 = 𝑥²
− 3|𝑥| − 𝑥 и определить, при каких значениях 𝑎 прямая 𝑦 = 𝑎 имеет с
графиком три общие точки.

Рассмотрим два случая, когда 𝑥 ≥ 0 и 𝑥 < 0.

При 𝑥 ≥ 0 имеем 𝑦 = 𝑥² − 3𝑥
− 𝑥 ⇔ 𝑦 = 𝑥² − 4𝑥.

При 𝑥 < 0 имеем 𝑦 = 𝑥² + 3𝑥
− 𝑥 ⇔ 𝑦 = 𝑥² + 2𝑥.

𝑥²
− 4𝑥, если 𝑥 ≥ 0, Составим кусочно-заданную
функцию 𝑦 = {𝑥₂
+ 2𝑥, если 𝑥 < 0.

Ну а теперь построим график этой функции.

Все, что нам было построено до этого
можно скрыть (смотри задание №2), либо удалить. Для этого просто нажимаем на
три точки возле надписи в поле ввода:

Выбираем пункт «Удалить».

Итак, приступим к построению.

Как вы видите, у нас
есть две функции и два условия. Чтобы ввести их нам понадобиться специальная
операция условия. В поле ввода пишем: Если()

 

А теперь нужно записать то, что мы
хотим построить. Для начала построим ту часть графика, которая выполняется при
условии 𝑥 ≥ 0.

Ставим курсор между скобок и набирает следующий
текст

𝑥
>= 0, 𝑥² − 4𝑥

и нажимаем клавишу Enter. Вот то, что в итоге
получится в поле ввода

 

А вот и сам график 

 

Осталось построить вторую часть функции.

Вводим: Если(𝑥
< 0, 𝑥² + 2𝑥) и жмем клавишу Enter.

И итоге получаем график функции.

 

Теперь разберемся с функцией 𝑦 = 𝑎. Это
линейная функция, ее графиком является прямая, параллельная оси 𝑥.

Однако, значение параметра 𝑎 нам не дано. Поэтому
вместо 𝑎 может
быть абсолютно любое число. Как это показать в программе Geogebra?

И тут нам снова нужно перейти на панель «Геометрия»
(смотри задание №1).

Выбираем кнопку «Ползунок».

Теперь в любом месте координатной
плоскости кликаем мышкой. Откроется новое окно, где можно выставить параметры
для ползунка.

 

Оставим все так, как есть и нажмем кнопку ОК. 

Вот что в итоге у нас получилось.

 

Возвращаемся на панель инструментов
«Алгебра» и вводим 𝑦 = 𝑎.
Жмем клавишу Enter. Появилась прямая.

Теперь
вместо 𝑎 у нас
будет стоять то значение, которое задается по умолчанию, т.е.

1.

 

Осталось запустить анимацию, чтобы
наглядно продемонстрировать, при каких значениях a сколько будет точек
пересечения. Для запуска анимации нажмите значок «Треугольник» рядом с
ползунком на панели ввода. Прямая начнем двигать вверх и вниз.

Нам нужно было определить, при каких
значениях 𝑎
прямая 𝑦 = 𝑎
имеет с графиком данной функции три общих точки.

А можно ли было обойтись без кусочно-заданной
функции? Конечно, можно было.

Для этого нам всего лишь нужно
было правильно ввести формулу, содержащую модуль  𝑦 = 𝑥² − 3|𝑥| − 𝑥.

Знак модуля можно ввести разными способами.

1.      Просто
набрать 𝑦 = 𝑥²
− 3 ∗ |𝑥| − 𝑥 с клавиатуры.

2.      Набрать
𝑦 = 𝑥² −
3 ∗ |𝑥| − 𝑥, используя значок «модуль» на нижней панели
инструментов.

3.      Набрать
𝑦 = 𝑥² −
3 ∗ 𝑎𝑏𝑠(𝑥) − 𝑥, где 𝑎𝑏𝑠 –
это функция, задающая модуль.

Задание 1.

Построить графики функций на одном чертеже:

 

GeoGebra — самая популярная в мире бесплатная математическая программа. С помощью обучающей программы по математике, можно будет выполнить множество полезных вещей: анализировать функции, строить графики, решать задачи, работать с функциями и т. д.

Интерфейс программы GeoGebra (ГеоГебра) напоминает классную доску, на которой можно рисовать графики, создавать геометрические фигуры и т. п. В окне программы будет наглядно отображены производимые изменения: если вы измените уравнение, кривая перестроится, изменится масштаб или ее положение в пространстве, уравнение, написанное рядом с кривой, автоматически будет скорректировано, согласно новым значениям.

Программу GeoGebra широко используют в мире миллионы пользователей для обучения алгебре и геометрии. Процесс обучения нагляден благодаря визуальной форме использования приложения.

Возможности программы по математике не ограничиваются только построением графиков, программу GeoGebra можно будет использовать для интерактивных чертежей при решении геометрических задач. Программа ГеоГебра обладает мощными и функциональными возможностями, которые позволяет наглядно и просто обучаться математике.

Приложение включает в себя геометрию, алгебру, есть возможность совершать арифметические операции, создавать таблицы, графики, возможна работа со статистикой, работа с функциями, поддерживается создание анимации и т. д. В программе GeoGebra можно будет создавать различные 2D и 3D фигуры, интерактивные ролики, которые затем можно будет размещать в интернете.

Все приложения, входящие в состав программы GeoGebra, доступны и синхронизируются между собой для работы в составе одного пакета.

GeoGebra была создана Маркусом Хохенвартером. Программа написана на языке Java, приложение поддерживает работу в различных операционных системах: Windows, Mac OS X, Linux, Android.

С сайта производителя можно будет скачать обычную версию программы GeoGebra для установки на компьютер. Также можно будет скачать переносную версию программы (GeoGebra Portable) для соответствующей операционной системы.

GeoGebra скачать

После запуска GeoGebra на компьютере, ознакомимся с интерфейсом программы.

Интерфейс GeoGebra

Интерфейс программы GeoGebra напоминает графический редактор. Программу можно использовать для черчения, но это не основное предназначение приложения.

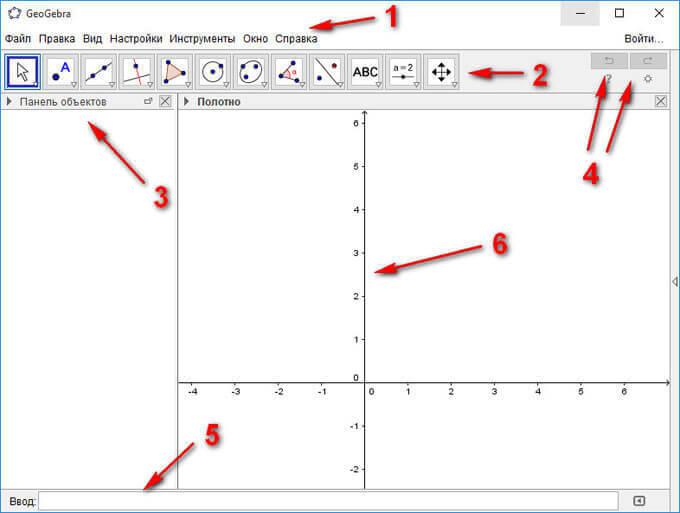
Давайте рассмотрим основные элементы интерфейса программы GeoGebra:

1. Полоса меню. Из меню вы можете изменить настройки программы.
2. Панель инструментов. Здесь находятся инструменты для создания объектов. После щелчка по треугольнику в правом нижнем углу кнопки, будут открыты дополнительные инструменты. Операции, доступные в панели инструментов, можно производить с помощью строки ввода.
3. Панель объектов. В Панели объектов отображаются введенные переменные и функции. Вместо имен переменных здесь отображаются их значения. Для того, чтобы увидеть формулу в символьном виде, нужно будет кликнуть по ней правой кнопкой мыши.
4. Кнопки «Отменить» и «Повторить».
5. Строка ввода. Это основной инструмент при работе в программе GeoGebra. Здесь вводятся команды и формулы, задаются значения переменных. Справа от строки ввода расположена кнопка «Список команд». С помощью дополнительных команд можно будет вводить команды и отсутствующие на клавиатуре символы.
6. Рабочая область. Все построения в программе производятся в рабочей области. Вы можете изменить масштаб с помощью колесика мыши, перемещать по рабочей области ось координат.

Далее попытаемся выполнить некоторые элементарные действия в программе GeoGebra.

Построение графика функции в GeoGebra

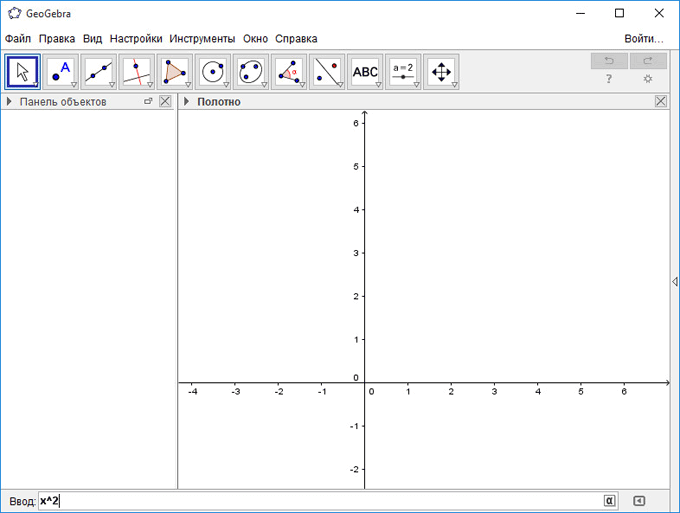
Для построения графика функции достаточно будет набрать ее в поле ввода. Для отображения параболы нужно будет написать в строке «Ввод» следующее выражение:

x^2

Символ «^» в программе GeoGebra обозначает возведение в степень.

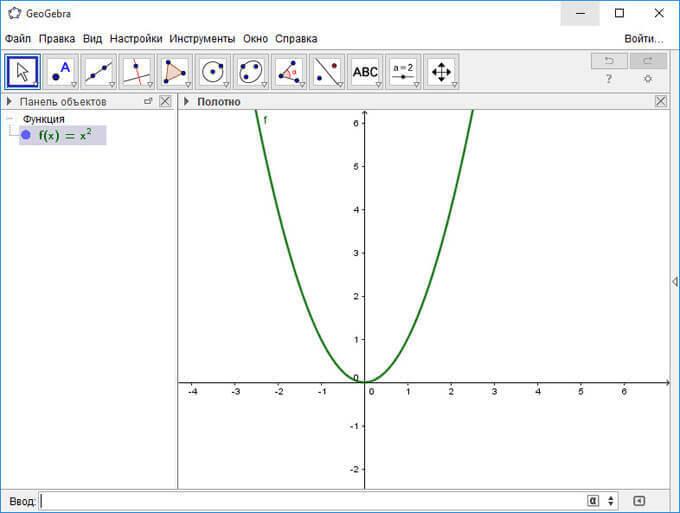
Далее нажмите на кнопку «Enter». После этого в рабочей области будет построен график. Рисунок можно будет масштабировать с помощью колесика мыши. Для перемещения рабочей области нужно будет нажать на клавишу «Shift», одновременно удерживая нажатой левую кнопку мыши.

Вы можете перемещать сам график при помощи нажатой правой кнопки мыши, при этом, в Панели объектов будут отображены изменения в уравнении.

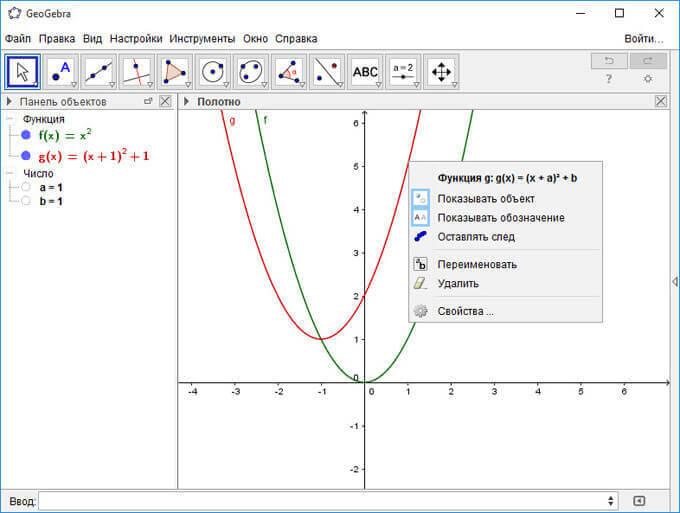
Вы можете добавить в уравнение переменные параметры, например, следующие (введите их строку ввода поочередно):

a=1
b=1
(x+a)^2+b

В рабочей области появится еще одна парабола, смещенная влево на одну единицу. Кликнув по графику, вы можете из открывшегося контекстного меню производить необходимые действия.

Создание треугольника в GeoGebra

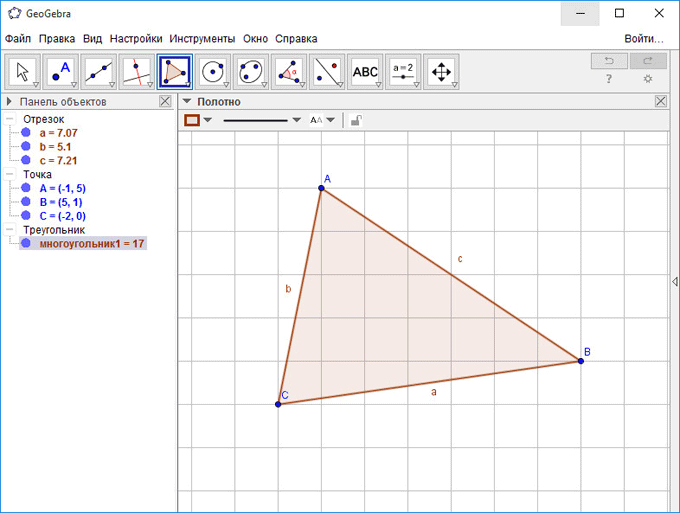
Давайте попробуем начертить треугольник в программе GeoGebra. Для этого нужно будет перейти в «геометрический» режим для того, чтобы включить отображение сетки, и отключить отображение оси координат.

Кликните правой кнопкой мыши по оси координат, в контекстном меню выберите пункт «Сетка», а затем там кликните по пункту «Оси» для отключения оси координат. На панели инструментов нажмите на кнопку «Многоугольник».

После этого нарисуйте треугольник, последовательно установив три вершины. При необходимости, вы можете ввести точные координаты. Для этого вам нужно будет кликнуть по точке правой кнопкой мыши.

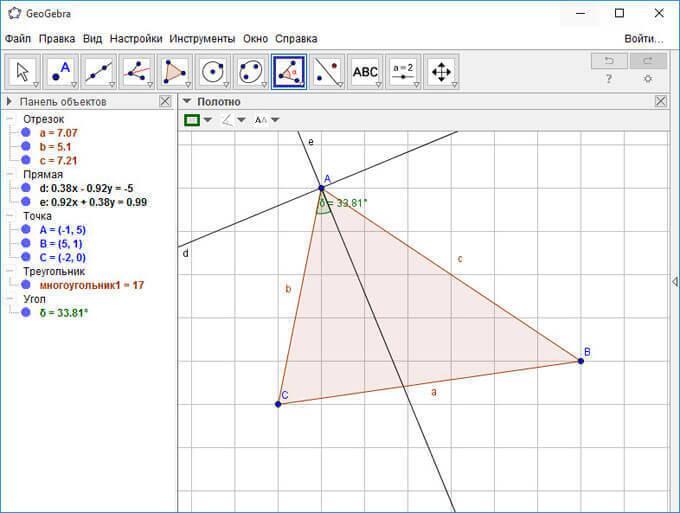
Далее вы можете создать биссектрису угла. Для этого нажмите на треугольную кнопку под кнопкой «Перпендикулярная прямая», а затем выберите из выпадающего списка инструмент «Биссектриса угла». После этого, кликните по двум отрезкам образующих угол, биссектриса будет создана.

Вы можете обозначить угол. Для этого нажмите на кнопку инструмента «Угол» в Панели инструментов. Для отображения интересующего вас угла выберите три точки или две прямые.

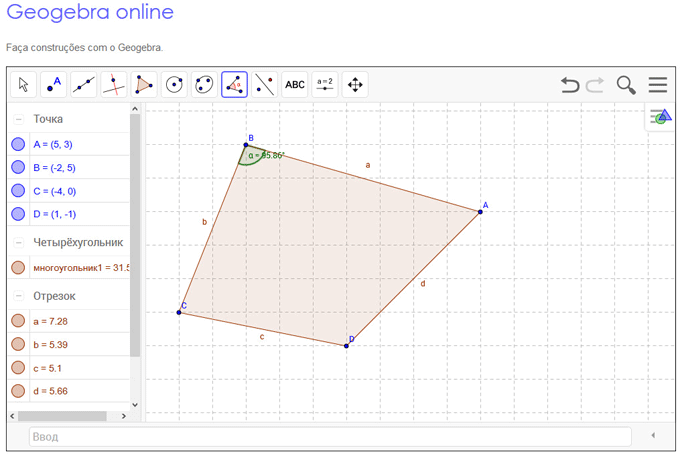
Geogebra online

У программы GeoGebra имеется онлайн версия: Geogebra online (ГеоГебра онлайн). После перехода на сайт www.geogebra.org, вы можете открыть программу GeoGebra в своем браузере для выполнения необходимых действий. Таким образом, даже не устанавливая программу GeoGebra на свой компьютер, при наличии интернета, вы можете работать в этой математической программе, войдя на онлайн сервис со своего мобильного устройства.

Расширение GeoGebra

Создано расширение GeoGebra для браузера Google Chrome. Обратите внимание на количество пользователей расширения: более 2.6 миллиона человек. Немногие расширения из магазина Chrome могут сравниться с такими цифрами. Это свидетельствует о том, что приложение GeoGebra широко используется в мире для образовательных целей.

Для входа в расширение кликните по кнопке «Сервисы» на панели закладок в браузере Google Chrome. После этого будет открыто окно расширения GeoGebra в вашем браузере. На начальном экране вы можете выбрать раздел математики, с которым далее вы будете работать в приложении.

Дополнительные материалы по работе в программе, вы можете найти на сайте производителя приложения, и в интернете.

Выводы статьи

Бесплатная программа GeoGebra предназначена для обучения математике. С помощью программы GeoGebra (ГеоГебра) можно обучаться или работать в динамической математической среде, включающей в себя геометрию, алгебру, другие разделы, с широкими функциональными возможностями.